交叉跨链系统
交叉跨链与化身资产,是实现多个异构公链生态进行主动融合互通的最直接有效方式。?在过往,单一公链一直无法突破自身生态边界,即便引入当下诸多跨链手段,依然属于被动式映射主流资产,用户并不会主动随着资产映射而来,生态规模依然拘束于自身公链上应用场景的丰富度和接受度;映射资产再优质却无法再次流通,用户缺乏在不同公链应用间自由切换实施套利以及获取资产的最短路径,自身公链生态也就无法被更大公链的生态、应用和用户所主动接纳;跨链映射的主流资产成为“一潭死水”,跨链也就成了伪命题,自身公链生态的边界依然无法打破,用户和应用得不到增量式增长。?拓宽自身公链生态的边界,打造应用“出圈”和新用户“入圈”,生态有界,应用有边,但资产无形,着力建设一种新的生态维度——“化身资产”,即在完成主流资产跨入映射的同时,建立起映射资产在不同公链生态间的自由进出和共享,让化身资产随着应用需求自由流转于目标公链,同时为“新维度”建立起移动坐标轴——“交叉跨链系统”,一种更为强悍而普适的跨链体系,可以让化身资产自由穿梭在多个不同公链间,使多种公链的应用生态发生折叠。?MOV 交叉跨链系统,是基于 OFMF 框架建设的一个无准入(permission-less)拜占庭容错分布式网络系统,构建在多种公链体系之上的通用协议层服务,并不专属于 MOV 体系。其核心功能升级为通过安全多方计算(sMPC)和共识算法协调所有 Fednodes 进行跨链资产的去中心化安全托管和转移,以及跨链交易的解析和执行。Fednodes 是更为开放的联邦节点,是交叉跨链系统的核心角色,为分布式网关网络贡献 CPU 和存储,准确执行安全多方计算程序,任何生态的任何角色都可以通过抵押成为 Fednodes。?交叉跨链系统最引入注目的创新是,改变以往跨链系统单一的资产流向,升级为主动式全链接跨入网络。假定 MOV 交叉跨链系统底层适配了 ETH、BTC、BTM、Polkadot 四种公链体系,目前是其他三种公链上的资产被动式向 BTM 生态迁徙,并在 BTM 生态寻找应用的场景,最终生命周期将在 BTM 生态终止,重新被提取回原始公链。在交叉式跨链系统的支持下,BTM 上的资产,不论是 BTM 原生生态资产还是从其他公链跨入的化身资产,都可以主动式进入到任何其他三种公链体系,去拓宽自己的应用场景。?OFMF 框架实行“多签+门限”的托管方案,交叉跨链系统将更为广泛地实施基于安全多方计算的门限签名托管方案。所有成为 Fednodes 的节点共同组成一个分布式的多方计算网络,由拜占庭容错共识算法调控系统的 liveness 和 safety,确保多方计算程序可以持续运行。Fednodes 节点定期选举产生,进行权力的每届更迭。得益于抵押型共识系统的引入,快速更迭 Fednodes 可以在交叉跨链系统中成为现实,真正走向完全开放式的联邦网关网络,这也极大提升了联邦见证的系统效率和灵活性,使跨链体验更为迅速和安全。Fednodes 的抵押资产也给跨链系统带来更为可靠的安全边际。?
跨链交易类型
在打通 BTC、BTM、ETH 三种公链体系的交叉跨链系统中,一共存在五种跨链交易类型(可归结为三大类):(1)将 BTC 资产从 BTC 主网发送到 BTM 生态(Type 1:锁定——铸币)(2)将 BTM 生态的 BTC 资产提取到 BTC 主网(Type 2:燃烧——释放)(3)将 BTM 生态的 BTC 资产提取到 ETH 主网(Type 3:燃烧——铸币)(4)将 ETH 主网上的 BTC 资产提取到 BTM 生态(Type 3:燃烧——铸币)(5)将 ETH 主网上的 BTC 资产提取到 BTC 主网(Type 2:燃烧——释放) ?我们把这种全链接式的跨链方式称为交叉跨链。交叉跨链拥有以下四个深远意义:(a)BTC资产可以在多个公链生态体系内无缝切换,随应用而流转,让小生态公链体系可以与大生态公链体系重合,获得更多用户和流量,而大生态公链体系可以捕获更为强悍的二层网络和化身资产;(b)定义可编程跨链时代的来临。交叉跨链也是一个分布式系统,拥有抵押治理和共识容错,它可以灵活解析来自用户发起的任何类型的跨链交易,包括方向、数量、附加数据和更为具体的指令,比如跨链切分、部分延迟、条件式触发等;(c)发展成为一种被广泛接受的统一跨链标准、协议层;(d)发掘最优跨链路径和最优化身资产。
可编程跨链网关?
用户可在交叉跨链系统界面自由定义一组跨链交易的脚本:(1)一笔锁定资产向不同公链铸币,数量、时间、映射地址都可以设定;(2)一笔锁定资产,先定义向公链 A 铸币,再定义将 A 的铸币燃烧,并在公链 B 上铸币;(3)一笔锁定资产,延迟触发。?可以让一笔资产彻底无法追踪,可以实现事件驱动的跨链。?
联邦分布式系统
分布式系统的必要性?跨链网关系统最高效的实现是见证人机制,OFMF 在见证人机制的基础上将网关节点进一步开放出去,以寻求去中心化的权力构成,符合一个公链生态扩大自身规模的愿景。但见证人机制的性能瓶颈受制于两方面,一是所链接的两条公链上原生交易的确认速度,二是见证人系统自身的决策效率。前者没有太大优化空间,后者的瓶颈可以进一步拆分成两种:(i)见证人共同执行跨链签名的效率;(ii)见证人重组的效率。?最理想的跨链网关系统是一个可以主动获取可靠原始验证数据并自主进行分布式决策的自动化网络,并不需要人工去操纵跨链签名的合法性判断和生成,能够引入成熟机密信息管理保管在线秘密和密钥,能够迅速主动捕获两公链上随时发生的跨链事件并建立存储,然后在判断交易合法性的前提下进行安全多方计算快速生成跨链交易签名,依靠分布式容错共识算法自动去除恶意节点的干扰,依托门限签名节省多方签名的费用成本和时间成本,尤其是在网关网络规模不断扩大走向更为开放的进程中,效用更为显著。MOV 交叉跨链系统也是在 OFMF 框架上升级为完全分布式网络系统,更大程度的利用安全多方计算和共识算法决策的性质,来提升整个跨链网关的效率和安全。?由 Fednodes 组成的分布式系统,每周期换届选举出新的决策 Fednodes 节点集合,跟一条链系统有着本质的相似,但没有资产和账户体系,没有转账交易,只对跨链事件进行共识见证,并协作执行门限签名进行铸币、燃烧和释放等操作,能够准确解析用户的每一笔跨链交易请求或者脚本。?由于交叉跨链系统的无准入特性,以及门限签名的合成是一个多方在线交互验证的分布式协作过程,当存在未知数量的恶意节点或者网络出现分区的情况下,可能无法就某一笔跨链交易进行共识验证并生成合法的门限签名,导致网关网络的阻塞或者被攻击,影响跨链系统的效率以及安全性。针对每一笔跨链请求,Fednodes 需要能够就跨链请求序列(包括交叉跨链系统记录的请求序列以及跨链交易在链上被打包区块并确认的序列)、跨链请求的正确性(类似区块链上的转账交易的正确性)达成一致,并且对每一笔合法跨链请求执行(execute)安全多方计算过程,该过程依然是一个依托共识网络完成门限签名的过程,确保在有限时间内完成合法门限签名的签署和执行。?sMPC 过程涉及多次(并发/多轮)随机秘密份额的分布式生成与交互验证(DKG/VSS/RNG/arithmetic operation/inverse/multiplicativ-to-additive),是实现多方安全计算的核心,并且处于异步网络通信环境里,延迟不可预测,另外恶意节点会对节点间份额集合的一致性进行干扰攻击,例如恶意节点给一部分诚实节点一种秘密份额子集,但是给另一部分诚实节点另外一种子集,在缺乏多轮交互确认以及可靠广播信道的系统里这种行为极具破坏性。因此 Fednodes 的分布式网络应该是一种拜占庭容错的一致性系统,即便阈值范围内的节点出现 slow/fault/failure/crash 或者 Byzantine 行为,也不妨碍系统继续完成协作,否则整个系统的效率将极大被阻塞影响。这种拜占庭容错系统可以更细分为 replicated state machines 和 Byzantine quorum systems 两种。后者一般适用于只涉及读和写等简单的语义,基于前者 MOV 交叉跨链系统将实现一种契合安全多方计算过程的 Asynchronous Byzantine Broadcast Protocols,用于消息(见证跨链事件/安全多方计算门限签名)的防拜占庭可靠传输,并灵活适配于各种网络模型(同步网络/半同步网络)。??Reliable Broadcast?我们构建?Reliable broadcast(RBC),一种针对拜占庭将军问题的广播模型,满足下面特性:?
Validity:如果一个诚实节点广播(r-broadcast)一条消息 <ID.j.s, m>,那么所有的诚实节点都将收到(r-deliver)同样的消息。Consistency:如果一些诚实节点 r-deliver 了消息 <ID.j.s, m>,另一些诚实节点 r-deliver 了消息 <ID.j.s, m′>,那么 m = m′。Totality:如果一些诚实节点 r-deliver 了序号为 ID.j.s 的消息,那么所有的诚实节点都将 r-deliver 同样序号的消息。Integrity:每个诚实节点只能 r-deliver 最多一条 ID.j.s 标识下的消息 m。Efficiency:每个 D.j.s 序号下的 broadcast 实例的通信复杂度都是 uniformly bounded。
Validity 保证了算法的 liveness,Consistency 和 Totality 是对传统定义 agreement 的拆分,拆分的缘由之一是不保证 totality 的 reliable broadcast 也是一 种有用的方法。?基于此我们构建协议如下 ——(1)当收到消息 (ID.j.s, in, r-broadcast, m),执行: ?我们把这种全链接式的跨链方式称为交叉跨链。交叉跨链拥有以下四个深远意义:(a)BTC资产可以在多个公链生态体系内无缝切换,随应用而流转,让小生态公链体系可以与大生态公链体系重合,获得更多用户和流量,而大生态公链体系可以捕获更为强悍的二层网络和化身资产;(b)定义可编程跨链时代的来临。交叉跨链也是一个分布式系统,拥有抵押治理和共识容错,它可以灵活解析来自用户发起的任何类型的跨链交易,包括方向、数量、附加数据和更为具体的指令,比如跨链切分、部分延迟、条件式触发等;(c)发展成为一种被广泛接受的统一跨链标准、协议层;(d)发掘最优跨链路径和最优化身资产。
可编程跨链网关?
用户可在交叉跨链系统界面自由定义一组跨链交易的脚本:(1)一笔锁定资产向不同公链铸币,数量、时间、映射地址都可以设定;(2)一笔锁定资产,先定义向公链 A 铸币,再定义将 A 的铸币燃烧,并在公链 B 上铸币;(3)一笔锁定资产,延迟触发。?可以让一笔资产彻底无法追踪,可以实现事件驱动的跨链。?
联邦分布式系统
分布式系统的必要性?跨链网关系统最高效的实现是见证人机制,OFMF 在见证人机制的基础上将网关节点进一步开放出去,以寻求去中心化的权力构成,符合一个公链生态扩大自身规模的愿景。但见证人机制的性能瓶颈受制于两方面,一是所链接的两条公链上原生交易的确认速度,二是见证人系统自身的决策效率。前者没有太大优化空间,后者的瓶颈可以进一步拆分成两种:(i)见证人共同执行跨链签名的效率;(ii)见证人重组的效率。?最理想的跨链网关系统是一个可以主动获取可靠原始验证数据并自主进行分布式决策的自动化网络,并不需要人工去操纵跨链签名的合法性判断和生成,能够引入成熟机密信息管理保管在线秘密和密钥,能够迅速主动捕获两公链上随时发生的跨链事件并建立存储,然后在判断交易合法性的前提下进行安全多方计算快速生成跨链交易签名,依靠分布式容错共识算法自动去除恶意节点的干扰,依托门限签名节省多方签名的费用成本和时间成本,尤其是在网关网络规模不断扩大走向更为开放的进程中,效用更为显著。MOV 交叉跨链系统也是在 OFMF 框架上升级为完全分布式网络系统,更大程度的利用安全多方计算和共识算法决策的性质,来提升整个跨链网关的效率和安全。?由 Fednodes 组成的分布式系统,每周期换届选举出新的决策 Fednodes 节点集合,跟一条链系统有着本质的相似,但没有资产和账户体系,没有转账交易,只对跨链事件进行共识见证,并协作执行门限签名进行铸币、燃烧和释放等操作,能够准确解析用户的每一笔跨链交易请求或者脚本。?由于交叉跨链系统的无准入特性,以及门限签名的合成是一个多方在线交互验证的分布式协作过程,当存在未知数量的恶意节点或者网络出现分区的情况下,可能无法就某一笔跨链交易进行共识验证并生成合法的门限签名,导致网关网络的阻塞或者被攻击,影响跨链系统的效率以及安全性。针对每一笔跨链请求,Fednodes 需要能够就跨链请求序列(包括交叉跨链系统记录的请求序列以及跨链交易在链上被打包区块并确认的序列)、跨链请求的正确性(类似区块链上的转账交易的正确性)达成一致,并且对每一笔合法跨链请求执行(execute)安全多方计算过程,该过程依然是一个依托共识网络完成门限签名的过程,确保在有限时间内完成合法门限签名的签署和执行。?sMPC 过程涉及多次(并发/多轮)随机秘密份额的分布式生成与交互验证(DKG/VSS/RNG/arithmetic operation/inverse/multiplicativ-to-additive),是实现多方安全计算的核心,并且处于异步网络通信环境里,延迟不可预测,另外恶意节点会对节点间份额集合的一致性进行干扰攻击,例如恶意节点给一部分诚实节点一种秘密份额子集,但是给另一部分诚实节点另外一种子集,在缺乏多轮交互确认以及可靠广播信道的系统里这种行为极具破坏性。因此 Fednodes 的分布式网络应该是一种拜占庭容错的一致性系统,即便阈值范围内的节点出现 slow/fault/failure/crash 或者 Byzantine 行为,也不妨碍系统继续完成协作,否则整个系统的效率将极大被阻塞影响。这种拜占庭容错系统可以更细分为 replicated state machines 和 Byzantine quorum systems 两种。后者一般适用于只涉及读和写等简单的语义,基于前者 MOV 交叉跨链系统将实现一种契合安全多方计算过程的 Asynchronous Byzantine Broadcast Protocols,用于消息(见证跨链事件/安全多方计算门限签名)的防拜占庭可靠传输,并灵活适配于各种网络模型(同步网络/半同步网络)。??Reliable Broadcast?我们构建?Reliable broadcast(RBC),一种针对拜占庭将军问题的广播模型,满足下面特性:?
Validity:如果一个诚实节点广播(r-broadcast)一条消息 <ID.j.s, m>,那么所有的诚实节点都将收到(r-deliver)同样的消息。Consistency:如果一些诚实节点 r-deliver 了消息 <ID.j.s, m>,另一些诚实节点 r-deliver 了消息 <ID.j.s, m′>,那么 m = m′。Totality:如果一些诚实节点 r-deliver 了序号为 ID.j.s 的消息,那么所有的诚实节点都将 r-deliver 同样序号的消息。Integrity:每个诚实节点只能 r-deliver 最多一条 ID.j.s 标识下的消息 m。Efficiency:每个 D.j.s 序号下的 broadcast 实例的通信复杂度都是 uniformly bounded。
Validity 保证了算法的 liveness,Consistency 和 Totality 是对传统定义 agreement 的拆分,拆分的缘由之一是不保证 totality 的 reliable broadcast 也是一 种有用的方法。?基于此我们构建协议如下 ——(1)当收到消息 (ID.j.s, in, r-broadcast, m),执行: (广播/r-send)?(2)当节点收到来自 Leader 节点 Pι 的消息 (ID.j.s, r-send, m),执行: (广播/r-send)?(2)当节点收到来自 Leader 节点 Pι 的消息 (ID.j.s, r-send, m),执行: (广播/r-echo/第一阶段)?(3)当节点收到来自其他节点的消息 (ID.j.s, r-echo, d): (广播/r-echo/第一阶段)?(3)当节点收到来自其他节点的消息 (ID.j.s, r-echo, d): (满足阈值后广播/r-ready/第二阶段)?(4)当节点收到来自其他节点的消息 (ID.j.s, r-ready, d): (满足阈值后广播/r-ready/第二阶段)?(4)当节点收到来自其他节点的消息 (ID.j.s, r-ready, d): (满足拜占庭容错阈值后输出/r-deliver/第三阶段)?(*)在收到消息 (ID.j.s, r-request) 后执行: (满足拜占庭容错阈值后输出/r-deliver/第三阶段)?(*)在收到消息 (ID.j.s, r-request) 后执行: (获取最新消息内容/r-answer)?? (获取最新消息内容/r-answer)?? ??RBC 传承了经典拜占庭容错共识的三阶段,同时引入了更为可靠的消息传输,十分适合安全多方计算网络的秘密份额传输和合成。Reliable broadcast 分为 “echo” 和 “ready” 两个关键阶段,echo 阶段保证每个节点都 accept 到了同样的消息(consistency),ready 阶段保证如果一个人 accept 了一条消息 M,那么其他所有节点也都 accept 了 M(reliability)。?整体上消息复杂度是 O(N^2)。如果没有 fault 出现,复杂度可降为: ??RBC 传承了经典拜占庭容错共识的三阶段,同时引入了更为可靠的消息传输,十分适合安全多方计算网络的秘密份额传输和合成。Reliable broadcast 分为 “echo” 和 “ready” 两个关键阶段,echo 阶段保证每个节点都 accept 到了同样的消息(consistency),ready 阶段保证如果一个人 accept 了一条消息 M,那么其他所有节点也都 accept 了 M(reliability)。?整体上消息复杂度是 O(N^2)。如果没有 fault 出现,复杂度可降为: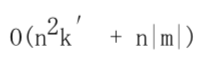 注:m 是发送的消息,k′ 是 hash 的长度。但是需要注意的是恶意攻击者会阻塞 r-send 过程导致开销增大。?
安全多方计算
门限 ECDSA 签名?近些年来人们在不断追寻更为通用和灵活的 (t, n) 门限方案,即 n >= t+1,且只需要 t+1 方即可完成签名。但是更多的阻碍出现在了分布式密钥生成协议(DKG)上,往往都是极具消耗性的,难以用于实际生产。?在通用的 DSA 签名算法中,假设循环群 G 由素数阶 q 和基点 g 来定义,密钥(secret key) x 统一从以素数 q 为模数的有限域 Z/q 中随机选取,从 Z/q 中随机选取 k。对 DSA 门限签名的实现难度在于需要多方共同来计算 R(涉及 g 求幂和 k 求反操作)和 s(涉及两个秘密值 k 和 x 的乘操作),这种非线性的计算对多方安全计算来说是十分困难的。[1] 受到著名的 MPC 实现 SPDZ [2] 的启发,采用了一种不同的多方计算法:假设有两个秘密值 a 和 b 在多方之间分享,有 a = a1+...+an,b = b1+...+bn,对于参与方 Pi 拥有 ai 和 bi;此时我们需要生成 c = ab 的分享,注意到有 注:m 是发送的消息,k′ 是 hash 的长度。但是需要注意的是恶意攻击者会阻塞 r-send 过程导致开销增大。?
安全多方计算
门限 ECDSA 签名?近些年来人们在不断追寻更为通用和灵活的 (t, n) 门限方案,即 n >= t+1,且只需要 t+1 方即可完成签名。但是更多的阻碍出现在了分布式密钥生成协议(DKG)上,往往都是极具消耗性的,难以用于实际生产。?在通用的 DSA 签名算法中,假设循环群 G 由素数阶 q 和基点 g 来定义,密钥(secret key) x 统一从以素数 q 为模数的有限域 Z/q 中随机选取,从 Z/q 中随机选取 k。对 DSA 门限签名的实现难度在于需要多方共同来计算 R(涉及 g 求幂和 k 求反操作)和 s(涉及两个秘密值 k 和 x 的乘操作),这种非线性的计算对多方安全计算来说是十分困难的。[1] 受到著名的 MPC 实现 SPDZ [2] 的启发,采用了一种不同的多方计算法:假设有两个秘密值 a 和 b 在多方之间分享,有 a = a1+...+an,b = b1+...+bn,对于参与方 Pi 拥有 ai 和 bi;此时我们需要生成 c = ab 的分享,注意到有 需要对每一项秘密值 aibj 都进行分享;这给予的启示是,可以让参与方们根据各自拥有的 a 和 b 的秘密份额两两配对组合生成秘密值 aibj,基于此创建一种简单而又优雅的门限 ECDSA 协议。根据上面提到的原理计算乘法分享:? 需要对每一项秘密值 aibj 都进行分享;这给予的启示是,可以让参与方们根据各自拥有的 a 和 b 的秘密份额两两配对组合生成秘密值 aibj,基于此创建一种简单而又优雅的门限 ECDSA 协议。根据上面提到的原理计算乘法分享:?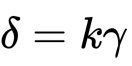  因此可以获得 R 的多方计算: 因此可以获得 R 的多方计算: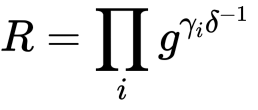 签名的 s 值分享组合: 签名的 s 值分享组合: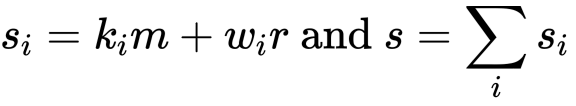 至此,门限 ECDSA 签名的实现原理已经清晰。?零知识证明?我们用到了零知识证明(ZK Proofs)来检测成员里的恶意行为,采取先签后验的方式,即如果最终的签名未验证通过则证明至少一个成员未遵循规则。但是我们需要确保这个过程中(正确执行和中止执行)诚实成员暴露的信息不会被恶意利用。?通信模型?假设存在一个点对点的广播通道(broadcast channel)用于连接每一对成员通信。恶意攻击者至多控制 t 个成员(dishonest majority),且 t <= n-1,我们假设攻击者是最后“说话”的,即看到诚实成员的信息后选择自己的信息方案。目前的协议并不保障 liveness,即可能无法完成协议运行。?加法同态加密?对于给定的两个基于同态加密算法 E 的密文: 至此,门限 ECDSA 签名的实现原理已经清晰。?零知识证明?我们用到了零知识证明(ZK Proofs)来检测成员里的恶意行为,采取先签后验的方式,即如果最终的签名未验证通过则证明至少一个成员未遵循规则。但是我们需要确保这个过程中(正确执行和中止执行)诚实成员暴露的信息不会被恶意利用。?通信模型?假设存在一个点对点的广播通道(broadcast channel)用于连接每一对成员通信。恶意攻击者至多控制 t 个成员(dishonest majority),且 t <= n-1,我们假设攻击者是最后“说话”的,即看到诚实成员的信息后选择自己的信息方案。目前的协议并不保障 liveness,即可能无法完成协议运行。?加法同态加密?对于给定的两个基于同态加密算法 E 的密文: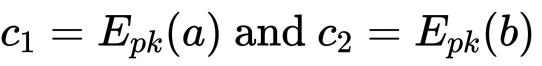 定义同态加操作: 定义同态加操作: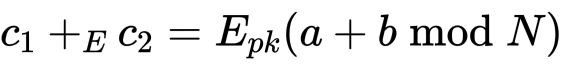 定义标量乘法操作: 定义标量乘法操作: ?不可延展的陷门承诺协议?通常一个(非交互)陷门承诺(trapdoor commitment)机制包含四部分算法:(1)KG:密钥生成算法,输入一个安全参数,输出密钥对 {pk, tk},其中 pk 是与承诺机制有关的公钥,tk 为陷门;(2)Com:承诺算法;(3)Ver:验证算法;(4)Equiv:通过给定的陷门打开承诺算法。?一个陷门承诺需要满足以下属性:(a)Correctness;(b)Information Theoretic Security(信息论安全);(c)Secure Binding。?所谓承诺是不可展的(non-malleable)指,对于给定信息 m 的承诺 C,攻击者在看到承诺打开后,不可能找到另一个承诺 C',使之可以成功解承诺后得到消息 m',否则攻击者可以换成自己的承诺,使真正的承诺无效。?可验证秘密分享协议?即?Feldman's VSS。对于一个可验证秘密分享协议,会有一个辅助信息(auxiliary information)被公开,以便允许成员可以据此验证它们的秘密碎片是否始终如一并可以构建出唯一的秘密。Feldman 方案便是对于 Shamir 秘密分享的一种可验证扩展。??份额变换?是计算秘密值乘法运算的重要 MPC 原语。假定 Alice 和 Bob 分别拥有秘密 a 和 b,对于 ab 的乘法分享,令 x = ab mod q,Alice 和 Bob 需要计算 x 的秘密加法分享 ?不可延展的陷门承诺协议?通常一个(非交互)陷门承诺(trapdoor commitment)机制包含四部分算法:(1)KG:密钥生成算法,输入一个安全参数,输出密钥对 {pk, tk},其中 pk 是与承诺机制有关的公钥,tk 为陷门;(2)Com:承诺算法;(3)Ver:验证算法;(4)Equiv:通过给定的陷门打开承诺算法。?一个陷门承诺需要满足以下属性:(a)Correctness;(b)Information Theoretic Security(信息论安全);(c)Secure Binding。?所谓承诺是不可展的(non-malleable)指,对于给定信息 m 的承诺 C,攻击者在看到承诺打开后,不可能找到另一个承诺 C',使之可以成功解承诺后得到消息 m',否则攻击者可以换成自己的承诺,使真正的承诺无效。?可验证秘密分享协议?即?Feldman's VSS。对于一个可验证秘密分享协议,会有一个辅助信息(auxiliary information)被公开,以便允许成员可以据此验证它们的秘密碎片是否始终如一并可以构建出唯一的秘密。Feldman 方案便是对于 Shamir 秘密分享的一种可验证扩展。??份额变换?是计算秘密值乘法运算的重要 MPC 原语。假定 Alice 和 Bob 分别拥有秘密 a 和 b,对于 ab 的乘法分享,令 x = ab mod q,Alice 和 Bob 需要计算 x 的秘密加法分享 这里我们呈现一个基于加法同态的协议。(1)Alice 初始化协议:向 Bob 发送 这里我们呈现一个基于加法同态的协议。(1)Alice 初始化协议:向 Bob 发送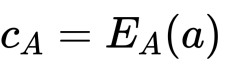 (2)Bob 计算密文 (2)Bob 计算密文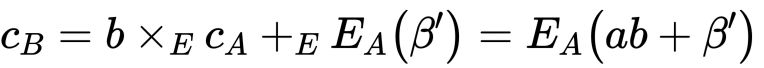 Bob 设置他的分享 Bob 设置他的分享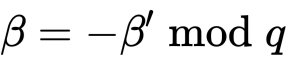 回复 Alice。(3)Alice 解密 cB 得 回复 Alice。(3)Alice 解密 cB 得 ?sMPC 协议?我们假设每个成员 Pi 都拥有加法同态加密机制下的公钥 Ei。(1)密钥生成协议共存在 n 个并发 VSS 协议分发成员各自的秘密值,每个成员收集拼装来自其他 n-1 个成员的秘密值碎片,所以理论上在复现最终总私钥时,需要进行 n 次多方计算。?(2)生成签名(a)Phase 1:每个成员选择各自的秘密值 ?sMPC 协议?我们假设每个成员 Pi 都拥有加法同态加密机制下的公钥 Ei。(1)密钥生成协议共存在 n 个并发 VSS 协议分发成员各自的秘密值,每个成员收集拼装来自其他 n-1 个成员的秘密值碎片,所以理论上在复现最终总私钥时,需要进行 n 次多方计算。?(2)生成签名(a)Phase 1:每个成员选择各自的秘密值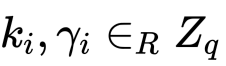 (b)Phase 2:两两一对参与到一个两方“乘转加”(multiplicativ-to-additive)份额变换(share conversion)的子协议中(详见[1]),计算出 —— (b)Phase 2:两两一对参与到一个两方“乘转加”(multiplicativ-to-additive)份额变换(share conversion)的子协议中(详见[1]),计算出 ——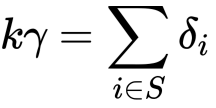 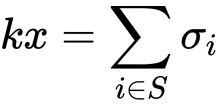 依此进一步得到 r。(c)Phase 3:每个成员 Pi 设置各自的 依此进一步得到 r。(c)Phase 3:每个成员 Pi 设置各自的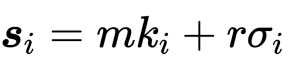 注意到有 注意到有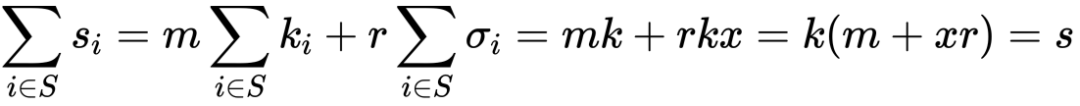 为对 s 的一个 (t, t) 分享,最终得 为对 s 的一个 (t, t) 分享,最终得 ?
引用
?[1] Rosario Gennaro and Steven Goldfeder. “Fast Multiparty Threshold ECDSA with Fast Trustless Setup”. English. In: ACM, 2018, pp. 1179– 1194. isbn: 9781450356930;1450356931;https://eprint.iacr.org/2019/114.pdf?[2] Software for the SPDZ, MASCOT, and Overdrive secure multi-party computation protocols.?https://github.com/bristolcrypto/SPDZ-2 ?
引用
?[1] Rosario Gennaro and Steven Goldfeder. “Fast Multiparty Threshold ECDSA with Fast Trustless Setup”. English. In: ACM, 2018, pp. 1179– 1194. isbn: 9781450356930;1450356931;https://eprint.iacr.org/2019/114.pdf?[2] Software for the SPDZ, MASCOT, and Overdrive secure multi-party computation protocols.?https://github.com/bristolcrypto/SPDZ-2
—-
编译者/作者:比原链
玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。
|




 ?我们把这种全链接式的跨链方式称为交叉跨链。交叉跨链拥有以下四个深远意义:(a)BTC资产可以在多个公链生态体系内无缝切换,随应用而流转,让小生态公链体系可以与大生态公链体系重合,获得更多用户和流量,而大生态公链体系可以捕获更为强悍的二层网络和化身资产;(b)定义可编程跨链时代的来临。交叉跨链也是一个分布式系统,拥有抵押治理和共识容错,它可以灵活解析来自用户发起的任何类型的跨链交易,包括方向、数量、附加数据和更为具体的指令,比如跨链切分、部分延迟、条件式触发等;(c)发展成为一种被广泛接受的统一跨链标准、协议层;(d)发掘最优跨链路径和最优化身资产。
可编程跨链网关?
用户可在交叉跨链系统界面自由定义一组跨链交易的脚本:(1)一笔锁定资产向不同公链铸币,数量、时间、映射地址都可以设定;(2)一笔锁定资产,先定义向公链 A 铸币,再定义将 A 的铸币燃烧,并在公链 B 上铸币;(3)一笔锁定资产,延迟触发。?可以让一笔资产彻底无法追踪,可以实现事件驱动的跨链。?
联邦分布式系统
分布式系统的必要性?跨链网关系统最高效的实现是见证人机制,OFMF 在见证人机制的基础上将网关节点进一步开放出去,以寻求去中心化的权力构成,符合一个公链生态扩大自身规模的愿景。但见证人机制的性能瓶颈受制于两方面,一是所链接的两条公链上原生交易的确认速度,二是见证人系统自身的决策效率。前者没有太大优化空间,后者的瓶颈可以进一步拆分成两种:(i)见证人共同执行跨链签名的效率;(ii)见证人重组的效率。?最理想的跨链网关系统是一个可以主动获取可靠原始验证数据并自主进行分布式决策的自动化网络,并不需要人工去操纵跨链签名的合法性判断和生成,能够引入成熟机密信息管理保管在线秘密和密钥,能够迅速主动捕获两公链上随时发生的跨链事件并建立存储,然后在判断交易合法性的前提下进行安全多方计算快速生成跨链交易签名,依靠分布式容错共识算法自动去除恶意节点的干扰,依托门限签名节省多方签名的费用成本和时间成本,尤其是在网关网络规模不断扩大走向更为开放的进程中,效用更为显著。MOV 交叉跨链系统也是在 OFMF 框架上升级为完全分布式网络系统,更大程度的利用安全多方计算和共识算法决策的性质,来提升整个跨链网关的效率和安全。?由 Fednodes 组成的分布式系统,每周期换届选举出新的决策 Fednodes 节点集合,跟一条链系统有着本质的相似,但没有资产和账户体系,没有转账交易,只对跨链事件进行共识见证,并协作执行门限签名进行铸币、燃烧和释放等操作,能够准确解析用户的每一笔跨链交易请求或者脚本。?由于交叉跨链系统的无准入特性,以及门限签名的合成是一个多方在线交互验证的分布式协作过程,当存在未知数量的恶意节点或者网络出现分区的情况下,可能无法就某一笔跨链交易进行共识验证并生成合法的门限签名,导致网关网络的阻塞或者被攻击,影响跨链系统的效率以及安全性。针对每一笔跨链请求,Fednodes 需要能够就跨链请求序列(包括交叉跨链系统记录的请求序列以及跨链交易在链上被打包区块并确认的序列)、跨链请求的正确性(类似区块链上的转账交易的正确性)达成一致,并且对每一笔合法跨链请求执行(execute)安全多方计算过程,该过程依然是一个依托共识网络完成门限签名的过程,确保在有限时间内完成合法门限签名的签署和执行。?sMPC 过程涉及多次(并发/多轮)随机秘密份额的分布式生成与交互验证(DKG/VSS/RNG/arithmetic operation/inverse/multiplicativ-to-additive),是实现多方安全计算的核心,并且处于异步网络通信环境里,延迟不可预测,另外恶意节点会对节点间份额集合的一致性进行干扰攻击,例如恶意节点给一部分诚实节点一种秘密份额子集,但是给另一部分诚实节点另外一种子集,在缺乏多轮交互确认以及可靠广播信道的系统里这种行为极具破坏性。因此 Fednodes 的分布式网络应该是一种拜占庭容错的一致性系统,即便阈值范围内的节点出现 slow/fault/failure/crash 或者 Byzantine 行为,也不妨碍系统继续完成协作,否则整个系统的效率将极大被阻塞影响。这种拜占庭容错系统可以更细分为 replicated state machines 和 Byzantine quorum systems 两种。后者一般适用于只涉及读和写等简单的语义,基于前者 MOV 交叉跨链系统将实现一种契合安全多方计算过程的 Asynchronous Byzantine Broadcast Protocols,用于消息(见证跨链事件/安全多方计算门限签名)的防拜占庭可靠传输,并灵活适配于各种网络模型(同步网络/半同步网络)。??Reliable Broadcast?我们构建?Reliable broadcast(RBC),一种针对拜占庭将军问题的广播模型,满足下面特性:?
Validity:如果一个诚实节点广播(r-broadcast)一条消息 <ID.j.s, m>,那么所有的诚实节点都将收到(r-deliver)同样的消息。Consistency:如果一些诚实节点 r-deliver 了消息 <ID.j.s, m>,另一些诚实节点 r-deliver 了消息 <ID.j.s, m′>,那么 m = m′。Totality:如果一些诚实节点 r-deliver 了序号为 ID.j.s 的消息,那么所有的诚实节点都将 r-deliver 同样序号的消息。Integrity:每个诚实节点只能 r-deliver 最多一条 ID.j.s 标识下的消息 m。Efficiency:每个 D.j.s 序号下的 broadcast 实例的通信复杂度都是 uniformly bounded。
Validity 保证了算法的 liveness,Consistency 和 Totality 是对传统定义 agreement 的拆分,拆分的缘由之一是不保证 totality 的 reliable broadcast 也是一 种有用的方法。?基于此我们构建协议如下 ——(1)当收到消息 (ID.j.s, in, r-broadcast, m),执行:
?我们把这种全链接式的跨链方式称为交叉跨链。交叉跨链拥有以下四个深远意义:(a)BTC资产可以在多个公链生态体系内无缝切换,随应用而流转,让小生态公链体系可以与大生态公链体系重合,获得更多用户和流量,而大生态公链体系可以捕获更为强悍的二层网络和化身资产;(b)定义可编程跨链时代的来临。交叉跨链也是一个分布式系统,拥有抵押治理和共识容错,它可以灵活解析来自用户发起的任何类型的跨链交易,包括方向、数量、附加数据和更为具体的指令,比如跨链切分、部分延迟、条件式触发等;(c)发展成为一种被广泛接受的统一跨链标准、协议层;(d)发掘最优跨链路径和最优化身资产。
可编程跨链网关?
用户可在交叉跨链系统界面自由定义一组跨链交易的脚本:(1)一笔锁定资产向不同公链铸币,数量、时间、映射地址都可以设定;(2)一笔锁定资产,先定义向公链 A 铸币,再定义将 A 的铸币燃烧,并在公链 B 上铸币;(3)一笔锁定资产,延迟触发。?可以让一笔资产彻底无法追踪,可以实现事件驱动的跨链。?
联邦分布式系统
分布式系统的必要性?跨链网关系统最高效的实现是见证人机制,OFMF 在见证人机制的基础上将网关节点进一步开放出去,以寻求去中心化的权力构成,符合一个公链生态扩大自身规模的愿景。但见证人机制的性能瓶颈受制于两方面,一是所链接的两条公链上原生交易的确认速度,二是见证人系统自身的决策效率。前者没有太大优化空间,后者的瓶颈可以进一步拆分成两种:(i)见证人共同执行跨链签名的效率;(ii)见证人重组的效率。?最理想的跨链网关系统是一个可以主动获取可靠原始验证数据并自主进行分布式决策的自动化网络,并不需要人工去操纵跨链签名的合法性判断和生成,能够引入成熟机密信息管理保管在线秘密和密钥,能够迅速主动捕获两公链上随时发生的跨链事件并建立存储,然后在判断交易合法性的前提下进行安全多方计算快速生成跨链交易签名,依靠分布式容错共识算法自动去除恶意节点的干扰,依托门限签名节省多方签名的费用成本和时间成本,尤其是在网关网络规模不断扩大走向更为开放的进程中,效用更为显著。MOV 交叉跨链系统也是在 OFMF 框架上升级为完全分布式网络系统,更大程度的利用安全多方计算和共识算法决策的性质,来提升整个跨链网关的效率和安全。?由 Fednodes 组成的分布式系统,每周期换届选举出新的决策 Fednodes 节点集合,跟一条链系统有着本质的相似,但没有资产和账户体系,没有转账交易,只对跨链事件进行共识见证,并协作执行门限签名进行铸币、燃烧和释放等操作,能够准确解析用户的每一笔跨链交易请求或者脚本。?由于交叉跨链系统的无准入特性,以及门限签名的合成是一个多方在线交互验证的分布式协作过程,当存在未知数量的恶意节点或者网络出现分区的情况下,可能无法就某一笔跨链交易进行共识验证并生成合法的门限签名,导致网关网络的阻塞或者被攻击,影响跨链系统的效率以及安全性。针对每一笔跨链请求,Fednodes 需要能够就跨链请求序列(包括交叉跨链系统记录的请求序列以及跨链交易在链上被打包区块并确认的序列)、跨链请求的正确性(类似区块链上的转账交易的正确性)达成一致,并且对每一笔合法跨链请求执行(execute)安全多方计算过程,该过程依然是一个依托共识网络完成门限签名的过程,确保在有限时间内完成合法门限签名的签署和执行。?sMPC 过程涉及多次(并发/多轮)随机秘密份额的分布式生成与交互验证(DKG/VSS/RNG/arithmetic operation/inverse/multiplicativ-to-additive),是实现多方安全计算的核心,并且处于异步网络通信环境里,延迟不可预测,另外恶意节点会对节点间份额集合的一致性进行干扰攻击,例如恶意节点给一部分诚实节点一种秘密份额子集,但是给另一部分诚实节点另外一种子集,在缺乏多轮交互确认以及可靠广播信道的系统里这种行为极具破坏性。因此 Fednodes 的分布式网络应该是一种拜占庭容错的一致性系统,即便阈值范围内的节点出现 slow/fault/failure/crash 或者 Byzantine 行为,也不妨碍系统继续完成协作,否则整个系统的效率将极大被阻塞影响。这种拜占庭容错系统可以更细分为 replicated state machines 和 Byzantine quorum systems 两种。后者一般适用于只涉及读和写等简单的语义,基于前者 MOV 交叉跨链系统将实现一种契合安全多方计算过程的 Asynchronous Byzantine Broadcast Protocols,用于消息(见证跨链事件/安全多方计算门限签名)的防拜占庭可靠传输,并灵活适配于各种网络模型(同步网络/半同步网络)。??Reliable Broadcast?我们构建?Reliable broadcast(RBC),一种针对拜占庭将军问题的广播模型,满足下面特性:?
Validity:如果一个诚实节点广播(r-broadcast)一条消息 <ID.j.s, m>,那么所有的诚实节点都将收到(r-deliver)同样的消息。Consistency:如果一些诚实节点 r-deliver 了消息 <ID.j.s, m>,另一些诚实节点 r-deliver 了消息 <ID.j.s, m′>,那么 m = m′。Totality:如果一些诚实节点 r-deliver 了序号为 ID.j.s 的消息,那么所有的诚实节点都将 r-deliver 同样序号的消息。Integrity:每个诚实节点只能 r-deliver 最多一条 ID.j.s 标识下的消息 m。Efficiency:每个 D.j.s 序号下的 broadcast 实例的通信复杂度都是 uniformly bounded。
Validity 保证了算法的 liveness,Consistency 和 Totality 是对传统定义 agreement 的拆分,拆分的缘由之一是不保证 totality 的 reliable broadcast 也是一 种有用的方法。?基于此我们构建协议如下 ——(1)当收到消息 (ID.j.s, in, r-broadcast, m),执行: (广播/r-send)?(2)当节点收到来自 Leader 节点 Pι 的消息 (ID.j.s, r-send, m),执行:
(广播/r-send)?(2)当节点收到来自 Leader 节点 Pι 的消息 (ID.j.s, r-send, m),执行: (广播/r-echo/第一阶段)?(3)当节点收到来自其他节点的消息 (ID.j.s, r-echo, d):
(广播/r-echo/第一阶段)?(3)当节点收到来自其他节点的消息 (ID.j.s, r-echo, d): (满足阈值后广播/r-ready/第二阶段)?(4)当节点收到来自其他节点的消息 (ID.j.s, r-ready, d):
(满足阈值后广播/r-ready/第二阶段)?(4)当节点收到来自其他节点的消息 (ID.j.s, r-ready, d): (满足拜占庭容错阈值后输出/r-deliver/第三阶段)?(*)在收到消息 (ID.j.s, r-request) 后执行:
(满足拜占庭容错阈值后输出/r-deliver/第三阶段)?(*)在收到消息 (ID.j.s, r-request) 后执行: (获取最新消息内容/r-answer)??
(获取最新消息内容/r-answer)?? ??RBC 传承了经典拜占庭容错共识的三阶段,同时引入了更为可靠的消息传输,十分适合安全多方计算网络的秘密份额传输和合成。Reliable broadcast 分为 “echo” 和 “ready” 两个关键阶段,echo 阶段保证每个节点都 accept 到了同样的消息(consistency),ready 阶段保证如果一个人 accept 了一条消息 M,那么其他所有节点也都 accept 了 M(reliability)。?整体上消息复杂度是 O(N^2)。如果没有 fault 出现,复杂度可降为:
??RBC 传承了经典拜占庭容错共识的三阶段,同时引入了更为可靠的消息传输,十分适合安全多方计算网络的秘密份额传输和合成。Reliable broadcast 分为 “echo” 和 “ready” 两个关键阶段,echo 阶段保证每个节点都 accept 到了同样的消息(consistency),ready 阶段保证如果一个人 accept 了一条消息 M,那么其他所有节点也都 accept 了 M(reliability)。?整体上消息复杂度是 O(N^2)。如果没有 fault 出现,复杂度可降为: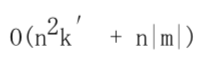 注:m 是发送的消息,k′ 是 hash 的长度。但是需要注意的是恶意攻击者会阻塞 r-send 过程导致开销增大。?
安全多方计算
门限 ECDSA 签名?近些年来人们在不断追寻更为通用和灵活的 (t, n) 门限方案,即 n >= t+1,且只需要 t+1 方即可完成签名。但是更多的阻碍出现在了分布式密钥生成协议(DKG)上,往往都是极具消耗性的,难以用于实际生产。?在通用的 DSA 签名算法中,假设循环群 G 由素数阶 q 和基点 g 来定义,密钥(secret key) x 统一从以素数 q 为模数的有限域 Z/q 中随机选取,从 Z/q 中随机选取 k。对 DSA 门限签名的实现难度在于需要多方共同来计算 R(涉及 g 求幂和 k 求反操作)和 s(涉及两个秘密值 k 和 x 的乘操作),这种非线性的计算对多方安全计算来说是十分困难的。[1] 受到著名的 MPC 实现 SPDZ [2] 的启发,采用了一种不同的多方计算法:假设有两个秘密值 a 和 b 在多方之间分享,有 a = a1+...+an,b = b1+...+bn,对于参与方 Pi 拥有 ai 和 bi;此时我们需要生成 c = ab 的分享,注意到有
注:m 是发送的消息,k′ 是 hash 的长度。但是需要注意的是恶意攻击者会阻塞 r-send 过程导致开销增大。?
安全多方计算
门限 ECDSA 签名?近些年来人们在不断追寻更为通用和灵活的 (t, n) 门限方案,即 n >= t+1,且只需要 t+1 方即可完成签名。但是更多的阻碍出现在了分布式密钥生成协议(DKG)上,往往都是极具消耗性的,难以用于实际生产。?在通用的 DSA 签名算法中,假设循环群 G 由素数阶 q 和基点 g 来定义,密钥(secret key) x 统一从以素数 q 为模数的有限域 Z/q 中随机选取,从 Z/q 中随机选取 k。对 DSA 门限签名的实现难度在于需要多方共同来计算 R(涉及 g 求幂和 k 求反操作)和 s(涉及两个秘密值 k 和 x 的乘操作),这种非线性的计算对多方安全计算来说是十分困难的。[1] 受到著名的 MPC 实现 SPDZ [2] 的启发,采用了一种不同的多方计算法:假设有两个秘密值 a 和 b 在多方之间分享,有 a = a1+...+an,b = b1+...+bn,对于参与方 Pi 拥有 ai 和 bi;此时我们需要生成 c = ab 的分享,注意到有 需要对每一项秘密值 aibj 都进行分享;这给予的启示是,可以让参与方们根据各自拥有的 a 和 b 的秘密份额两两配对组合生成秘密值 aibj,基于此创建一种简单而又优雅的门限 ECDSA 协议。根据上面提到的原理计算乘法分享:?
需要对每一项秘密值 aibj 都进行分享;这给予的启示是,可以让参与方们根据各自拥有的 a 和 b 的秘密份额两两配对组合生成秘密值 aibj,基于此创建一种简单而又优雅的门限 ECDSA 协议。根据上面提到的原理计算乘法分享:?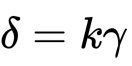
 因此可以获得 R 的多方计算:
因此可以获得 R 的多方计算: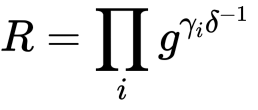 签名的 s 值分享组合:
签名的 s 值分享组合: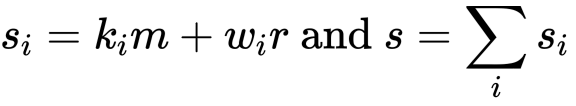 至此,门限 ECDSA 签名的实现原理已经清晰。?零
至此,门限 ECDSA 签名的实现原理已经清晰。?零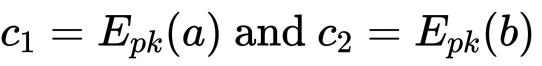 定义同态加操作:
定义同态加操作: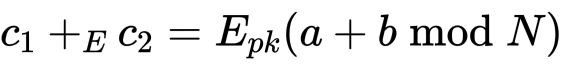 定义标量乘法操作:
定义标量乘法操作: ?不可延展的陷门承诺协议?通常一个(非交互)陷门承诺(trapdoor commitment)机制包含四部分算法:(1)KG:密钥生成算法,输入一个安全参数,输出密钥对 {pk, tk},其中 pk 是与承诺机制有关的公钥,tk 为陷门;(2)Com:承诺算法;(3)Ver:验证算法;(4)Equiv:通过给定的陷门打开承诺算法。?一个陷门承诺需要满足以下属性:(a)Correctness;(b)Information Theoretic Security(信息论安全);(c)Secure Binding。?所谓承诺是不可展的(non-malleable)指,对于给定信息 m 的承诺 C,攻击者在看到承诺打开后,不可能找到另一个承诺 C',使之可以成功解承诺后得到消息 m',否则攻击者可以换成自己的承诺,使真正的承诺无效。?可验证秘密分享协议?即?Feldman's VSS。对于一个可验证秘密分享协议,会有一个辅助信息(auxiliary information)被公开,以便允许成员可以据此验证它们的秘密碎片是否始终如一并可以构建出唯一的秘密。Feldman 方案便是对于 Shamir 秘密分享的一种可验证扩展。??份额变换?是计算秘密值乘法运算的重要 MPC 原语。假定 Alice 和 Bob 分别拥有秘密 a 和 b,对于 ab 的乘法分享,令 x = ab mod q,Alice 和 Bob 需要计算 x 的秘密加法分享
?不可延展的陷门承诺协议?通常一个(非交互)陷门承诺(trapdoor commitment)机制包含四部分算法:(1)KG:密钥生成算法,输入一个安全参数,输出密钥对 {pk, tk},其中 pk 是与承诺机制有关的公钥,tk 为陷门;(2)Com:承诺算法;(3)Ver:验证算法;(4)Equiv:通过给定的陷门打开承诺算法。?一个陷门承诺需要满足以下属性:(a)Correctness;(b)Information Theoretic Security(信息论安全);(c)Secure Binding。?所谓承诺是不可展的(non-malleable)指,对于给定信息 m 的承诺 C,攻击者在看到承诺打开后,不可能找到另一个承诺 C',使之可以成功解承诺后得到消息 m',否则攻击者可以换成自己的承诺,使真正的承诺无效。?可验证秘密分享协议?即?Feldman's VSS。对于一个可验证秘密分享协议,会有一个辅助信息(auxiliary information)被公开,以便允许成员可以据此验证它们的秘密碎片是否始终如一并可以构建出唯一的秘密。Feldman 方案便是对于 Shamir 秘密分享的一种可验证扩展。??份额变换?是计算秘密值乘法运算的重要 MPC 原语。假定 Alice 和 Bob 分别拥有秘密 a 和 b,对于 ab 的乘法分享,令 x = ab mod q,Alice 和 Bob 需要计算 x 的秘密加法分享 这里我们呈现一个基于加法同态的协议。(1)Alice 初始化协议:向 Bob 发送
这里我们呈现一个基于加法同态的协议。(1)Alice 初始化协议:向 Bob 发送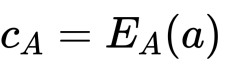 (2)Bob 计算密文
(2)Bob 计算密文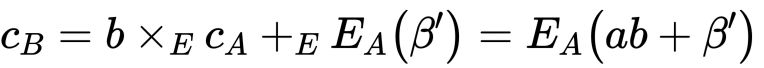 Bob 设置他的分享
Bob 设置他的分享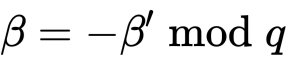 回复 Alice。(3)Alice 解密 cB 得
回复 Alice。(3)Alice 解密 cB 得 ?sMPC 协议?我们假设每个成员 Pi 都拥有加法同态加密机制下的公钥 Ei。(1)密钥生成协议共存在 n 个并发 VSS 协议分发成员各自的秘密值,每个成员收集拼装来自其他 n-1 个成员的秘密值碎片,所以理论上在复现最终总私钥时,需要进行 n 次多方计算。?(2)生成签名(a)Phase 1:每个成员选择各自的秘密值
?sMPC 协议?我们假设每个成员 Pi 都拥有加法同态加密机制下的公钥 Ei。(1)密钥生成协议共存在 n 个并发 VSS 协议分发成员各自的秘密值,每个成员收集拼装来自其他 n-1 个成员的秘密值碎片,所以理论上在复现最终总私钥时,需要进行 n 次多方计算。?(2)生成签名(a)Phase 1:每个成员选择各自的秘密值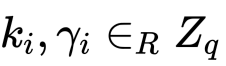 (b)Phase 2:两两一对参与到一个两方“乘转加”(multiplicativ-to-additive)份额变换(share conversion)的子协议中(详见[1]),计算出 ——
(b)Phase 2:两两一对参与到一个两方“乘转加”(multiplicativ-to-additive)份额变换(share conversion)的子协议中(详见[1]),计算出 ——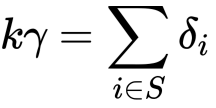
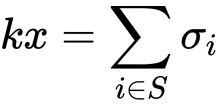 依此进一步得到 r。(c)Phase 3:每个成员 Pi 设置各自的
依此进一步得到 r。(c)Phase 3:每个成员 Pi 设置各自的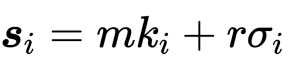 注意到有
注意到有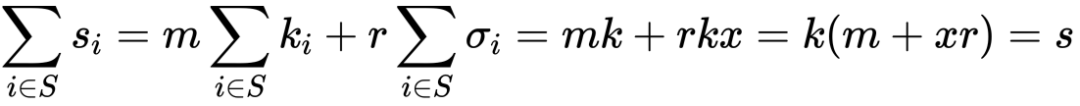 为对 s 的一个 (t, t) 分享,最终得
为对 s 的一个 (t, t) 分享,最终得 ?
引用
?[1] Rosario Gennaro and Steven Goldfeder. “Fast Multiparty Threshold ECDSA with Fast Trustless Setup”. English. In: ACM, 2018, pp. 1179– 1194. isbn: 9781450356930;1450356931;https://eprint.iacr.org/2019/114.pdf?[2] Software for the SPDZ, MASCOT, and Overdrive secure multi-party computation protocols.?https://github.com/bristolcrypto/SPDZ-2
?
引用
?[1] Rosario Gennaro and Steven Goldfeder. “Fast Multiparty Threshold ECDSA with Fast Trustless Setup”. English. In: ACM, 2018, pp. 1179– 1194. isbn: 9781450356930;1450356931;https://eprint.iacr.org/2019/114.pdf?[2] Software for the SPDZ, MASCOT, and Overdrive secure multi-party computation protocols.?https://github.com/bristolcrypto/SPDZ-2
