链上账本数据写入慢？试试LSM

导 ?读

首先问大家一个小问题？区块链的账本数据存储格式主要是什么类型的？

相信聪明的你一定知道是Key-Value类型存储。

下一个问题，这些Key-Value数据在底层数据库如何高效组织？

答案就是我们本期介绍的内容：LSM[1]。

LSM是一种被广泛采用的持久化Key-Value存储方案，如LevelDB, RocksDB, Cassandra等数据库均采用LSM作为其底层存储引擎。

据公开数据调研，LSM是当前市面上写密集应用的最佳解决方案，也是区块链领域被应用最多的一种存储模式，今天我们将对LSM基本概念和性能进行介绍和分析。

LSM-Tree背景：追本溯源

LSM-Tree的设计思想来自于一个计算机领域一个老生常谈的话题——对存储介质的顺序操作效率远高于随机操作。

如图1所示，对磁盘的顺序操作甚至可以快过对内存的随机操作，而对同一类磁盘，其顺序操作的速度比随机操作高出三个数量级以上[2]，因此我们可以得出一个非常直观的结论：应当充分利用顺序读写而尽可能避免随机读写。

Figure?1?Random access vs. Sequential access

考虑到这一点，如果我们想尽可能提高写操作的吞吐量，那么最好的方法一定是不断地将数据追加到文件末尾，该方法可将写入吞吐量提高至磁盘的理论水平，然而也有显而易见的弊端，即读效率极低（这也是许多数据库避免数据意外丢失的手段，因通常不需要对其进行读取，称为Journaling或WAL），我们称这种数据更新是非原地的（Out-of-place），与之相对的是原地更新（In-place）。

为了提高读取效率，一种常用的方法是增加索引信息，如B+树, ISAM等，对这类数据结构进行数据（或索引）的更新是原地进行的，这将不可避免地引入随机IO。

LSM-Tree与传统多叉树的数据组织形式完全不同，可以认为LSM-Tree是完全以磁盘为中心（Disk-Centric）的一种数据结构，其只需要少量的内存来提升效率，而可以尽可能地通过上文提到的Journaling方式来提高写入吞吐量。当然，其读取效率会稍逊于B+树。

LSM-Tree数据结构：抽丝剥茧

图2展示了LSM-Tree的理论模型(a)和一种实现方式(b)[3]。LSM-Tree是一种层级的数据结构，包含一层空间占用较小的内存结构以及多层磁盘结构，每一层磁盘结构的空间上限呈指数增长，如在LevelDB中该系数默认为10。

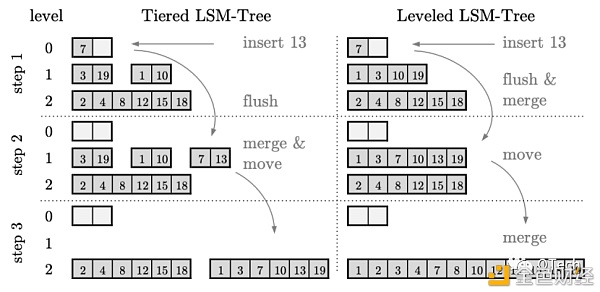
Figure?2?LSM与其LevelDB实现

对于LSM-Tree的数据插入或更新，首先会被缓存在内存中，这部分数据往往由一颗排序树进行组织。

当缓存达到预设上限，则会将内存中的数据以有序的方式写入磁盘（即L0层），我们称这样的有序列为一个Sorted Run，简称为Run。

随着写入操作的不断进行，L0层会堆积越来越多的Run，且显然不同的Run之前可能存在重叠部分（如Run-1的数据范围是a-c，Run-2的数据范围是b-d），此时进行某一条数据的查询将无法准确判断该数据存在于哪个Run中，因此最坏情况下需要进行等同于L0层Run数量的I/O。

为了解决该问题，当某一层的Run数目或大小到达某一阈值后，LSM-Tree会进行后台的归并排序，并将排序结果输出至下一层，我们将一次归并排序称为Compaction。如同B+树的分裂一样，Compaction是LSM-Tree维持相对稳定读写效率的核心机制，我们将会在下文详细介绍两种不同的Compaction策略。

另外值得一提的是，无论是从内存到磁盘的写入，还是磁盘中不断进行的Compaction，都是对磁盘的顺序I/O，这就是LSM拥有更高写入吞吐量的原因。

Leveling vs. Tiering：一读一写，不分伯仲

LSM-Tree的Compaction策略可以分为Leveling和Tiering两种，前者被LevelDB，RocksDB等采用，后者被Cassandra等采用，称采用Leveling策略的的LSM-Tree为Leveled?LSM-Tree，采用Tiering的LSM-Tree为Tiered?LSM-Tree，如图3所示[4]。

Figure?3?两种Compaction策略对比

▲Leveling

简而言之，Tiering是写友好型的策略，而Leveling是读友好型的策略。在Leveling中，除了L0的每一层最多只能有一个Run（Run为一组有序且不重叠的序列，可以考虑LevelDB中除了L0每一层中的SSTable都是有序且互相不重叠的，统称这些SSTable为一个Run），如图3右侧所示，当在L0插入13时，触发了L0层的Compaction，此时会对Run-L0与下层Run-L1进行一次归并排序，归并结果写入L1，此时又触发了L1的Compaction，此时会对Run-L1与下层Run-L2进行归并排序，归并结果写入L2。

▲Tiering

反观Tiering在进行Compaction时并不会主动与下层的Run进行归并，而只会对发生Compaction的那一层的若干个Run进行归并排序，这也是Tiering的一层会存在多个Run的原因。

▲对比分析

相比而言，Leveling方式进行得更加贪婪，进行了更多的磁盘I/O，维持了更高的读效率（每一层只有一个Run），而Tiering则相正好反。

本节我们将对LSM-Tree的设计空间进行更加形式化的分析。

LSM层数

布隆过滤器

LSM-Tree应用布隆过滤器来加速查找，LSM-Tree为每个Run设置一个布隆过滤器，在通过I/O查询某个Run之前，首先通过布隆过滤器判断待查询的数据是否存在于该Run，若布隆过滤器返回Negative，则可断言不存在，直接跳到下个Run进行查询，从而节省了一次I/O；而若布隆过滤器返回Positive，则仍不能确定数据是否存在，需要消耗一次I/O去查询该Run，若成功查询到数据，则终止查找，否则继续查找下一个Run，我们称后者为假阳（False Positive）现象，布隆过滤器的过高的假阳率（False Positive Rate, FPR）会严重影响读性能，使得花费在布隆过滤器上的内存形同虚设。限于篇幅本文不对布隆过滤器做更多的介绍，直接给出FPR的计算公式，为公式2.

其中是为布隆过滤器设置的内存大小，为每个Run中的数据总数。

读写I/O

考虑读写操作的最坏场景，对于读操作，认为其最坏场景是空读，即遍历每一层的每个Run，最后发现所读数据并不存在；对于写操作，认为其最坏场景是一条数据的写入会导致每一层发生一次Compaction。

核心理念：基于场景化的设计空间

基于以上分析，我们可以得出如图4所示的LSM-Tree可基于场景化的设计空间。

简而言之，LSM-Tree的设计空间是：在极端优化写的日志方式（即Journaling方式）与极端优化读的有序列表方式之间的折中，折中策略取决于场景（侧重写还是侧重读），折中方式可以对以下参数进行调整：

当Level间放大比例时，两种Compaction策略的读写开销是一致的，而随着T的不断增加，Leveling和Tiering方式的读开销分别提高/减少。

当T达到上限时，前者只有一层，且一层中只有一个Run，因此其读开销到达最低，即最坏情况下只需要一次I/O，而每次写入都会触发整层的Compaction；

而对于后者当T到达上限时，也只有一层，但是一层中存在：

因此读开销达到最高，而写操作不会触发任何的Compaction，因此写开销达到最低。

Figure?4??LSM由日志到有序列的设计空间

事实上，基于图4及上文的分析可以进行对LSM-Tree的性能进一步的优化，如文献[4]对每一层的布隆过滤器大小进行动态调整，以充分优化内存分配并降低FPR来提高读取效率；文献[5]提出“Lazy Leveling”方式来自适应的选择Compaction策略等。

限于篇幅本文不再对这些优化思路进行介绍，感兴趣的读者可以自行查阅文献。

小结

LSM-Tree提供了相当高的写性能、空间利用率以及非常灵活的配置项可供调优，其仍然是适合区块链应用的最佳存储引擎之一。

本文对LSM-Tree从设计思想、数据结构、两种Compaction策略几个角度进行了由浅入深地介绍，限于篇幅，基于本文之上的对LSM-Tree的调优方法将会在后续文章中介绍。

作者简介

叶晨宇

来自趣链科技基础平台部，区块链账本存储研究小组

参考文献

[1].?O’Neil P, Cheng E, Gawlick D, et al. The log-structured merge-tree (LSM-tree)[J]. Acta Informatica, 1996, 33(4): 351-385.

[2].?Jacobs A. The pathologies of big data[J]. Communications of the ACM, 2009, 52(8): 36-44.

[3].?Lu L, Pillai T S, Gopalakrishnan H, et al. Wisckey: Separating keys from values in ssd-conscious storage[J]. ACM Transactions on Storage (TOS), 2017, 13(1): 1-28.

[4].?Dayan N, Athanassoulis M, Idreos S. Monkey: Optimal navigable key-value store[C]//Proceedings of the 2017 ACM International Conference on Management of Data. 2017: 79-94.

[5].?Dayan N, Idreos S. Dostoevsky: Better space-time trade-offs for LSM-tree based key-value stores via adaptive removal of superfluous merging[C]//Proceedings of the 2018 International Conference on Management of Data. 2018: 505-520.

[6].?Luo C, Carey M J. LSM-based storage techniques: a survey[J]. The VLDB Journal, 2020, 29(1): 393-418.

—-

编译者/作者：趣链科技

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。