作者
缘起
摘要
正文 在NIST专家Mr. Onion爆料BTC防破解思路这篇文章中,我们意识到:黑客破解BTC这件事,就在最近一两年内大概率会发生,区块链将进入"后量子破解时代"。那么币民怎么办,难道等着BTC归零?
算法一直是区块链技术的底层核心。目前的绝大部分算法,都无法抵挡量子攻击。这意味着用户的所有信息,都将暴露在量子计算机面前,包括私钥、钱包、通证;黑客可以任意进出、转移、操纵。量子攻击对数字货币及行业的打击是毁灭性的。而防量子破解算法意味着全行业安全和用户安全。 因此,今天我们要隆重为币圈介绍防量子破解技术及其公链。 防量子破解的基础原理 加密和解密的关键在于算法和数据长度。数据长度越长,解密成本越高;在数据长度相同的情况下,只有靠算法提高解密效率。而所有解密都必须具备经济性,也就是说只有在合理的时间内解密出来才有经济价值。 传统计算机为何破解不了BTC签名? 根源在签名长度。就长度而言,BTC私钥为32个字节,组合数量为$$2^{256}$$(2的256次方)。宇宙原子数是$$10^{82}$$(10的82次方),相当于$$2^{280}$$(2的280次方),也就是10万个千万亿。换句话说BTC私钥的理论数量接近于宇宙所有原子的数量。从这么庞大的样本中找到私钥,几乎是不可能的,也是不经济的。当长度足够不被破解的情况下,算法是没有太大动力去进化的。 量子计算机为何能碾压传统计算机且破解BTC? 根源在于量子计算机的1个比特可以表达多重状态且可并行计算,而传统计算机的1个比特只能表达0或1两种状态且只能串行计算。以谷歌72比特的量子计算机为例,可以表达$$2^{72}$$种状态。当量子比特超过280位,就能表达宇宙原子数量那么多的状态;当量子比特达到300的时候,就能破解一切现有加密算法。 从72比特到300比特,也许大概率就在最近两三年,我们准备好了吗? 防量子破解的终极方法
增加签名长度:但是签名长度越长,增加了恶意人员的解密成本,也增加了非恶意人员的正常加密和解密成本。 发明有效算法:通过高效率算法极大提高加密性能和有密钥方的解密性能,如此就能既防止量子破解又不过分增加签名长度。基于量子计算机不擅长计算的那些问题构造密码,就可以抵抗量子计算的攻击。 敏捷化全体系(对抗):当 SHA-1 不再安全的时候,我们就必须将公钥基础设施 (PKI) 迁移到 SHA-2。通过敏捷柔性的公钥基础设施 (PKI) ,随时与时俱进,替换升级有风险的密码和算法。用一个完整体系对抗单点量子攻击。 BTC市值有多大,防量子破解价值就有多大 多名币圈专家认为:BTC市值有多大,破解BTC的价值就有多大;而防止破解的价值远大于破解BTC的价值。核心原因如下:
量子危机吸引全网关注 量子危机吸引全网关注:量子算力对BTC等数字货币构成毁灭性打击的可能性,吸引了全球币民关注,同时也吸引了整个互联网网民关注。 化危机为防破解大品牌:一旦BTC或者某个币,能抗住现在甚至防住未来的量子算力的破解,那么,全球币民甚至几十亿网民都会意识到数学的威力足以赋予一个数字货币足够的安全性,意识到赋予BTC内在价值的挖矿行为也是足够安全、足够有收益的,那么这个数字货币必将获得全球海量关注和参与,必将拥有现在的主流市值和未来的无限空间。 在"后量子破解时代",防破解公链的价值甚至远大于BTC 因此,谁能在对抗现有且防止未来的量子破解的战争中赢得胜利,谁就能在"后量子破解时代",占据C位,获得全球关注,赢得全球网民认可。 因此,谁能率先在公链中提供防量子加密系统,且能在全球悬赏中抗住各种量子破解的攻击,那么这条链不但会超越BTC公链,还会一统天下,将无法抵御量子攻击的BTC、以太坊等等主流公链远远甩在身后。 NIST发起全球防量子加密算法竞投:第三轮已结束 近年来,在构建量子计算机方面取得了稳步进展。随着量子算力和算法的提升,将越来越严重威胁公钥密码系统,尤其是BTC等基于椭圆曲线密码学的密钥建立方案和数字签名将受到最严重的影响,而散列函数等只会受到轻微影响。 如何征集新的公钥密码算法,以安全对抗拥有量子计算机的对手,且能够无需对现有通信网络协议进行重大变更的情况下进行部署?
美国国家标准与技术研究所(NIST)正通过一个公开竞争过程来选择公钥密码算法。新的公钥密码学标准将为数字签名、公钥加密和密钥建立指定一个或多个附加算法。新的标准将增强联邦信息处理标准(FIPS)186-4,数字签名标准(DSS)[1],以及特别出版物(SP)800-56A修订版3,使用离散对数密码学的成对密钥建立方案建议[2],和SP 800-56B修订版2,使用整数因数密码学的成对密钥建立建议[3]。期望这些算法在可预见的未来,包括在量子计算机破解出现之后,能够很好地保护美国政府的敏感信息。这个竞争过程被称为后量子密码学时代的(PQC时代,Post-Quantum Cryptography)NIST发起的PQC标准化过程。 NIST PQC标准化进程始于2016年12月(https://csrc.nist.gov/projects/post-quantum-cryptography),第一轮征集共有82个候选者提交。 NIST计划在2021年春季或夏季举办第三届NIST PQC标准化会议,希望在只有7个最终候选者和8个备选候选者的情况下。 NIST对PQC标准化工作进展感到高兴,但也认识到当前和未来的研究可能产生一些有前途的方案,而这些方案并不是NIST PQC标准化项目的一部分。
Hero@ACT(Anti cracking Token)防量子破解公链值得关注 小编对几条公链做了深度跟踪和调研,单就防量子破解而言,最近横空出世的Hero@ACT公链,非常值得关注。 小编的推荐理由如下: 技术牛
绿色且节能:共识算法能耗极低 后量子安全:传统安全性等同BTC,在防量子破解上安全性超过BTC 顾问超级牛:团队有NIST第三轮入选算法的核心成员+Erlang OTP框架核心人员 市场猛
九大社区:支持强力 头矿:深受团队长欢迎 Hero游戏:容易裂变 社区强 团队布道:项目方多次提到:团队只是布道者,共同发起防量子公链而已 社区自治:项目方计划:在6个月左右,团队在公链顺利上线后,将还权于社区,公链为社区共有共治共享 文末"参考资料"里面有项目方提供的长图,里面有项目方工作微信号码,有兴趣的可自行加微信 密码和解密的故事 最早用于战争的凯撒密码
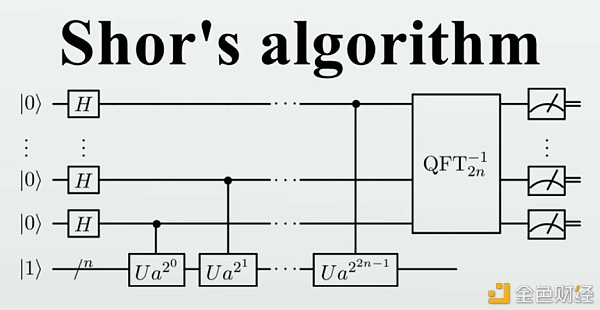
信息的加密和解密(破解),历史源远流长,最早可追溯到古埃及墓墙中的非标象形文字,还有阿拉伯数学家Al-Kindi于1200年前开发的替代密码。而战争中的应用,最早可追溯到公元前罗马共和时期。当年恺撒曾用恺撒密码(Caesar Cipher)与将军们联系。 它是一种替换加密方法,明文中所有字母都在字母表上向后(或向前)偏移固定偏移量后被替换成密文。例如:当偏移量为3,所有字母A将被替换成D,B替换成E,以此类推。 显然!现代世界任何一个程序员,都能借助任何计算机的算力,轻易破解凯撒密码,截获罗马帝国的军事机密。 秀尔算法和RSA算法的矛盾不可调和 今天的通讯安全、BTC的密码安全,都源于一站二战以来,所有科学家在过去100年的努力。某种意义上,这是来自过去的技术;而量子计算机横空出世,极大的减弱了传统加密方式的防御能力。 量子计算机基于秀尔算法(Shor’s algorithm),在打破基于Rivest–Shamir–Adleman(RSA)和椭圆曲线加密(ECC)的加密,可能比传统计算机更有效。这两种是当前最常见的加密类型。
秀尔算法(Shor’s algorithm)是一种非常著名的量子算法,可以说是量子计算的一块金字招牌了。秀尔算法可以在多项式时间内完成大整数质因数分解。所以,从诞生之日起,秀尔算法和RSA算法的矛盾,就不可调和。 秀尔算法不是通过暴力破解的方式找到最终密码的,而是利用量子计算的并行性,快速分解出公约数,从而打破了RSA算法的基础(即假设我们不能很有效的分解一个已知的整数)。同时,秀尔算法展示了因数分解这问题在量子计算机上可以很有效率的解决,所以一个足够大的量子计算机可以破解RSA。 RSA加密“曾经”之所以强大,是因为它对极大整数做因数分解的难度决定了RSA算法的可靠性。将两个质数相乘是件很容易的事,但要找到一个庞大数字的质数因子却非常困难。这便是大量现代科技的依靠之处,RSA加密就是凭借其简洁性迅速风靡。 经典大数分解和秀尔算法的复杂度对比
2001年,某IBM研究小组使用秀尔算法完成了 15 = 3×5 这个整数分解运算 。20年过去了,量子计算机暂时还没摧毁RSA。 参考资料 Hero@ACT防量子破解公链长图片段资料
私钥、公钥、地址的三位一体的关系
2.私钥签名和公钥验签(验证签名)的过程
—- 编译者/作者:MoMedia 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
重磅雄文:防量子破解及公链的巨大价值
2021-01-27 MoMedia 来源:区块链网络
相关阅读:
- 如今的FIL是否与十年前的比特币如出一辙?币价都在三位数十年后的F2021-01-27
- 行情分化第三阶段后期2021-01-27
- 逸戈谈币:1.27行情分析行情再度走出回调何时盘整完成打开新空间2021-01-27
- 比特币亿万富翁将竞选加州州长2021-01-27
- 严哥:比特币以太坊回调蓄力,市场终会被多头再度打开2021-01-27