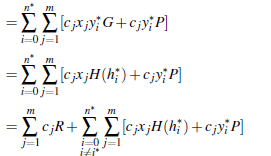【译文】MimbleWimble协议（二）

2.准备工作

2.1密码学原语

分组：总之，G1，G2将表示一种有效可计算双线性对的椭圆曲线组? e：G1×G2→GT，其中GT等于某些素数q，小正整数k的Fqk的乘法组。我们进一步要求G1和G2都具有素数阶r。设G，H是G1的固定生成元，其离散对数相对对彼此来说是未知的（也就是说，它们不是我的秘密（NUMS）点；G2不需要任何规范生成器。我们将根据需要对这些组进行计算难度假设。我们把模r的整数写成Zr，把所有组中的组运算写成+。

所有密码方案都有一个隐式GenParams（1λ）相位，在给定安全参数λ的情况下，该相位均匀地随机产生r、G1、G2、GT、G和H。

2.1.1标准原语

定义1：提交方案是一对算法Commit（v，r）→G，Open（v，r，C）→true，false}，使得Open（v，r，Commit（v，r））接受Commit域中的所有（v，r）。它必须满足以下安全属性。

?数据绑定：如果对于Commit域中的所有（v，r），Open（v'，r'，Commit（v，r））接受的没有（v'，r'）≠（v，r），则方案是绑定的。如果没有PPT算法能够产生具有不可负概率的（v'，r'），则它在计算上是有约束力的。

?隐藏：如果一致随机r的分布式Commit（v，r）对于不同的v值是（相等的，计算上不可区分的），则该方案是（完全的，计算上）隐藏的。

定义2：我们定义了一个同态提交方案，它的值参数是同态的。也就是说，对于v，v'的提交可以添加以获得对具有相同安全属性的v+v'的提交。

例1：将Pedersen提交定义为以下方案：Commit:Z 2 r→G将（v，r）映射到vH+rG，并打开：Z2r×G→{true，false}检查Commit（v，r）是否等于vH+rG。如果G中的离散对数问题是困难的，那么这是一个计算上有约束、完全隐藏的同态提交方案[Ped01]。

定义3：给定一个同态加密C，我们定义C上的范围证明作为C的提交值在某个给定范围内的密码证明[a，b]。我们进一步要求范围证明是提交的开放信息的零知识证明（zkPoK）。

除非另有说明，否则范围证明将提交到范围[0,2n]中，其中n足够小，以至于无法对任何实际数量的提交进行求和以产生溢出。

例如，我们可以使用[Max15]中描述的Pedersen提交的范围证明来满足这些标准。

2.1.2下沉签名

这给我们带来了Mimblewimble所需要的第一个新原语。

定义4：我们将下沉签名定义为以下算法集合：

?Setup（1λ）输出密钥对（sk，pk）；

?Sign（sk，h）取密钥sk和非负整数“height”h，其在λ中为多项式，并输出一个签名s。

?Verify（pk，h，s）接受公钥pk和签名s，并从{true，false}输出。

满足以下安全性和正确性：

?正确性：对于所有多项式h，（sk，pk）←Setup（1λ），s←Sign（sk，h），我们已经接受Verify（pk，h，s）。

?安全：设（?，pk）←Setup（1λ）。然后给定pk和一个oracle H，其中给定H返回Sign（sk，H），没有PPT算法A可以为所有给定给oracle的H生成一对（s，H'）和H'>H，并且Verify（pk，H'，s）接受。（除非概率可以忽略不计。）

“下沉签名”这一名称的动机是，给定高度h上的签名s，伪造者可以使用相同的公钥和h’≤h创建签名s‘在h高度上’，从而“降低”签名的高度。我们稍后将使用此功能来帮助Mimblewible链的可扩展性。

定义5：我们说下沉签名是可聚合的或可求和的，如果给定一个从Setup（1λ）计算出的pki值的线性组合pk，则si← Sign（ski，h）（对于固定h）的相同线性组合有可能计算签名s，以使Verify（pk，h，s）接受。

对于一个可求和的下沉签名，我们将上述安全对策推广到允许对方A以多项式多次并行博弈，并以其接收到的公钥的任意线性组合获胜。（它还必须提供线性组合的系数。）

定义6：我们提出以下可求和下沉签名（Poelstra，Kulkarni）。设H2是一个随机的oracle哈希，其值为G2。

?Setup(1λ )选择一个均匀随机的sk← Zr，并设置pk=sk?G。

? Sign(sk, x)首先计算序列{x0，…，xN}，其中x0＝x，xi＋1是通过从xi减去2的最大幂除以（即，通过清除其最不重要的1比特）来获得的。我们看到xn=0，n是1加上x中的1比特数，因此是O（log2x）。

最后，它输出s＝{sk?H2（xi }n i＝0）。

? Verify（pk，x，{si}）将S计算为所有si的总和，计算H＝∑ n i=0H2(xi)，并检查e（G，S）＝e（PK，H）。

请注意，验证步骤仅使用签名元素的和。但是，这些额外的数据稍后会有用，所以我们在这里声明它，这样我们就可以证明该方案是安全的。

方案的正确性和可求和性是直接的。

定理1：这是一个安全下沉签名概述，在以下意义：如果存在一个在定义5中描述对手A赢得游戏，可以解决计算co-Diffie-Hellman (co-CDH)问题（G2，G1）模拟器B存在，给定Oracle访问A。

证明：B回答对H随机的oracle查询，并按以下方式工作。（回想一下，定义5中的游戏是定义4中的并行游戏。）

我们假设，在对任何高度x进行签名查询之前，对手首先要对oracle的所有随机查询进行验证；同样，在对高度x?进行伪造之前，对手也要进行所需的查询。然后我们假设它总共最多请求qp次公钥，最多进行qh次随机oracle查询。

1.B从其挑战者那里接受co-CDH挑战（G，P，Q），其中G，P∈G1，Q∈G2，目标是产生R∈G2，使得?e（P，Q）=e?（G，R）。

2.B通过随机生成均匀键值对（xi，Pi）并用Pi+P应答来响应第i个公钥请求。

3.B通过生成一个一致随机键值对（yj，Hj）来响应第j个随机oracle查询，除了Hj? =Q（对于j?$← {1，…，qh}）并用Hi进行回复。

4.B对高度hk和公钥Pk的第k个签名查询的响应如下：它计算序列{hkn}，并检查H（hkn）值中是否有Q；如果是，则中止。否则，对于每个i{0，…，n}它知道一个zi，使得H（hki）=ziG并产生s={ziP}i。

5.最后，通过伪造一个由系数{ci}mi=1（并非所有ci为零）、一个公钥P?= ∑ m i=1 ci(Pi+P)、一个高度h?大于任何这样查询的h?、一个签名s?={Si}使得∑n*i=0e（G，Si）=∑n*i=0e（P*,H（H*i））。

6.如果某个H（H?i?）=Q，那么为了保持上述总和，为P?=x?G写x?，我们必须有，对于y*i 使得 H(h*i ) = y*i G

其中R是B的CDH挑战的解决方案，并且B可以计算每一个其他项。

为了完成这个证明，我们必须证明我们是以远离1的概率为界中止的，并且我们的获胜条件是以不可否认的概率发生的。我们发现只有当攻击者要求使用需要Q的签名时，我们才会中止，而如果Q用于攻击者的伪造中，我们就赢了。

如果H（h?）=Q（概率为1/qh，完成证明），则两者都会发生。

—-

编译者/作者：灰狼

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。