作者:?Igor Mandrigin 翻译:?阿剑 来源:以太坊爱好者 什么是 “无状态以太坊”? 如果您已经了解什么是 “无状态以太坊” 以及 “区块见证数据”,可以跳过这一段。 为执行交易及验证区块,以太坊网络的节点需要了解整条区块链的当前状态 —— 也就是所有账户和合约的余额和存储数据。这些数据一般来说是存储在 DB(数据库文件)里面的,在需要用于验证时才会加载到一棵默克尔树中。 无状态以太坊客户端的工作思路则稍有区别。顾名思义,无状态客户端就是不使用硬盘 DB 来执行区块(虽然客户端中可能也维持着完整的状态)。相反,无状态客户端依赖于 “区块见证数据(block witness)” —— 就是一段特殊的数据,它会跟相应的区块一起传播;拥有了这段数据,客户端就可以重建出一个(代表部分状态的)默克尔子树,该分支足可用于执行该区块中的所有交易。 你可以在这篇文章中读到关于无状态客户端的更深入的描述:https://blog.ethereum.org/2019/12/30/eth1x-files-state-of-stateless-ethereum/ 当然咯,需要传播区块见证数据就意味着无状态客户端的网络要求要比普通节点更高。
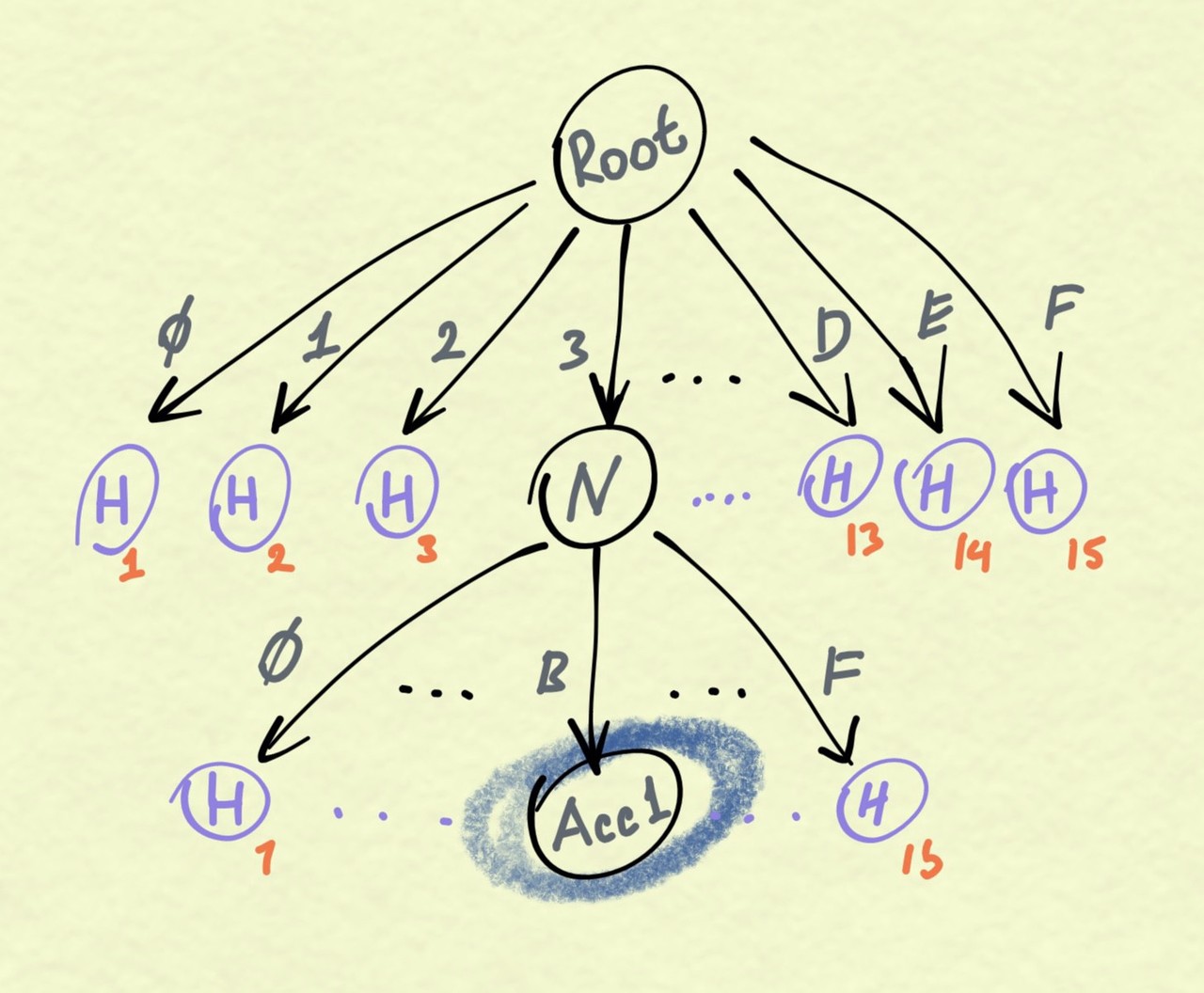
-见证数据大小折线图(区块高度 500 万到 850 万)- 现在人们已经提出了很多降低见证数据规模的思路:使用 有效性/计算完整性 证明(包括但不限于零知识证明)、加入更多的压缩手段,等等。其中一种办法是将以太坊的默克尔树(即用来表示以太坊的默克尔树)从十六进制转为二进制。 这就是本文想要探讨的问题。 为什么要使用二进制树 默克尔树的一大优良特性是,验证树根值(就是一个哈希值)正确与否并不要求你具有整棵树所有的数据。只需把所有省略的非空路径替代为相应的哈希值就可以可。 那么使用十六进制默克尔树有什么不好呢? 设想整棵树都已填满数据(即树上的节点已几乎没有为零的子节点)。要验证一个区块,我们只需要一小部分默克尔树节点的数据。那么,我们只需把其他路径的数据替代为哈希值就可以(让这棵子树变得可以验证)了。 但是,每多加入一条哈希值,区块见证数据就会大一些。 如果我们转变为二进制默克尔树,这个问题就可以得到缓解 —— 因为默克尔树上的每个节点都只有两个子节点,所以至多只有一个字节点需要被替换为哈希值。(换句话来说,我们可以更早地开始 “切割” 默克尔树的路径,因为我们的粒度是 1 比特,而不是十六进制下的 4 比特。) 这样做也许能大幅降低见证数据的规模。 我们再举例说明一下。 假设执行某个区块只会影响一个账户:3B 路径下的 Acc1(二进制为 0011 1011)。整棵树是全满的(树上的节点没有为零的子节点)。
-二进制状态树与十六进制状态树的比较- 如果说二进制状态树看起来有点吓人,那只是因为二进制树我画全了,但没有把十六进制树的所有代之以哈希值的节点都画出来。 来数个数: 为创建出一棵二进制状态树,见证数据需要包含 8 个哈希值,7 个分支节点和 1 个账户节点。也就是见证数据中有 16 个元素。为创建出一棵十六进制状态树,我们只需 1 个分支节点,1 个账户节点,但需要 30 个哈希值。也就是有 32 个元素。 所以,假设哈希值和分支节点在区块见证数据中的所占的空间是一样大的(其实哈希值所占的空间要更大一点),在我们的例子中,使用二进制树所需的见证数据大小只有十六进制下的一半。看起来不错。 那么,理论上就是这样。 我们来看看实际情况是如何。我们直接拿以太坊主网的数据来看看吧。 开始实验 先说最紧要的:我们怎么知道自己构建出来的区块见证数据是有用的呢? 测试方法如下:我们使用区块见证数据来生成一棵默克尔子树,在这棵树上运行相应区块中的所有交易,然后校验结果是否与我们所知的一致。只要交易都能成功执行(Gas 够用,轨迹相同(they have the same traces),等等),我们就可以断定这个见证是足够充分的。
-测试方法:1. 执行区块;2. 从状态树中抽取出见证数据;3. 使用见证数据构造出一棵子树;4. 禁用 DB 访问、使用子树来执行区块(具体可见 github)-其次,我们需要一些基准数据(用于比较)。因此,我们也使用 500 万到 850 万高度的区块、在十六进制默克尔树模式下生成了见证数据,并将见证数据大小的统计数据存在一个超级大的 csv 文件中。 我们尝试的第一步是执行完一个区块后就组装出一棵十六进制树,然后将它转为二进制树,再从这棵二进制树中提取出见证数据。 这种方法有几个好处:易于实现,而且验证 十六进制-二进制 的转换也很简单。 不过,我们遇到了两个问题,而且其中一个还不小。 第一个,正如我们上面证明的那样,比起二进制树,十六进制树包含更多的账户节点,如果我们先生成十六进制树再转换,得到的结果就跟在二进制树模式下直接生成所得到的见证数据不一样。 为什么呢? 因为十六进制树数据总是以 1/2 字节的速度增长,而二进制树总是以 1 比特的速度增长,因此键(key)的长度可以是奇数位。 实际上,见证数据中还包含一些额外的扩展节点(EXTENSION node),它们还要稍微大一点。不过即便对内容较多的区块(包含约 5000 条交易的区块),体现在见证数据大小上的差别也非常之小(小于 5%)。 关键的是性能。随着树的规模增长,转换的速度会越来越慢。 用更具体的数字来说明一下:在我们的 Google Compute Engine 虚拟机上,处理速度约为每秒 0.16 个区块,也就是每分钟处理小于 10 个区块,处理 100 万个区块要超过 3 个月! 所以,我们决定采取更复杂的办法,开发出一个原生使用二进制默克尔树的实验性分支。也就是说,我们要把 turbo-geth 代码库例地所有十六进制状态树全部替换为二进制树,然后区块就是基于二进制树来执行的了。 这种办法的不利之处在于,部分哈希值的校验只能被忽略掉(区块根哈希,有些时候的账户存储树根哈希,因为我们的区块链快照机制有所欠缺)。 但主要的验证机制还是一样的:我们需要能够使用二进制树来执行区块、从见证数据中创建出默克尔子树。 再来谈谈 key。 为简化起见,我们对 key 的编码方式是非常低效的:1 byte per nibble;一个 key 的每一比特就要占用 1 字节。这样做大大简化了代码层面的改变,但区块见证数据中的 ”key“ 部分会是我们使用 bitset 时候的 8 倍大。 因此,在进一步分析中,我会假设 key 的编码方式是最优的(使用 1 比特来编码 1 比特的信息)。 Hex vs. Bin:结果 我的分析分为两段,总共分析了以太坊主网上的 200 万个区块。 区块高度 500 万到 650 万 我在这个 github 库里面提供了使用 python 脚本来重复这一实验的命令行:https://github.com/mandrigin/ethereum-mainnet-bin-tries-data 首先我们来分析一下数据集。 python percentile.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust  -一个箱型图,箱体显示上四分位到下四分位之间的数据,左右延伸出去的线条显示上 1% 到下 1% 之间的数据(即排除了极端大和极端小的 1% 数据) python xy-scatter-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust  - XY 散点图(已假设 key 以最优方式编码)(横轴为 Hex 下见证数据大小,纵轴为 Bin 下见证数据大小)- 可以看出,二进制见证数据的大小总是优于十六进制树下的见证数据。 我们再加入另一个参数,用二进制见证数据大小除以十六进制见证数据大小,看看我们得到了怎样的提升。 python size-improvements-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust 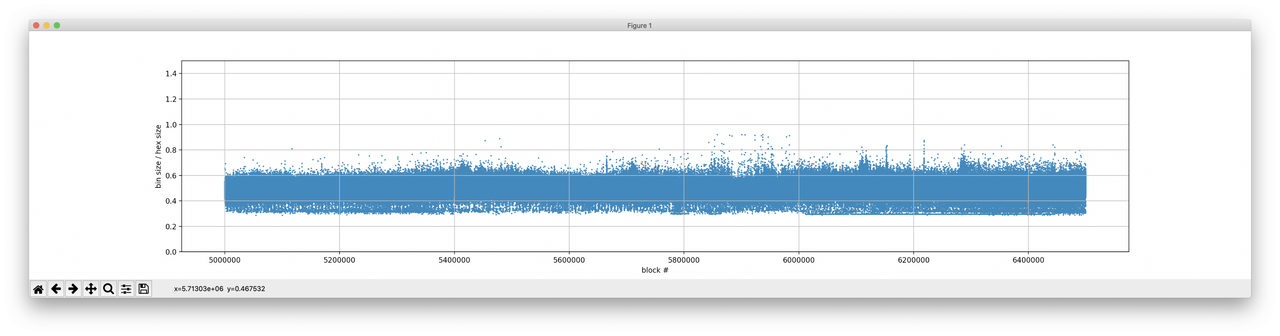 -二进制见证数据的大小/十六进制见证数据的大小(值越小越好)- 为更好地理解这张图标,我们也输出了平均值和百分位值。 平均值 = 0.51 (平均来说节省了 49% 的空间) P95 = 0.58 (按节省程度排列,对于前 95% 的数据,至少节省了 42% 的空间) P99 = 0.61 (按节省程度排列,对 99% 的数据,至少节省了 39% 的空间) 在实际场景中这意味着什么? 对于 99% 的区块,见证数据的大小可以降低至少 39% 。 对于 95% 的区块,见证数据的大小可以降低至少 42% 。 平均来说,见证数据可节省 49%。 我们也要考虑见证数据大小的绝对值。为使数据变得可读,我们每 1024 个区块取滑动平均值。 python absolute-values-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust 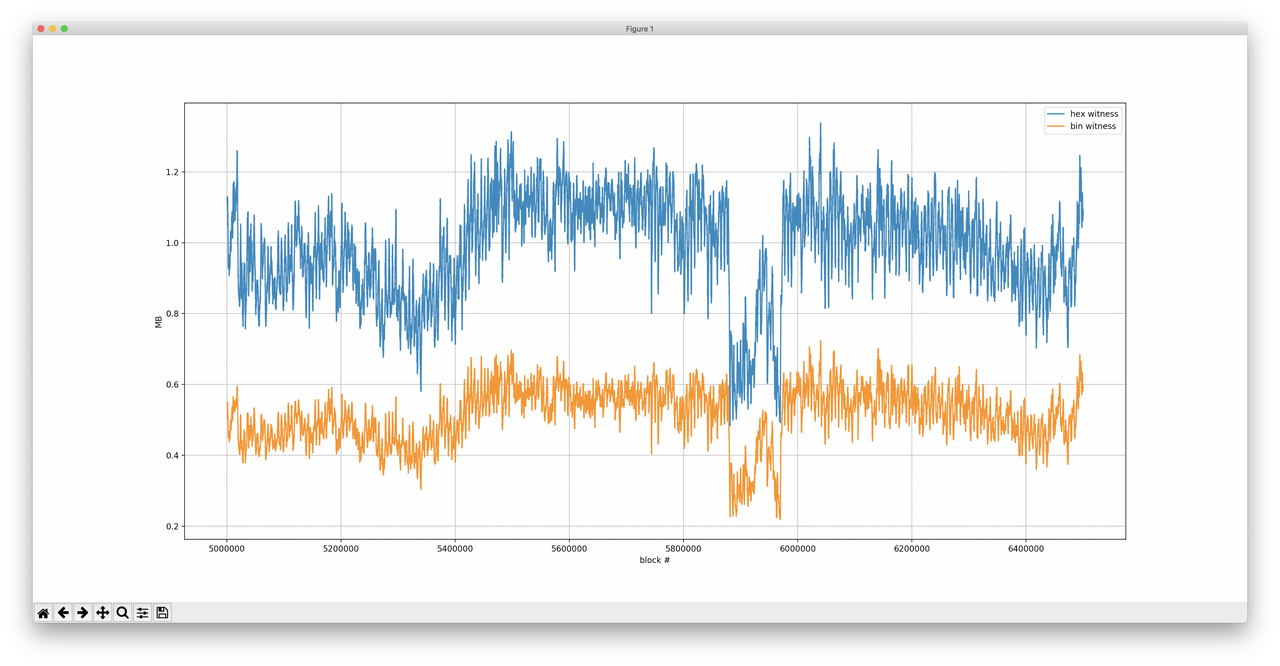 -依时间顺序绘制的见证数据大小折线图,纵轴单位为 MB- 再来看看最新区块的情况。 区块高度 800 万到 850 万 python percentile.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust  -箱型图,箱表示上下四分位以内的数据,线表示上下 1% 以内的数据- python xy-scatter-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust 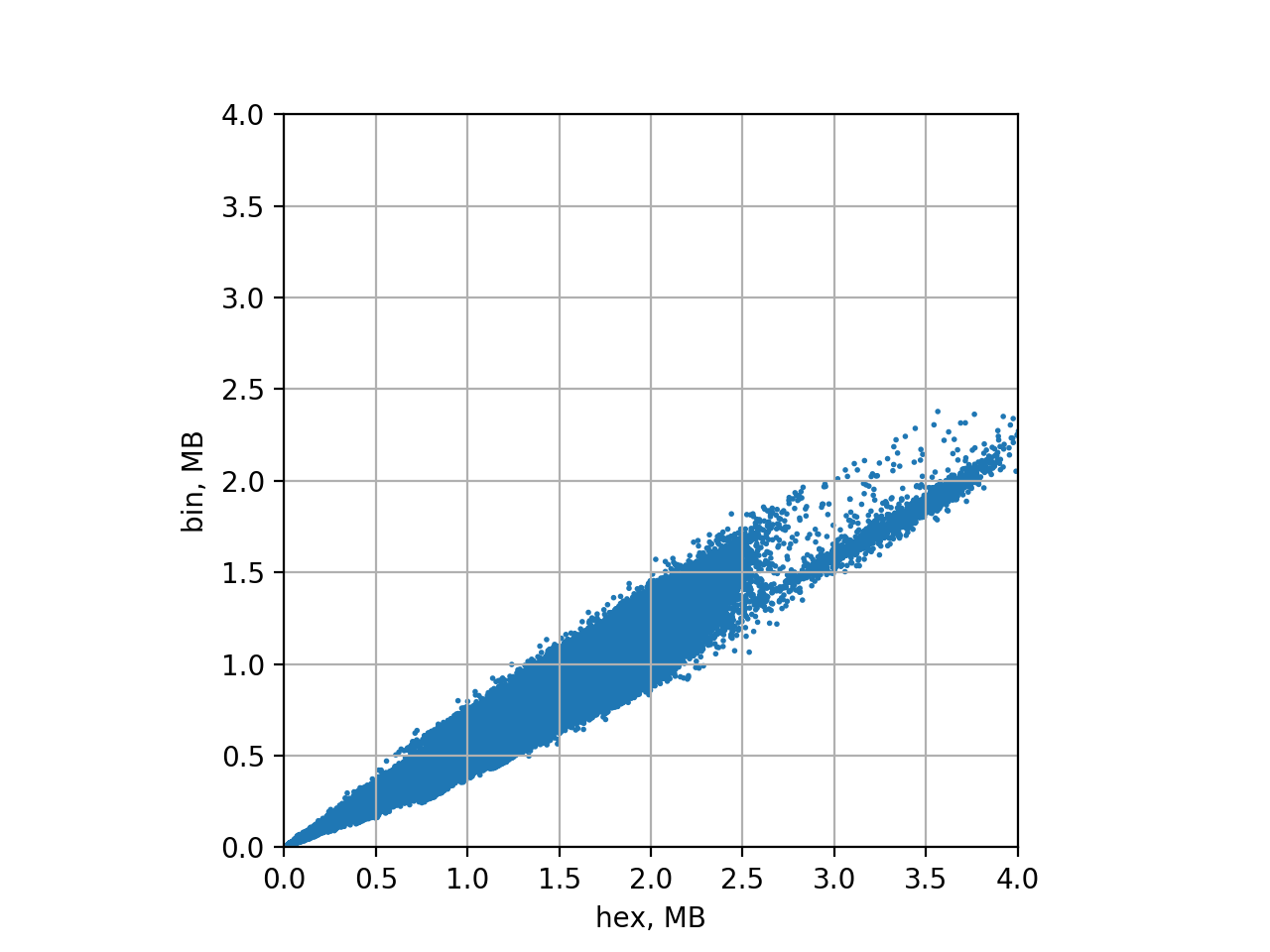 还有规模上的节约。 python size-improvements-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust  - XY 散点图(已假设 key 以最优方式编码)(横轴为 Hex 下见证数据大小,纵轴为 Bin 下见证数据大小)-平均值 = 0.53 (平均来说节省了 47% 的空间) P95 = 0.61 (按节省程度排列,对于前 95% 的数据,至少节省了 37% 的空间) P99 = 0.66 (按节省程度排列,对 99% 的数据,至少节省了 34% 的空间) 最后,再来看看见证数据的绝对大小。 python absolute-values-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust  -依时间顺序绘制的见证数据大小折线图,纵轴单位为 MB- 结论 在使用以太坊主网数据做过测试以后,我们可以看到,切换为二进制树模式可以大幅提升生成见证数据的效率(见证数据大小平均减少 47-49%)。 另一个结论是,这种提升并没有理论上那么显著。原因可能在于主网区块的实际数据(比想象中要复杂)。 也许,通过分析一些例外情况(也就是二进制树所得提升最少的情况),我们可以知道更多优化见证数据规模的办法。 试着使用别的原始数据来跑跑 GitHub 中的脚本吧:https://github.com/mandrigin/ethereum-mainnet-bin-tries-data (完) —- 编译者/作者:以太坊爱好者 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
观点 | 无状态以太坊:二进制状态树实验
2020-01-10 以太坊爱好者 来源:区块链网络
LOADING...
相关阅读:
- 于集鑫:8月1日BTC/ETH晚间分析及操作策略2020-08-02
- 陈楚初:日内比特币以太坊再创新高后续多单思路保持不变2020-08-02
- 于嘉硕:8.1比特币以太坊还会涨吗?晚间怎么操作2020-08-02
- 比特币上涨突破17000刀时计算接下来的行情里面主涨趋势还有几波?2020-08-02
- 情绪指标显示比特币仍被低估,比特币跌破$ 11,5002020-08-02

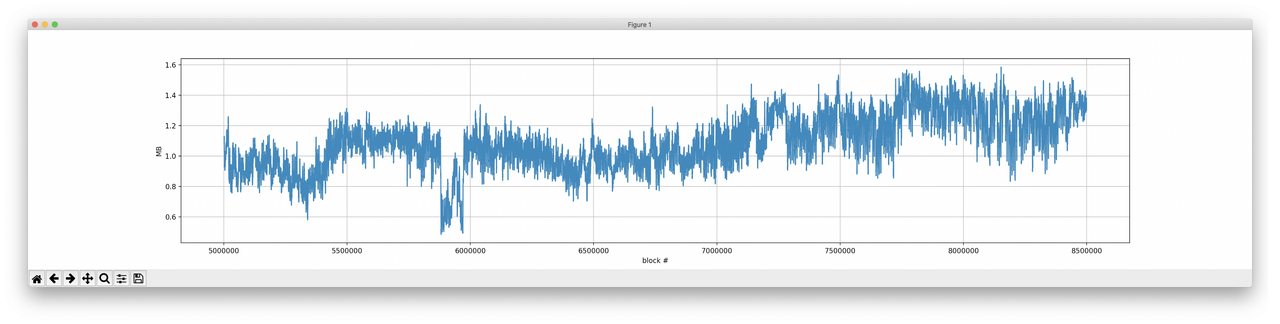


 -百分比分析(单位为 MB)-现在我们可以生成一些很酷的图表了!
-百分比分析(单位为 MB)-现在我们可以生成一些很酷的图表了!
 - 800 万号到 850 万号区块的百分位分析-
还有 XY 散点图。
- 800 万号到 850 万号区块的百分位分析-
还有 XY 散点图。