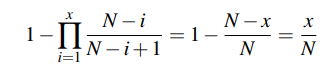【译文】MimbleWimble协议（五）

3.3共识

Mimblewimble使用哈希缓存[Bac02]类型的区块链，其中区块链中的每个区块都被称为其难度的权重标记。如果困难D的每个块都有一个哈希到哈希总空间的1/D大小范围内的头，则区块链是有效的。我们定义了一个从块A到块B的有向边，前提是A在其头部提交到块B，并要求每个块提交到其唯一的父块。

我们可以在共识历史的第3.2节中完善我们的定义，将其定义为以根为终点的最高加权路径。这和比特币的设计是一样的。

3.3.1区块头

在本文中，我们还将块上的第二个图结构定义为顶点，称为紧凑区块链。我们迭代定义紧凑型区块链如下。

1.创世区块位于紧凑型区块链中。

2.创世纪后的第一个区块被添加到紧凑区块链中，并被分配与其难度相等的有效难度。

3.每个新块都添加到紧凑型区块链的顶端，并可能导致块从紧凑型区块链中移除，如下所示：

（a） 首先，其有效难度计算如下。考虑块的“最大可能难度”m，它是由块的哈希分隔的哈希空间的大小。（这可能比实际困难要大。）

有效难度是从块的难度开始，然后从顶点开始，将尽可能多的连续块的有效难度相加，使总难度小于或等于M。

（b） 在上述计算中使用有效困难的所有块体，除了新块体本身外，都从紧链上落下。

紧凑型区块链通过将每个区块提交到当前紧凑型链中所有区块的merkle和树（很难有效地求和数量）来编码在真正的区块链中。

接下来，我们将证明几个定理，以直观地给出紧致区块链的特性。

引理2：生成具有有效难度D的块所需的预期工作相当于计算D哈希；类似地，生成具有总有效难度D的多个块时，必须完成计算D哈希的预期工作。

证明：就在随机预言模型中。

定理5：替换紧凑链中的块B（即生成总难度大于或等于且紧凑链不包含B的区块链）的预期工作量大于或等于替换非紧凑链中的B、B的父链、父链的父链等所需的工作量，直至不包括B的父链。

证明：这紧接着引理2，并且每个块的有效难度被定义为大于或等于跳过块的难度之和。

Corallary1：生产紧凑型区块链所需的预期工作量至少与生产包含相同区块的完整链所需的预期工作量相同。

定理6：假设难度恒定，给定长度为N的区块链，则紧凑链的预期长度为O（logN）。

证明。紧凑链的定义使得[BCD+14，附录A]中的证明仍然有效。我们总结如下：

1.首先，考虑从顶端开始向后扫描，直到我们找到一个块，它可以跳过所有剩余的块回到创世区块。建造这个区快将在紧凑区块链中。在我们检查的第一个x块中存在这样的块的概率是

所有1≤x≤N的期望值是（N+1）/2，也就是说，我们希望这一跳能把链长度减半。

2.总的来说，我们可以从顶端向后扫描，直到在上一步中找到一个跳回该区块的区块。这将使（预期中的）剩余的链减半，以此类推。

我们重复这个过程直到没有块可以跳过是紧凑链的长度，因为每一步都会在紧凑链上增加一个块，并且每一步都会将剩余的块数减半，我们看到只有对数级的多个步骤。

我们发现难度的微小变化不影响这种证明的特性，因此，持续难度的情况可以被视为对现实情况的很好的近似。

定理7：给定一个区块链B（为了这个定理的目的，我们认为B仅仅是最多工作路径），只有一个紧凑链C?B。此外，只要给定C的区块以及紧凑链中每个区块向前一个区块提交的开始，验证者可以确定C是紧凑链。最后，B\C中的块不会出现在B的任何扩展的紧凑链中（即，一旦块被丢弃，就可能永远被遗忘）。

证明：通过构造，存在一个紧凑链C，它是B的一个子集，假设B的一些其它紧凑链C′≠C也存在。设C←为从C′和C中包含的顶端开始的最长路径（由于顶端本身构造在C′和C中，这是非空的），设β为C←的最深块。

现在，β前面的块在C和C′中必须不同；然而，这是不可能的，因为β提交给紧凑链中先前块的有序Merkle和树，“前面的块”必须是第一个β的哈希不够小而不能跳过的块，这是由Merkle和树的形状唯一指定的。我们的结论是C'=C。

接下来，我们认为当B被扩展时，没有B\C块被添加到紧凑链中。但这是迫在眉睫的，因为通过建造，只有新的区块才会被添加到一个紧凑链中。

3.3.2已证实和预期的工作

然而，虽然可以计算出预期的工作是相同的，但一般来说，紧凑链并不像全链那样证明有足够的工作。在这里，通过“证明一个工作量”，我们的意思是，一个少于这个工作量的证明者产生链的可能性微乎其微。例如，考虑一个跨越n个区块的总难度为D的区块链，其紧凑链具有logn个区块。

假设攻击者试图在εD工作中生成此链，其中0<ε<1。这就要求，平均来说，每个单独的块都要在预期时间内产生。每个块的产生时间是一个独立的变量，因此切诺夫界证明可以让我们更精确地逼近这一点：如果ε＜1，则概率随链中块的数目呈指数级衰减。

对于全链，这意味着概率O（exp[（1-ε）n]（n为指数）；对于紧凑链O（exp[（1-ε）logn]）或O（n 1-ε）（n为次线性）。事实上，极端情况甚至更糟：一个紧凑链可能只包含一个有难度D的块，在这种情况下，概率仅为O（exp（1--ε））。这意味着攻击者愿意花费整个链工作的某个固定百分比，无论链的长度如何，成功重写链的概率都是相同的。

为了保守起见，我们得出结论，本文所描述的紧凑链证明没有工作【6】。

【6】这并没有提到如[KLS16]中描述的紧凑型SPV证明，该证明在紧凑型证明的长度上设置了下限，以便上限低于预期的工作攻击者能够成功的概率。我们不能采用这种方法，因为我们在共识代码中使用这些证明，因此需要定理7。

那么它们有什么好处呢？在Mimblewimble中，我们期望一个链的验证者从最近的两个月开始要求所有的块，比如说，从那里到开始就要求一个紧凑链（在第3.3.3节中，我们将看到如何只用紧凑链来进行完整的验证）。合成物将：

?可伪造，预期工作等于整个链的工作；但是

?仅证明最近两个月的工作

与比特币（Bitcoin）不同，在比特币中，打造区块链的预期工作与其经验证的工作是相同的（渐进的），在Mimblewimble中，这些数量是不同的。预期的工作会影响激励机制：理性的参与者会选择延长最长的工作链，而不是像比特币那样尝试伪造；另一方面，经过验证的工作会影响核查者对世界状况的确定性：他们知道至少已经做了两个月的工作来制作他们看到的链，这不是一个意外，如果这是一个伪造品，这是一个非常昂贵的，不能可靠地重复。

3.3.3下沉签名与紧凑链

在这一节中，我们描述了下沉签名如何与紧凑链相互作用，特别是我们发现仅使用紧凑链就可以进行完整的Mimblewimble验证。我们引入了块的紧凑有效性概念，它弱于定义14中描述的有效性。尽管如此，我们保留了第1.2节的信任模型。

为此，我们修改了先前块的Merkle和树以及它们的有效难度，使之不仅对难度求和，而且（a）块事务的超额（定义7），（b）该超额上的下沉签名。多余的值作为点以明显的方式加起来，但是下沉签名更加复杂。

我们不是直接添加签名，而是在Merkle树的每个节点上组合来自每个子节点的签名集，方式如下：对于任何区块高度x，让{xn}表示定义6中定义的递减序列。然后，节点上的签名集是其子签名集的并集，除了当集合中出现两个高度x<y使得{xn}?{yn}时，这两个签名都将被删除，并由通过添加原始签名的相应组件而获得的{xn}上的签名替换。

因此，对于高度为h的块，Merkle和树的根向其祖先块提交将具有O（logh）下沉签名，在0到h之间，每2次方一个。

有了这个结构，我们就可以定义块的有效性。

定义16：区块是紧凑有效的如果

?它在定义14的意义上是有效的。

?其Merkle和树将达到第3.3.1节规则允许的最深区块。

?在遵守所有总结规则的意义上，这一提交是有效的。

?上述提交将是一个Merkle证明，包括从提交到{ci，c'i}形式的Merkle根的路径，其中c'是直接提交到区块；因为所有i c'i是ci的Merkle树中的兄弟；ci+1是对{ci，c'i}的提交。我们要求第一个c'i是树中的一个右兄弟，在它上面有一个有效的下沉签名集。（如果没有这样的c'i，那么这个块将跳回创世区块，因此我们要求树根的所有签名都是正确的。）

定义17：区块是完全有效的如果他是紧凑有效的并且

?它向全链中的前一个提交（树中提交的多余/签名与前一个块匹配）。

?它在创建时对当前UTXO集有有效提交。

（后一个条件允许仅使用紧凑链验证UTXO集；它还防止共识攻击，即用户被赋予相同的链，但其提交的UTXO集不同。前一个条件确保压缩块的内容与完整块的内容没有区别，只要完整的验证器在监视。）（如果没有人在监视，则这仍然是一个没有意义的点。）

定义16的条件是非常技术性的。我们可以简单地总结如下：当一个高度为h的块跳回到h’时，我们将每个中间块的签名下沉到可能大于h'的最低高度，然后将所有在同一高度上结束的签名聚合起来。这种混乱的Merkle和树只显示了如何由验证器检查这个条件，只要给出多段的数据。

我们认为这种设计保留了信任模型。特别地：

定理8：不重写出现中的块（尽可能多地工作），就不能删除任何事务。

证明：每一笔交易在其出现的区块的高度h上都有一个下沉签名。当从紧凑链上移除一个块时，上述结构可能会导致只有在下沉到某个较低高度h'后才能验证该特征。

然而，由于h'总是被保证位于h所做的紧凑链中相同的两个块之间，因此除了重写这两个块中最近的一个块之外，不能删除该签名。然而，通过构造，这就要求工作大于或等于重写事务最初出现的块。

定理9：定义16所要求的提交在整个链的高度上占O（log3）空间。

证明：提交包含Merkle树的对数多个节点，每个节点包含对数多个下沉签名，每个签名的大小都是对数的。

—-

编译者/作者：灰狼

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。