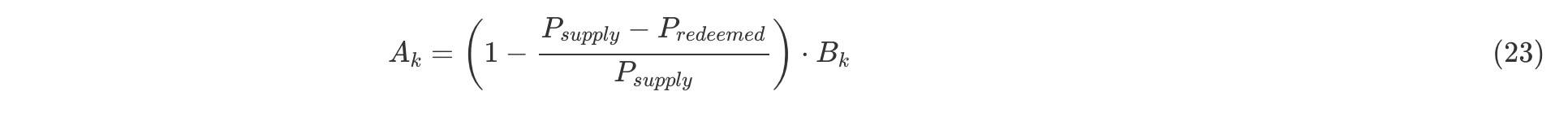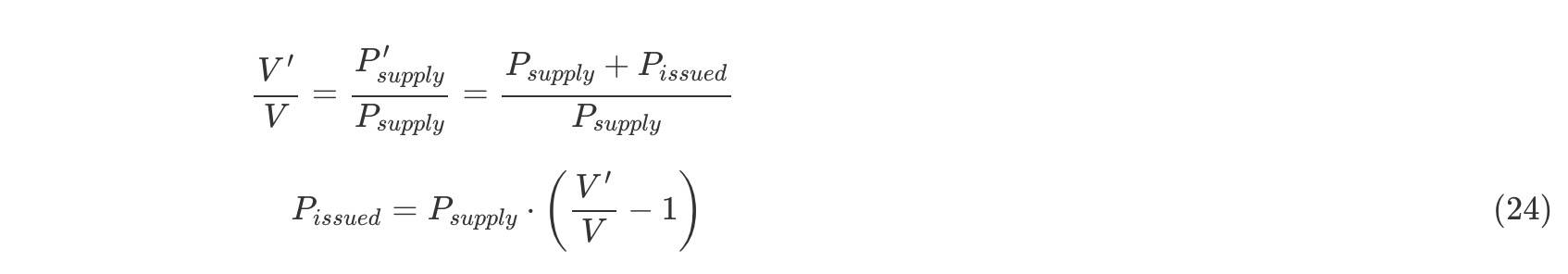写在前面:DeFi赛道的竞争已开始升温,尽管像Maker、Compound这样的老牌DeFi项目依旧占据了优势,但越来越多的挑战者正在涌现,而Balancer正是其中一个潜力股,你可以将自己的稳定币放入该协议池中,从而获得相比使用Compound更高的收益,原因在于,你不仅能从贷款利息中获得收益,还能因为提供流动性而获得交易费收益,此外,它还能避免无常损失。 那它又是如何实现的呢?我们不妨通过Balancer的白皮书来具体了解它的设计。
目录 1、介绍 2、理论 2、1 值函数 2、2 即期价格 2、3 有效价格 2、4 即期价格证明 2、5 恒定值分布证明 2、6 交易公式 2、6、1 Out-Given-In 2、6、2 In-Given-Out 2、6、3 In-Given-Price 2、7 流动性提供公式 2、7、1 所有资产的存取款 2、7、2 单资产存/取款 3、实例 3、1 License 3、2 发布 3、3 数值算法 3、4 受控池与最终池 3、5 Swap和退出费用 4、参考文献 一、介绍 指数基金是一种常见的金融工具,历史上第一只指数基金诞生于1972年。从那时以来,投资者们在很大程度上依赖于不同的投资组合策略来对冲风险。 指数基金保证投资者在一个投资组合中有一个稳定的、可控的风险敞口。如果其中一项资产表现不佳或表现出众,则可以选择出售或购买策略,以保持其在总投资组合中的价值份额不变。 无论是在传统金融体系还是在区块链环境下,指数基金和其他类型的投资组合,都会向投资者收取管理费用,这些费用主要是用于覆盖再平衡投资组合的成本。 然而,投资组合管理和指数基金投资通常是采用的中心化解决方案,因此这类项目都具有某种形式的托管风险。 而Balancer协议是一个具有某些关键属性的自动做市商(AMM),这些属性使其可作为一种自平衡加权投资组合和价格传感器。 Balancer颠覆了指数基金的概念:你无需向投资经理支付费用来再平衡你的投资组合,而是向交易员收取费用,交易员通过跟踪套利机会来再平衡你的投资组合。 Balancer基于一个特定的N维曲面,该曲面定义了Balancer资产池中任何一对代币的成本函数。这种方法首先由Vitalik Buterin提出[1],并由Alan Lu概括[2],然后被流行的Uniswap 应用[3]证明是可行的。 我们应用Zargham等人[4]描述的基于不变量的建模方法来构造该解决方案,并将证明这些恒值做市商拥有这一特性。 二、理论 在这篇文章中,我们使用术语“代币”(token)来指代通用资产,因为我们的第一版实现是在以太坊网络上进行ERC20代币操作的合约系统。然而,以太坊的执行环境并没有使该做市算法成为可能的基础。 2、1 值函数(Value Function) Balancer交易函数的基础,是通过将值函数V(池权重和余额的函数)约束为一个恒定值而定义的一个曲面。 我们将证明,该曲面意味着每个点的现货价格,这样,无论进行什么交易,资产池中每个代币的价值份额都保持不变。 这个值函数V定义为:
其中 t代表资产池中的代币范围;Bt是池中代币的余额;Wt是代币的归一化权重,因此所有归一化权重之和为1; 通过使V恒定,我们可以定义一个不变值曲面,如下图所示。
2、2 即期价格(Spot Price)
资产池中的每对代币都有一个即期价格,该价格完全由该对代币的权重和余额定义。任何两个代币之间的即期价格,
其中:
Bi是代币i的余额,进入池中的交易者会出售该代币;Bo是代币o的余额,交易者会从池中购买该代币;Wi是代币i的权重;Wo是代币o的权重;
从这个定义可以很容易地看出,如果权重保持不变,那么Balancer资产池提供的即期价格只会随代币余额的变化而变化。如果池的所有者不向池添加代币或从池中删除代币,则代币余额只能通过交易进行更改。恒定曲面会导致交易者购买的代币(token o)价格上升,交易者出售的代币(token I)价格下降。我们可以证明,每当外部市场价格与Balancer池提供的价格不同时,套利者将通过与该资产池交易获得最大利润,直到其价格等于外部市场的价格。当这种情况发生时,就没有更多的套利机会了。这些套利机会保证,在一个理性的市场中,任何Balancer池提供的价格与市场其他部分能够同步移动。
2、3 有效价格
重要的是要记住,
如上所述,当交易金额趋于0时,EP趋向于SP:
首先,我们知道交易者在购买的东西Ao,是从合约余额中减去的,因此,Ao = ?ΔBo。同样,交易者卖的东西Ai,是合约余额的一部分,因此,Ai = ΔBi。 代入等式2和等式3,我们得到:
根据定义,该限制是减去Bi在Bo函数中的偏导数:
根据等式1中的值函数定义,我们可以分离出Bi:
现在,我们使用等式7来展开等式6中的偏导数:
这得出了我们要的证明。
2、5 恒定值分布证明
我们现在将证明:
Balancer资产池中的所有代币保持恒定的值份额;并且这些值份额等于和每个代币关联的权重;
让我们计算 从等式2我们可以计算
我们知道,以代币t表示的总池值,是以代币t表示的每个代币的值之和:
现在要计算Sn(每个代币n在池中所代表值的份额),我们要做的就是将每个代币n的值
这不仅证明了每个代币所代表的总池值份额是恒定的,而且还等于该代币的权重。 2、6 交易公式 如果我们认为值函数必须保持不变(即V在任何交易前和交易后必须具有相同的值),那么为任何给定的Balancer池计算交易结果将很容易。 但实际上,由于交易状态转换后有了交易费用,这导致V会增加。有关费用的更多详细信息,请参见实例:互换(Swap)和退出(Exit)费用章节内容。 2、6、1 Out-Given-In 当用户发送代币i以获得代币o时,所有其他代币余额保持不变。因此,如果我们将Ai和Ao定义为代币i和代币o的交换数量,则可以计算用户在发送Ai时获得的Ao数量。 已知交易后的值函数应与交易前的相同,我们可以这样写:
2、6、2 In-Given-Out 对于交易者来说,知道他们需要发送多少输入代币Ai才能获得期望的输出代币Ao,也是非常有用的。类似的,我们可以根据Ao的函数计算Ai,如下所示:
注意,公式11所定义的Ao在Ai<<Bi时趋向于 2、6、3 In-Given-Price 出于实际目的,打算使用我们的合约进行套利的交易者,希望知道代币i – Ai的数量,他们必须将这些数据发送到合约中,以将当前即期价格 期望的即期价格通常是外部市场价格,只要合约即期价格与外部市场价格不同,任何套利者都可以通过与合约交易,并使合约价格接近外部市场价格来获利。 套利者可能获得的最高利润,是当他们将合约即期价格精确调整到外部市场价格时。如前所述,这是我们的设计成功跟踪市场价格的主要原因。当在区块链上实施它时,这使其成为可靠的链上价格传感器。 可以证明用户需要与代币o进行交易的代币i–Ai的数量,以便资产池的即期价格从
资产池可以聚合多个不同用户提供的流动资金。为了使它们能够自由地从资产池中存取资产,Balancer协议引入了资产池代币的概念。资产池代币表示池中包含的资产的所有权。资产池代币的未偿供应量与池的值函数成正比。如果资产存款增加了10%的池值,则资产池代币的未偿供应也增加了10%。这是因为存款人(depositor)获得了10%的新资产池代币作为存款回报。 有两种方式可以将资产存入池中,以换取资产池代币或赎回池代币: 加权资产存/取款;单资产存/取款; 2、7、1 所有资产的存取款 “所有资产”存款必须遵循资产池中现有资产的分配。 如果存款包含资产池中已存在的每种资产的10%,则值函数将增加10%,而存储人(depositor)将获得当前未偿还资产池代币供应量的10%。因此,要在现有P supply总供应量的情况下接收P issued资产池代币,需要为池中的每种代币存储Dk个代币k:
其中Bk是代币k在存款前的代币余额。 类似地,加权资产取款是一种反向操作,即池内代币持有人赎回其资产池代币,以换取池内每项资产的比例份额。在给定P supply的现有总供应量的情况下,通过赎回P redeemed资产池代币,可以从池中为每个池代币提取Ak数量的代币k:
其中Bk是代币k在取款前的代币余额。 2、7、2 单资产存/取款 当用户发现池中的资产分配很有趣,因而希望向池中提供流动性时,他们可能没有按照加权资产存款要求的正确比例拥有所有资产。 Balancer允许任何人通过将单个资产存放到共享池中来获取资产池代币,前提是该池中包含这一资产。 将单个资产A存入一个共享池,相当于按比例存入所有的池资产,然后出售更多资产A以收回存入的所有其他代币。这样一来,存款人(depositor) 最终只会花费资产A,因为其他代币的存款金额将通过交易返还。 用于将单个资产存放到共享池的资产池代币数量,可以从上面描述的值函数中导出。 单资产存款 资产池代币供应量的增加与值函数的增加成正比。如果我们将P issued定义为存款回报而发行的资产池代币的数量,那么:
其中V′是存款后的值函数,V是存款前的值函数。同时考虑到
假设单资产存款是在资产t中完成的,那么所有其他代币的余额在存款之后都不会发生变化。然后我们可以写:
如果我们将At定义为存放在资产t中的金额,那么资产t的新池余额为$$B’t = B_t + A_t$$。然后,我们可以代入并获得新池代币$P{issued}inreturnforasinge?assetdepositI_t$发行数量的最终公式:
单资产取款 当资产池代币的持有者希望赎回其资产池代币P redeemed 以换取单个资产t时,在资产t, At中取款的数量是:
其中Bt是取款前资产t的池余额。 事实是,使用上述定义的存款和取款公式,在不考虑任何费用的情况下,如果有人为P issued资产池代币存入At数量的资产t,然后将相同数量的资产池代币兑换成资产t,则他们将获得相同的初始At数量。 单资产存/取款交易费 在单资产t的情况下,向共享池存款或从中取款,相当于对池中所有其他资产的存款额交易(1?Wt)。存入金额的Wt以资产t的形式由资产池持有,因此对其收取交易费用是不公平的。 实际上,如果我们忽略任何可能的资产池退出费,仅存入资产i,并立即提出资产o,由此产生的交易费用,与使用池提供的交易函数,从i到o进行的交易相同。 三、实例 关于Balancer的第一个版本实现,会有一些初始说明,我们将在发布源代码的同时发布一个更详细的系统说明。 3、1 以太坊平台上的免费软件 Balancer是以GPL3许可的以太坊智能合约系统实现的。 3、2 发布 Balancer协议会有3阶段发布计划,其中第一个称为青铜版本。青铜版本强调审计和代码清晰性,但没有对gas成本进行好的优化; 白银版本将带来很多gas优化和架构改进工作,这些更改将减少交易开销,并为受控池提供更大的灵活性。 而第三阶段的黄金版本将引入几个新的功能,旨在将整个系统连接在一起。 3、3 数值算法 “理论”部分中的公式足以描述系统的功能规格,但对于EVM虚拟机而言,它们并不容易实现,部分原因是缺少成熟的定点数学库。 我们的实现结合了一些代数变换、近似函数和数值技巧的组合,来计算这些具有有界最大误差和合理gas成本的公式。 本节的其余部分内容将与青铜版本源代码同时发布。 3、4 受控池与最终池 “青铜版本”的发行,允许资产池的两种基本信任层: 可通过“控制者”地址配置的受控池(Controlled?pool)。只有“控制者”地址才能向池中添加或移除流动性(调用join或exit)。这种类型的资产池允许更改池资产类型及其权重。注意,由于控制者是一个地址,它在原则上可以实现任意逻辑,比如以类似于最终池的方式管理公共存款。关键的区别在于,官方工具不会将其视为一个“无需信任”的资产池。随着“白银版本”的发布,具有更高信任要求的受控池将成为可能。最终池(Finalized pool)具有固定池资产类型、权重和费用。至关重要的是,这使得join和exit能够以安全、无需信任的方式公开访问,同时保持最小的实现。 3、5 Swap和exit费用 “青铜版本”会在两种情况下收费:(1)当交易者(通过swap及其变体)交换代币,以及(2)当流动性提供者(通过exit及其变体)从池中移除其流动性时。 这两种费用都可以由控制者配置,但当池最终确定时,它们也是固定的。 100%的swap费用会分配给流动性提供者,即每个资产池代币可赎回的基础代币数量会增加。 大部分的exit费会退还给留在资金池中的流动性提供者。 其余的exit退出费将转移到Balancer Labs公司控制的帐户中,用于开发未来的版本。
1.Vitalik Buterin: Let’s run on-chain decentralized exchanges the way we run prediction markets ? 2.Alan Wu: Building a Decentralized Exchange in Ethereum ? 3. https://uniswap.io/ ? 4. Zargham, M., Zhang, Z., Preciado, V.: A State-Space Modeling Framework for Engineering Blockchain-Enabled Economic Systems. New England Complex Systems Institute (2018) ? 本文链接:https://www.8btc.com/article/599680转载请注明文章出处 —- 编译者/作者:玩币族 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
指数基金破坏者?一文了解DeFi新锐Balancer
2020-05-22 玩币族 来源:区块链网络
LOADING...
相关阅读:
- ETH价格可能被低估||V神警告DeFi智能合约风险||YFII是中国人的DeFi2020-08-01
- 红包+精评活动,Defi赛道吸引资金追捧,oninbase考察上币名单有AMPL,它能2020-08-01
- 第630篇:李笑来说Defi最近还得出事……2020-08-01
- 市场总结:比特币推至$ 11,450,DeFi值现在锁定在$ 4B2020-08-01
- 为什么此DeFi交换是以太坊ERC-20代币的单程票?2020-08-01






 2、4 即期价格证明
现在让我们证明,V的选择需要公式2。
2、4 即期价格证明
现在让我们证明,V的选择需要公式2。




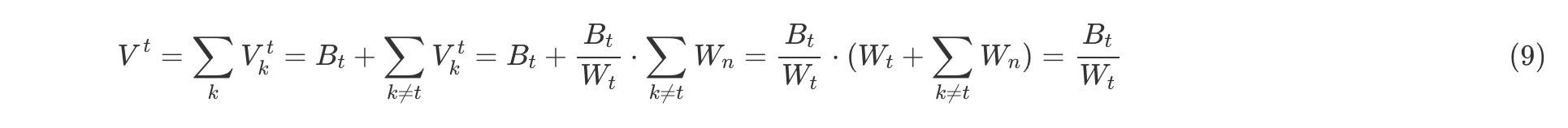



 2、7 流动性提供公式
资产池代币
2、7 流动性提供公式
资产池代币