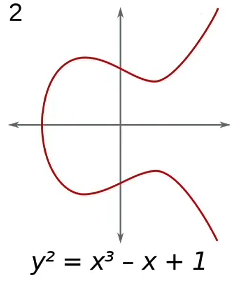EOS密码学：公钥生成原理-椭圆曲线加密算法

上一篇文章介绍了私钥的生成过程，私钥本质上是随机生成的。公钥是在私钥的基础上通过算法生成的。

私钥可以推出公钥，但无法从公钥推出私钥。

非对称加密

密码学中的加密方法主要有对称加密（Symmetric-key algorithm）和非对称加密（Asymmetric-key cryptography）。

比特币和EOS的公私加密算法就是一种非对称加密，具体使用了椭圆曲线加密算法。

椭圆曲线加密算法

公钥加密有ECC、ECDH、ECDSA等算法，第一个是椭圆曲线加密（Elliptic Curve Cryptography）的缩写，后两个算法是基于它的算法。

比特币和EOS的的公私加密算法使用的是ECDSA，全称是椭圆曲线数字签名算法（Elliptic Curve Digital Signature Algorithm），是使用ECC对数字签名算法（DSA）的模拟。

什么是椭圆曲线？

椭圆曲线是指满足下面公式的点集

其中a,b为实数，且4a3+27b2≠0（判别式）。

根据a,b系数取值的不同，它的函数图像大概像这样

椭圆曲线如何生成公钥？

以a=-1,b=1时的椭圆曲线方程为例

y2=x3-x+1

它的图像是这样的

使用椭圆曲线方程从私钥生成公钥的过程如下：

这里的相乘是椭圆曲线乘法，私钥k和椭圆曲线上的点P相乘，相当于k个该点相加。

椭圆曲线乘法：kP = P+P+P+...+P（k次）

这里就要定义椭圆曲线的加法。

椭圆曲线加法：在椭圆曲线上取一点P(Xp,Yp)，再取一点Q(Xq,Yq)，连接P、Q两点作一条直线，这条直线将在椭圆曲线上交于第三点R，过R点作垂直于X轴的直线，将过椭圆曲线另一点（一般是关于X轴对称的点），则该点被定义为P+Q的结果。

当P=Q时，P、Q两点的连线是曲线的一条切线，依然可以得到一个点P+Q，只是这个点比较远。

当P=Q时，P+Q=2P。

现在可以理解椭圆曲线乘法了，kP和2P只是倍数不同，kP表示重复椭圆曲线加法操作k次得到的曲线上的点，如上所述，这个点的坐标值拼接在一起就是公钥。

k是私钥，私钥本质上是一个随机的正整数，这个正整数可能是一个天文数字，即需要重复椭圆加法操作非常多次，那如何求出kP呢？

可以从P点（图上是G点）出发，不停做切线，找对称点，可以得到2P、4P、8P、16P...，这是指数级增长的，而k的最大值为2256，最多运算200多次即可求出kP。

为什么无法从公钥推出私钥？

从椭圆曲线生成公钥的算法得知，公钥只是椭圆曲线上的一个点，而这个点的来源可以有很多种，因而无法找到确切的私钥。

质数阶有限域上的椭圆曲线

椭圆曲线曲线上的点有无数个，如果选择一个很简单的点和私钥相乘，得到的公钥的安全性就会存在问题，因此对选取的起始点P(x,y)需要有一定的要求。

这个要求就是把椭圆曲线定义在质数阶有限域上，椭圆曲线上连续的点变成了离散的点。

质数阶有限域：实数范围上光滑的椭圆曲线在密码学应用上并不合适，需要进行有限域下的离散化操作才能使用。

对有限域上的离散点进行P+Q运算的原理和在连续曲线上相同，P、Q点的连线相交于第三点R，即为P+Q=R（因为是有限域，连线不会跑出边界，而是从边界对称点重复绘制）。

质数阶的大小决定了有限域的返回，这个质数越大，算出的公钥越安全。

secp256k1标准

比特币和EOS使用的椭圆曲线加密算法使用了secp256k1标准，这个标准规定具体使用那种椭圆曲线，具体规定如下：

1、系数a=0,b=7，即具体使用的椭圆曲线方程为y2=x3+7，在实数域上的图像如下（但这个图像不能用，需要质数阶有限域上的点）

2、质数阶为2256-232-29-28-27-26-24-20，用十六进制表示为

FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

3、基准点G的坐标为

(79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798, 483ADA77 26A3**65 5DA4FBFC 0E1108A8 FD17B448 A6855419 9**7D08F FB10D4B8)

未压缩格式公钥（65字节）

基准点G就是上述的起始点P，因为基准点G是固定的，使用私钥和G点相乘就可以得到公钥。

公钥 K = k*G 是椭圆曲线上的一个坐标点，G是基准点（生成点）。

未压缩公钥取点K(x,y)的坐标值加前缀0x04拼接而成：

04 360c18aab0eabbd8b6b26ca8032c693ed1aab28da6eb1d0472eabd8e21233816 f6a8b41be315205daefba5648e947bc106f254f56b1a40d6190cec7b9f40813d

公钥的坐标的x、y点都是32字节的数据，加上前缀1个字节，总共是65字节。

压缩格式公钥（33字节）

公钥是方程y2=x3+7上的一个点，知道x坐标，可以求得y坐标，因此可以只存储公钥的x坐标。

压缩格式公钥是以0x02或0x03作为前缀，y是偶数使用02作为前缀，y是奇数使用03作为前缀。

03 360c18aab0eabbd8b6b26ca8032c693ed1aab28da6eb1d0472eabd8e21233816

非对称加密原理

现在回头来看非对称加密的原理。

基准点G是约定好的，可以看作一个常数，这个决定了K=k*G这个公式的单向函数性质

这两个性质可以分别应用于数据加密传输和数字签名。

1、数据加密传输

Alice有自己的公钥（Ka）和私钥（ka），Bob有自己的公钥（Kb）和私钥（kb），公钥是对外公开的，私钥仅自己知道。

从图表可以得出，Alice知道ka * Kb的结果，Bob知道kb * Ka的结果，即都知道自己的私钥和别人的公钥的乘积。

由K=k*G可以得出以下式子

ka * Kb = ka * kb * G kb * Ka = kb * ka * G

这两个数据是相等的，使用Alice的私钥和Bob的公钥加密的数据，可以被Bob用自己的私钥和Alice的公钥解开。

2、数字签名

假设Alice对数据m进行签名，可以用私钥ka和m相乘（群乘法），结果假设为

N = ka * m

N就是签名后的数据。

其他人验证数据时使用Alice的公钥Ka和m相乘

Ka * m = ka * G * m = G * N

G是常数，而ka * m = N，即Alice发布的签名后的数据，因此其他人可以在不知道m的情况下验证数据是由Alice签名的。

总结

到这里，介绍了如何通过椭圆曲线加密算法从私钥生成公钥，但这里生成的公钥和平时见到的EOS公钥有点不太一样

EOS6W8V9TguKRMWGrGKcfBPNAPSdk1asKL5QnwbFZV7fJyNMNRLN5

其实这个EOSXXX开头的公钥本质上应该叫做“EOS地址”，由于EOS增加了账户的概念，账户充当了地址的作用，这个“EOS地址”就变成了“EOS公钥”。

下一篇文章介绍如何从私钥运算出EOS公钥。

—-

编译者/作者：松果

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。