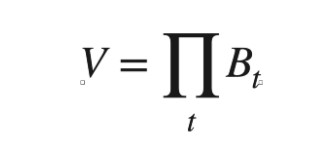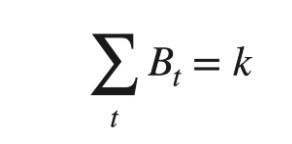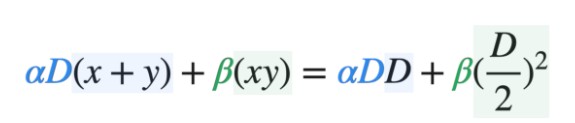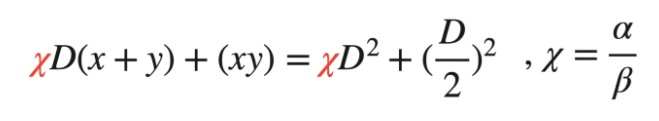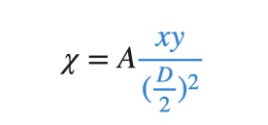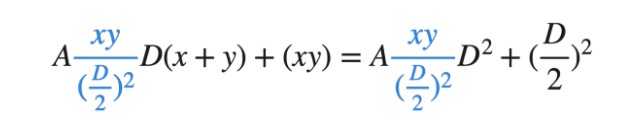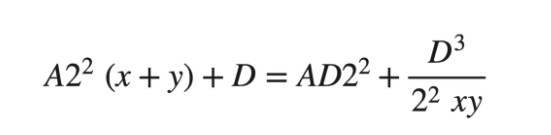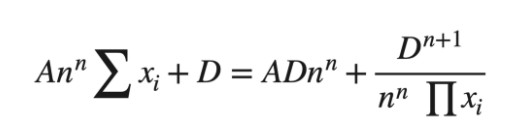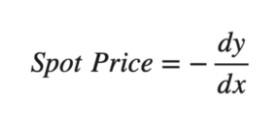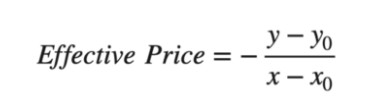稳定币为一种锚定法定货币价值的虚拟货币,可在这动荡的市场中作为相对可靠的避险资产。以美元为例,市场常见且流通性足够的美元稳定币就超过 3 种,每种的应用场景及背后的风险皆不相同,因而市场上产生了稳定币之间互换的需求。
稳定币稳定吗?
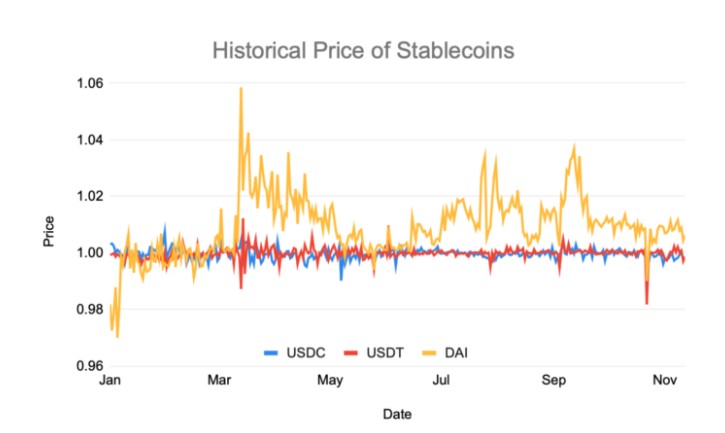
2020/1/1 至 2020/11/12 的稳定币价格走势图。 source: CoinGecko 由上图可见,稳定币其实不太稳定。
如何交换稳定币? 在 Balancer 建立资金池?
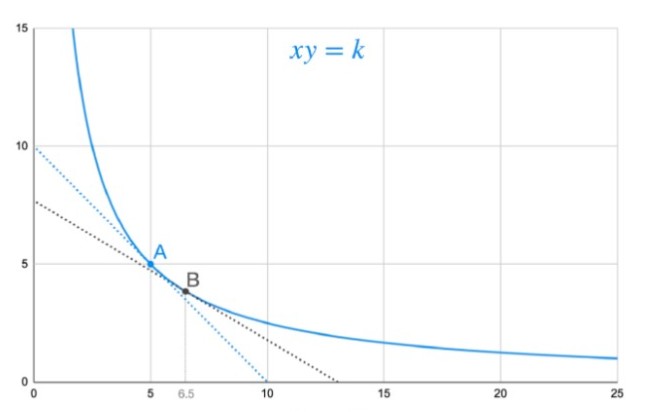
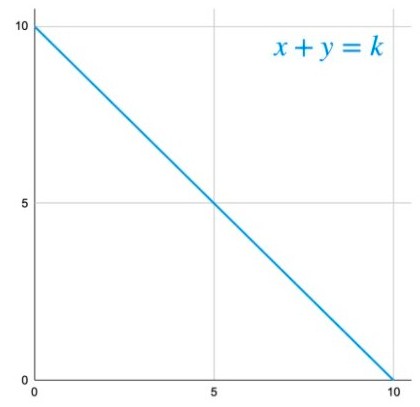
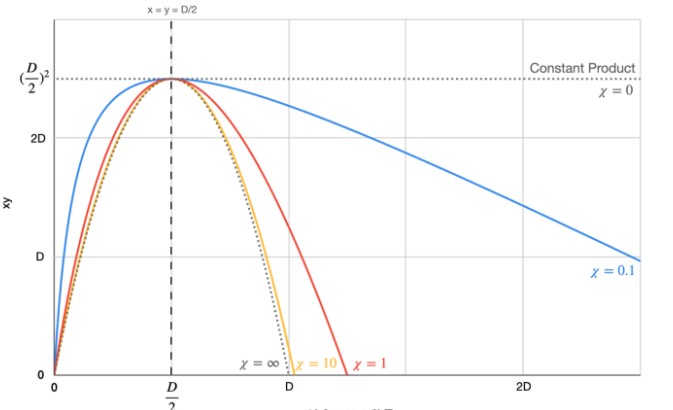
Balancer AMM 模型,设各币种权重相等 此模型称作恒定乘积做市商 (Constant Product Market Maker)。由于一次的互换仅与两个变数有关,其他变数可暂时当作常数。 为方便说明,假设 x 为池内 USDC 总量,y 为 池内 DAI 总量,将方程式作图如下:
现价等于该点切线之斜率(取绝对值) 图中 A 点位置为池内两个币种存量相等时,此时互换的比率为 1 : 1,对于稳定币来说是最理想的价格。但由于 Balancer 曲线的特性,一旦有人交易使蓝点移动后,价格就会明显改变。 举例来说,若有人卖出大量USDC ,使池内USDC 数量增加30%(A 点移至B 点),则价格会从1 DAI/USDC 掉至0.56 DAI/USDC,这对于稳定币来说几乎是不可能被接受的价格。
池内每种稳定币存量的总和为一定值 此模型称作恒定总量做市商 (Constant Sum Market Maker)。
以交换 USDC 及 DAI 为例 由于价格不会因供需而改变,因此当外部市场的稳定币间出现价差时,就会有人前来套利,直到其中一边的资金池枯竭为止,会使这些币种在池内失去流动性。
由上图可知,本该由五种稳定币组合而成的 mUSD,现在只剩下 USDC 及 TUSD 还有存量,其他币种皆被洗劫一空。
Curve 模型设计 Curve 以一些数学技巧,结合了上述两种模型的优点,以下将一步步推导,说明方程式怎么来的。
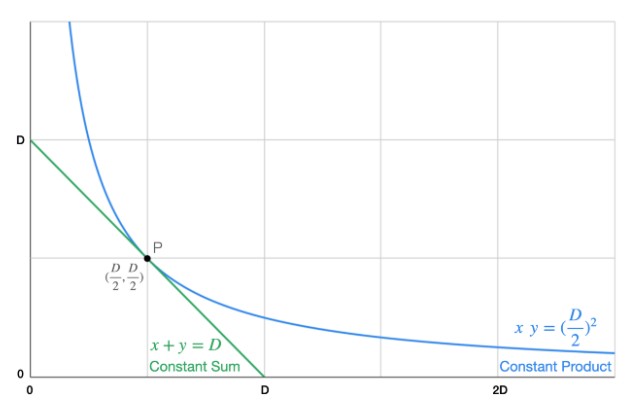
x(池内USDC数量),Y(池内DAI数量) P 点为两曲线之交点,此时 USDC 与 DAI 的存量皆为 D/2。将 P 点带入方程式即可求出两式之常数 k。 想要建构出介于两者之间的函数,最简单的方式就是对两式做加权平均。但由于二式的因次(Dimension,或称单位) 不同,所以相加时除了分别设权重为β 及α 之外,还要在下式多乘上D,使两式的因次皆为[数量×数量] 。
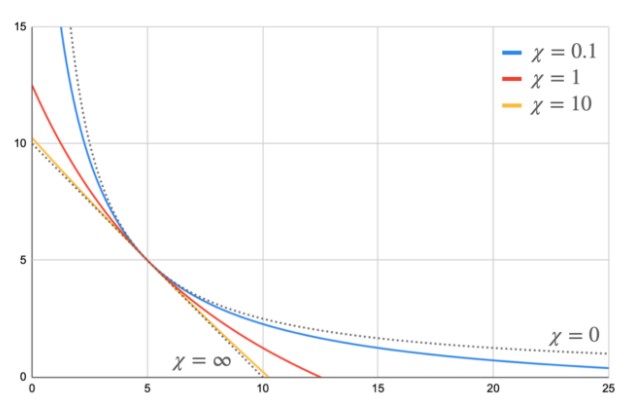
加权平均后之方程式 调整α 及β 的大小即可决定新函数的特性要偏向Constant Product 还是Constant Sum,但实际上真正决定新函数特性的是α 及β 的比例,因此我们可以将上式左右同除β ,并将α/β 设成χ。
接着简单分析一下权重大小对此函数的影响。
x(池内USDC数量),Y(池内DAI数量) 到目前这步,我们已经设计出一条曲线,能在价格为 1 : 1 的位置附近稳定价格,有效降低价格的波动,且能透过参数的调整决定价格变化的幅度。但此模型目前仍有个缺陷。若我们希望价格越稳定,则曲线会越接近直线,此时就会面临和mStable 一样的问题:一旦出现较大的价差时,池内其中部分币种可能会被掏空,出现只能卖无法买的局面,使池内流动性剧减。 这种情况不会发生在 Uniswap 或 Balancer 上,在 Constant Product 模型中无论币价如何波动,池内永远都会有币能交易。为达成类似效果,我们希望当池内资产存量偏离平衡点时,曲线能恢复成 Contant Product 的性质——也就是离平衡点越远时,χ 要越小。
横轴为池内 USDC 的数量 x,纵轴为 USDC 及DAI 的数量的乘积 xy。 上方虚线为 Constant Product 函数曲线的 xy 乘积,根据定义,该数值为常数。而 Constant Sum 函数及其他合成函数则是一条开口向下的曲线,该数值离平衡点越远会越小。
蓝色部分为动态参数,数值介于 0 与 1 之间 离平衡点越接近时,蓝色项越接近 1,函数调制效果最佳;
将此动态参数带入后方程式变为:
经整理后:
再将其绘成图:
x(池内USDC数量),Y(池内DAI数量);实线为动态参数,虚线为固定参数 由实线及虚线的比较可明显看出,在加上了动态参数后,偏离平衡点位置的将如同 Uniswap,永远都会存在一些些的流动性,池内资产不会归零。
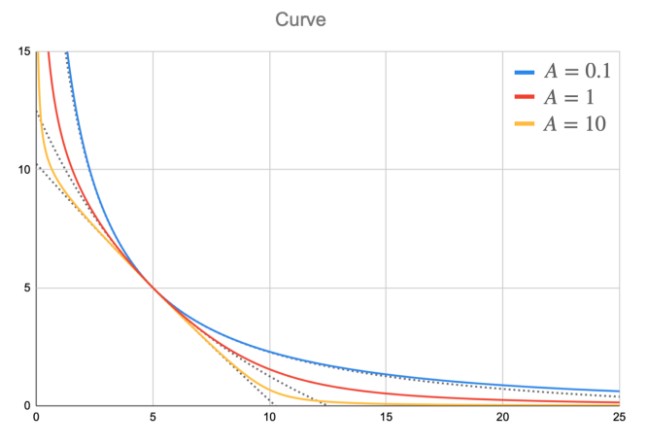
Curve 白皮书中的公式 终于,推导出 Curve 使用的公式了!
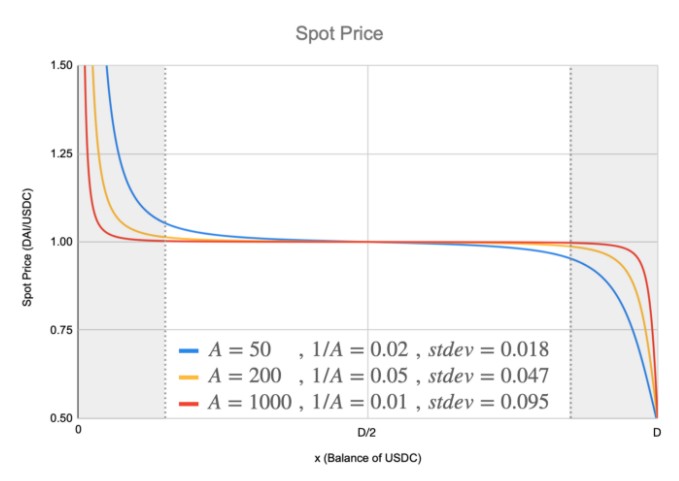
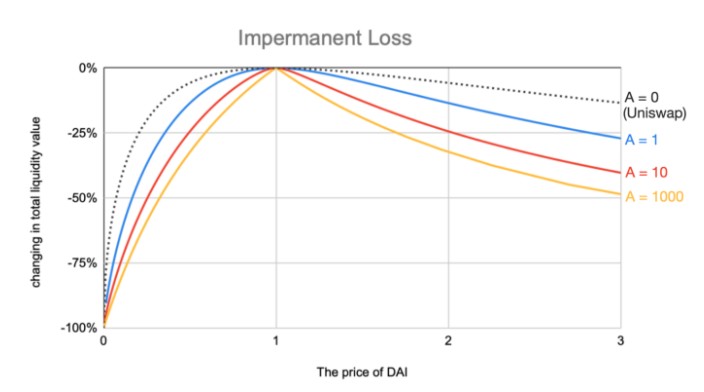
如前所述,A 为放大系数,决定曲线了价格在 $1 附近的稳定程度,A 越大越不容易滑价。那越不容易滑价越好吗?不尽然。滑不滑价其实并非重点。 以流动性提供者的角度或协议收入角度来看,最大化手续费收入才是首要目标。最大化手续费需要最大化交易量,因此决定 A 值时要考量的是池内币价的波动率。若池内币种锚定 $1 时常不太稳定的话,则要选择较低的 A 值,以免一旦波动出现,池内就会有币种近乎被掏空,导致交易量大减。
先将方程式写成 explicit function y=f(x) 的形式,再对其微分并加负号,即可计算出现价
此处假设了三种不同的 A 值,取样平衡点附近 ±70% 的资料点去计算价格的标准差。由图上的资料可看出,计算结果与 Michael 的描述相当一致,因此我们只要观察 A 值的大小,就能简单判断此池容许币价波动的程度。
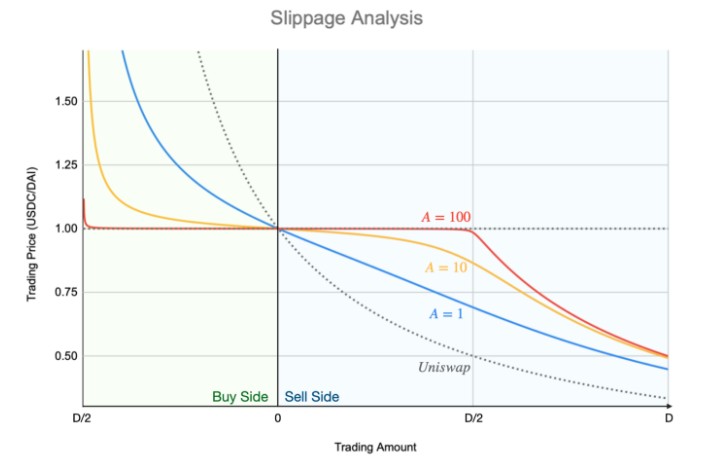
滑价 (slippage) 分析 滑价探讨的是一次交易使价格改变的程度,单笔交易的量体越大对价格的影响越大。一般而言,池内资产越多则价格越不容易变化。除此之外,Curve 还透过 A 值来调整曲线在 $1 附近的形状,放大了$1 附近的交易深度。
以上计算假设交易前池内各资产为平衡状态(也就是 x_0 = y_0 = D/2),再计算大额交易导致的价格变化。
如何吸引人增加流动性? 交易深度是交易所的根本,要有足够的深度才能降低滑价,以提供更好的交易环境。为了吸引资金投注提供流动性,Curve 提供了以下几种奖励作为诱因:
目前给个池的手续费皆相同。 source: https://www.curve.fi/compound 借贷协议及收益聚合器
以 Compound 池为例,该池部分 APY 收益源自手续费收入 + lending 利息。 source: https://www.curve.fi 值得特别注意的是,有些池虽然会将资金放到 Compound 中,但目前这两个 Compound 池无法领取 COMP,那些挖出来的 COMP 被永久的锁在合约内。 Curve Dev 已开发完成能领取 COMP 的新合约,目前在审计中。
CRV 奖励 网页上显示的 APY 为一个范围「+16.28% to 40.70% CRV」,实际能领取的数字取决于个人 CRV 的锁仓量与锁仓时间。以图上的例子来说,最低 APY 16.28%,经锁仓后最高可变为 2.5 倍的 40.70% 。
以 Compound 池为例,APY 的数字会根据 CRV 的现价即时调整。 source: https://www.curve.fi 为什么要有这么多种池? Curve 的数学模式允许池内存在任意数量的币种,那为什么不把所有的币都放到同个池子内,集中手续费收入呢?
由于 Curve 的 AMM 机制是强制让价格稳定于 1 美元附近,会无视外部市场对 USDT 的定价,所以当 USDT 归零时大家就会跑来 Curve 交易,把 USDT 换成其他仍具价值的稳定币。这会使池内其他稳定币近乎被掏空,只剩下大量的 USDT。如此一来,流动性提供者仅能换回大量且没价值的 USDT,将承受极大的损失。
BasePools u0026 MetaPools
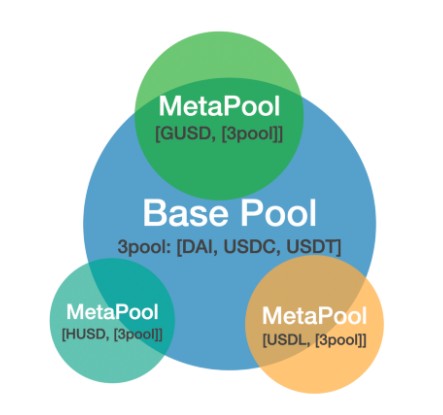
Base/Meta Pools 示意图(没按照实际资金使用比例绘制) MetaPool 是一种依附于 Base Pool 的池,可与 Base Pool 共享部分流动性,且有效分割风险。这样能在不直接稀释主流稳定币的情况下,替其他小币创造交易深度。目前 Curve 唯一的 Base Pool 为 3pool,由共识最强的三种稳定币 DAI、USDC 及 USDT 所组成。
优点:更高的收益 缺点:更大的风险
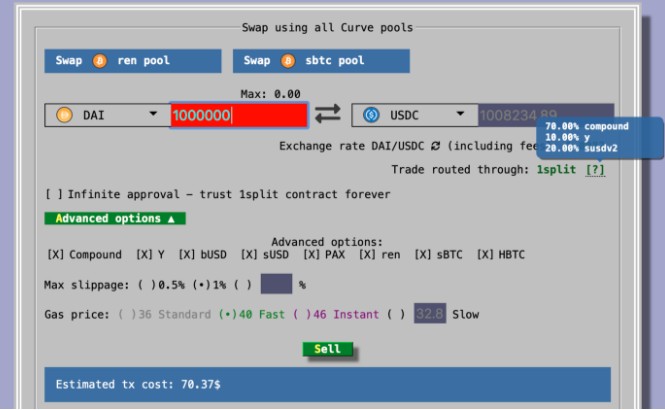
上方选取币种并输入数量;中间选择想互换的池;下方输入滑价上限及 gas fee。网页前端会自动计算出最划算的交易方式。 会有无常损失吗?
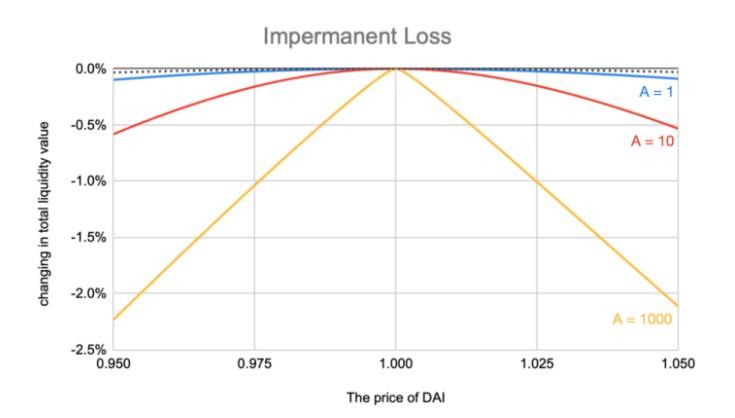
很小是因为:
由图可看出,在 A=1000 时,仅管币价 ±5% 波动,无常损失仍不会超过 -2.5%,该损失以目前的总体收益来说,回本赚钱绝对不是梦。 注意,此处分析仅为粗估,供数字数量级做参考。
让池内各个币种数量越平衡越好。
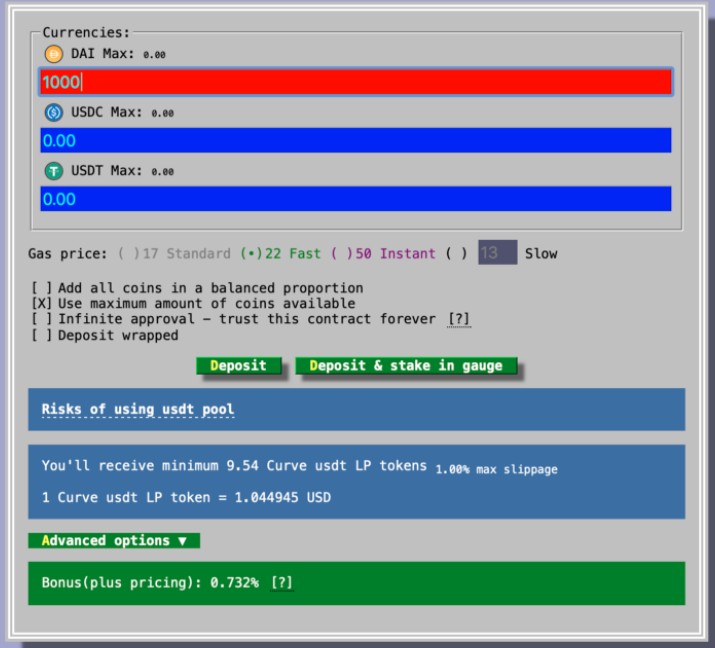
奖励为绿匡 (标注为 Bonus);滑价则为红匡 (标注为 Slippage) 以图上例子来说,因为池内 DAI 存量较少,所以存入 DAI 会有 Bonus 0.732%。此奖励并不是额外发放的,产生原因为目前 DAI 在池内价值高于 $1,因此存入 DAI 相当于将手上部分的 DAI 高价卖成更多的 USDC 及 USDT,此即收益的来源。而存入另外两种币相当于在低点出售该币种,会导致手上稳定币总量减少。
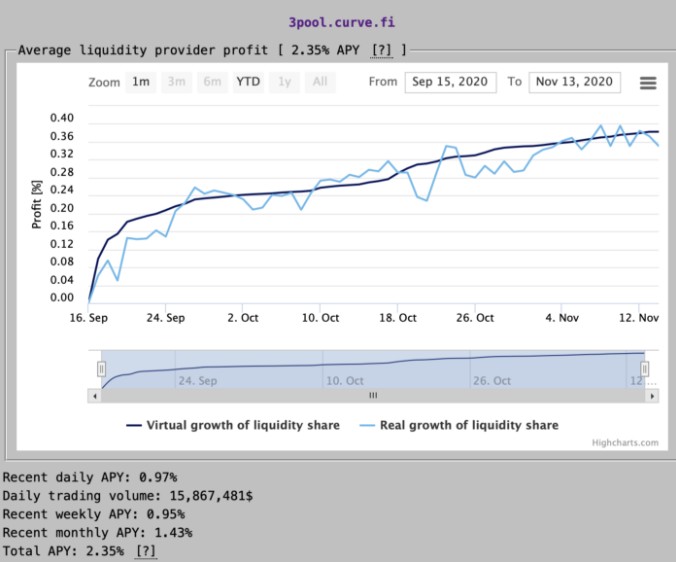
3pool 池内收益统计。 source: https://www.curve.fi/combinedstats 由上图统计表可看出,只要有人持续在交易,Curve 就能捕获价值以累积收益。蓝线收益以 real price 做计算,计价单位为 USDC。会上下震荡是由于池内稳定币的比例改变导致的价格浮动。黑线收益则是以 virtual price 做计算,该价格只涨不跌,且不随币价波动。代表的是当池内回到平衡状态时,每个 LP token 的价值。以数学是来表达即为:virtual price = D/(amount of LP tokens)。 结论 单以做市机制设计来说,Curve 是个相当优良的稳定币互换协议,是一个有效率的稳定币交换系统,能根据市场现况弹性的调整参数,更加完善了 DeFi 的世界。后记 做研究写文章的过程对我而言是相当有趣的,总能从中发现许多巧妙且聪明的机制设计,且还能以分散式、全自动的方式在以太坊上永续运行。原文链接:Establishing stable currency exchange mechanism: from balancer to curve —- 编译者/作者:洁sir 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
建立稳定币互换机制:从Balancer到Curve
2020-11-15 洁sir 来源:区块链网络
LOADING...
相关阅读:
- 币圈王哥:比特币低位筑底行情能否反弹成功2020-11-15
- 币圈丽姐:BTC/ETH多头渐暖凌晨能否再上16000高位2020-11-15
- BTC期权持仓量激增,交易者认为未填补的比特币期货缺口为1.8万美元2020-11-15
- 比特币年内涨超过400%涨幅牛冠全球资产2020-11-15
- 明杰论币:大饼跌势已成后续预计再难以登顶2020-11-15