ArkStream Capital:零知识证明四十年技术发展里程碑
时间:2024-07-30 来源:区块链网络 作者:区块律动BlockBeat
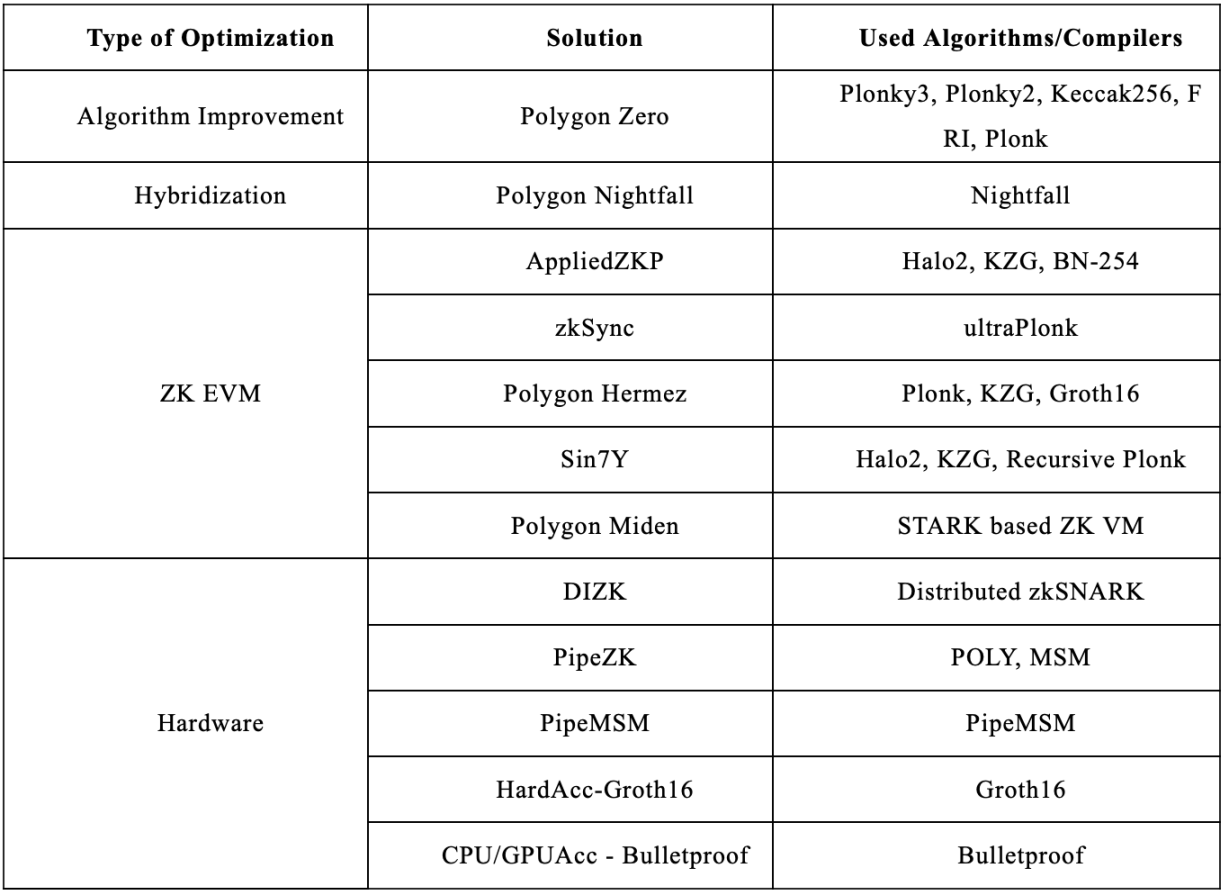
原文标题:《ArkStream Capital:零知识证明四十年技术发展里程碑》 原文作者:Ren,ArkStream Capital 摘要 零知识证明(ZKP)在区块链领域被广泛视为是自分布式账本技术以来最重要的科技创新之一,同时也是风险投资的重点领域。本文对零知识证明技术近四十年的历史文献和最新研究都做了系统的综述。 首先,介绍了零知识证明的基本概念和历史背景。然后,重点分析了基于电路的零知识证明技术,包括 zkSNARK、Ben-Sasson、Pinocchio、Bulletproofs 和 Ligero 等模型的设计、应用和优化方法。在计算环境领域,本文介绍了 ZKVM 和 ZKEVM,探讨了其如何提升交易处理能力、保护隐私和提高验证效率。文章还介绍了零知识 Rollup(ZK Rollup)作为 Layer 2 扩展方案的工作机制和优化方法,以及硬件加速、混合解决方案和专用 ZK EVM 的最新进展。 最后,本文展望了 ZKCoprocessor、ZKML、ZKThreads、ZK Sharding 和 ZK StateChannels 等新兴概念,并探讨了它们在区块链扩展性、互操作性和隐私保护方面的潜力。 通过分析这些最新技术和发展趋势,本文为理解和应用零知识证明技术提供了全面视角,展示了其在提升区块链系统效率和安全性方面的巨大潜力,为未来的投资决策提供了重要参考。 前言 在如今,互联网正在进入 Web3 时代的进程中,区块链应用(DApps)的发展迅速,几乎每天都有新的应用涌现。近几年,区块链平台每天都承载着数百万用户的活动,处理着数十亿笔交易。这些交易产生的大量数据通常包括用户身份、交易金额、账户地址和账户余额等敏感个人信息。鉴于区块链的开放性和透明性特点,这些存储的数据对所有人都是开放的,因此引发了多种安全与隐私问题。 目前,有几种加密技术可以应对这些挑战,包括同态加密、环签名、安全多方计算和零知识证明。同态加密允许在不解密密文的情况下执行运算,有助于保护账户余额和交易金额的安全,但无法保护账户地址的安全。环签名提供了一种特殊的数字签名形式,能够隐藏签名者的身份,从而保护账户地址的安全,但对账户余额和交易金额的保护则无能为力。安全多方计算允许在多个参与者之间分配计算任务,而无需任何参与者知晓其他参与者的数据,有效保护了账户余额和交易金额的安全,但同样不能保护账户地址的安全。此外,同态加密、环签名和安全多方计算无法在不泄露交易金额、账户地址和账户余额的情况下用于验证区块链环境中证明者是否拥有足够的交易金额(Sun et al., 2021)。 零知识证明是一种更全面的解决方案,这种验证协议允许在不透露任何中介数据的情况下验证某些命题的正确性(Goldwasser,Micali&Rackoff, 1985)。该协议不需要复杂的公钥设施,其重复实施也不会为恶意用户提供获取额外有用信息的机会(Goldreich, 2004)。通过 ZKP,验证者能够在不泄露任何私人交易数据的情况下,验证证明者是否具有足够的交易金额。验证过程包括生成包含证明者声称的交易金额的证明,然后将该证明传递给验证者,验证者对证明进行预定义的计算,并产出最终的计算结果,从而得出是否接受证明者声明的结论。如果证明者的声明被接受,意味着他们拥有足够的交易金额。上述验证过程可以记录在区块链上,没有任何伪造(Feige, Fiat& Shamir, 1986)。 ZKP 这一特性使其在区块链交易和加密货币应用中扮演核心角色,特别是在隐私保护和网络扩容方面,使得其不仅成为了学术研究的焦点,被广泛认为是自分布式账本技术——特别是比特币——成功实施以来最重要的技术创新之一。同时也是行业应用和风险投资的重点赛道(Konstantopoulos, 2022)。 由此,诸多基于 ZKP 的网络项目相继涌现,如 ZkSync、StarkNet、Mina、Filecoin 和 Aleo 等。随着这些项目的发展,关于 ZKP 的算法创新层出不穷,据报道几乎每周都有新算法问世(Lavery, 2024 ;AdaPulse, 2024)。此外,与 ZKP 技术相关的硬件开发也在迅速进展,包括专为 ZKP 优化的芯片。例如,Ingonyama、Irreducible 和 Cysic 等项目已经完成了大规模的资金募集,这些发展不仅展示了 ZKP 技术的快速进步,也反映了从通用硬件向专用硬件如 GPU、FPGA 和 ASIC 的转变(Ingonyama, 2023 ;Burger, 2022)。 这些进展表明,零知识证明技术不仅是密码学领域的一个重要突破,也是实现更广泛区块链技术应用——尤其是在提高隐私保护和处理能力方面——的关键推动力(Zhou et al, 2022)。 因此,我们决定系统地整理零知识证明(ZKP)的相关知识,以更好地辅助我们做出未来的投资决策。为此,我们综合审阅了关于 ZKP 相关的核心学术论文(依据相关性和引用次数进行排序);同时,我们也详细分析了该领域内领先的项目的资料和白皮书(根据其融资规模进行排序)。这些综合性的资料搜集和分析为本文的撰写提供了坚实的基础。 一、零知识证明基础知识 1. 概述 1985 年,学者 Goldwasser、Micali 和 Rackoff 在论文《TheKnowledge Complexity of Interactive Proof-Systems》中首次提出了零知识证明(Zero-KnowledgeProof,ZKP)和交互式知识证(InteractiveZero-Knowledge,IZK)。该论文是零知识证明的奠基之作,定义了许多影响后续学术研究的概念。例如,知识的定义是「不可行计算(unfeasiblecomputation)的输出」,即知识必须是一个输出,且是一个不可行计算,意味着它不能是简单的函数,而需是复杂的函数。不可行计算通常可以理解为是一个 NP 问题,即可以在多项式时间内验证其解正确性的问题,多项式时间指的是算法运行时间可以用输入大小的多项式函数来表示。这是计算机科学中衡量算法效率和可行性的重要标准。由于 NP 问题的求解过程复杂,因此被认为是不可行计算;但其验证过程相对简单,所以非常适合用于零知识证明验证(Goldwasser, Micali & Rackoff, 1985)。 NP 问题的一个经典例子是旅行商问题,其中要找到访问一系列城市并返回起点的最短路径。虽然找到最短路径可能很困难,但给定一个路径,验证这条路径是否是最短的相对容易。因为验证一个具体路径的总距离可以在多项式时间内完成。 Goldwasser 等人在其论文中引入了「知识复杂度」(knowledgecomplexity)这一概念,用以量化在交互式证明系统中,证明者向验证者泄露的知识量。他们还提出了交互式证明系统(InteractiveProof Systems,IPS),其中证明者(Prover)和验证者(Verifier)通过多轮互动来证明某个语句的真实性(Goldwasser, Micali & Rackoff, 1985)。 综上,Goldwasser 等人总结的零知识证明的定义,是一种特殊的交互式证明,其中验证者在验证过程中不会获得除语句真值外的任何额外信息;并且提出了三个基本特性包括: 1.完备性(completeness):如果论证是真实的,诚实的证明者可以说服诚实的验证者这一事实; 2.可靠性(soundness):如果证明者不知道声明内容,他只能以微不足道的概率欺骗验证者; 3.零知识性(zero-knowledge):在证明过程完成后,验证者只获得「证明者拥有此知识」的信息,而无法获得任何额外内容(Goldwasser, Micali & Rackoff, 1985)。 2. 零知识证明示例 为更好理解零知识证明及其属性,以下是一个验证证明者是否拥有某些私密信息的示例,该示例分为三个阶段:设置、挑战和响应。 第一步:设置(Setup) 在这一步,证明者的目标是创建一个证据,证明他知道某个秘密数字 s,但又不直接显示 s。设秘密数字; 选择两个大的质数 p 和 q,计算它们的乘积 。设质数 和,计算得到的; 计算,这里,v 作为证明的一部分被发送给验证者,但它不足以让验证者或任何旁观者推断出 s。; 随机选择一个整数 r,计算 并发送给验证者。这个值 x 用于后续的验证过程,但同样不暴露 s。设随机整数,计算得到的。 第二步:挑战(Challenge) 验证者随机选择一个位 a(可以是 0 或 1),然后发送给证明者。这个「挑战」决定了证明者接下来需要采取的步骤。 第三步:响应(Response) 根据验证者发出的 a 值,证明者进行响应: 如果,证明者发送(这里 r 是他之前随机选择的数)。 如果,证明者计算 并发送。设验证者发送的随机位,根据 a 的值,证明者计算 ; 最后,验证者根据收到的 g 来验证 是否等于。如果等式成立,验证者接受这个证明。当 时,验证者计算验证者计算,右侧验证 ; 当 时,验证者计算验证者计算,右侧验证。 这里,我们看到验证者计算得到的 说明证明者成功地通过了验证过程,同时没有泄露他的秘密数字 s。在这里,由于 a 只可以取 0 或 1 ,仅有两种可能性,证明者依靠运气通过验证的概率(当 a 取 0 时)。但验证者随后再挑战证明者次,证明者不断更换相关数字,提交给验证者,且总能成功地通过验证过程,这样一来证明者依靠运气通过验证的概率 (无限趋近于 0),证明者确实知道某个秘密数字 s 的结论便得到证明。这一例子证明了零知识证明系统的完整性、可靠性和零知识性(Fiat& Shamir, 1986)。 二、非交互零知识证明 1. 背景 零知识证明(ZKP)在传统概念中通常是交互式和在线的协议形式;例如,Sigma 协议通常需要三到五轮交互才能完成认证(Fiat& Shamir, 1986)。然而,在诸如即时交易或投票等场景中,往往没有机会进行多轮交互,特别是在区块链技术应用中,线下验证功能显得尤为重要(Sun 等, 2021)。 2.NIZK 的提出 1988 年,Blum、Feldman 和 Micali 首次提出了非交互式零知识(NIZK)证明的概念,证明了在无需多轮交互的情况下,证明者(Prover)与验证者(Verifier)仍可完成认证过程的可能性 。这一突破使得即时交易、投票以及区块链应用的实现变得可行 (Blum, Feldman & Micali, 1988)。 他们提出非交互式零知识证明(NIZK)可以分为三个阶段: 1.设置 2.计算 3.验证 设置阶段使用计算函数,将安全参数转换为公共知识(证明者和验证者均可获取),通常编码在一个共同参考字符串(CRS)中。这是计算证明并使用正确的参数和算法进行验证的方式。 计算阶段采用计算函数、输入和证明密钥,输出计算结果和证明。 在验证阶段,通过验证密钥来验证证明的有效性。 他们所提出的公共参考字符串(CRS)模型,即基于所有参与者共享一个字符串来实现 NP 问题的非交互式零知识证明。这种模型的运行依赖于 CRS 的可信生成,所有参与者必须能够访问相同的字符串。仅当 CRS 被正确且安全地生成时,依此模型实施的方案才能确保安全性。对于大量参与者而言,CRS 的生成过程可能既复杂又耗时,因此尽管这类方案通常操作简便且证明体积较小,其设置过程却颇具挑战 (Blum, Feldman & Micali, 1988)。 随后,NIZK 技术经历了迅猛发展,涌现了多种方法将交互式零知识证明转化为非交互式证明。这些方法在系统的构建或底层加密模型的假设上各有不同。 3.Fiat-Shamir 变换 Fiat-Shamir 变换,又叫 Fiat-ShamirHeurisitc(启发式),或者 Fiat-Shamir Paradigm(范式);由 Fiat 和 Shamir 在 1986 年提出,是一种能够将交互式零知识证明转换为非交互式的方法。该方法通过引入哈希函数来减少交互次数,并依托安全假设来保障证明的真实性及其难以伪造的特性。Fiat-Shamir 变换使用公共密码学哈希函数替代部分随机性和交互性,其输出从某种程度上可以视作 CRS。尽管此协议在随机预言机模型中被视为安全,但它依赖于哈希函数输出对不同输入的均匀随机性和独立性这一假设 (Fiat &Shamir, 1986)。Canetti、Goldreich 和 Halevi 在 2003 年的研究表明,虽然这种假设在理论模型中成立,但在实际应用中可能遇到挑战,因此在使用时有失败的风险 (Canetti, Goldreich & Halevi, 2003)。Micali 后来对此方法进行改进,将多轮交互压缩为单轮,进一步简化了交互流程 (Micali, 1994)。 4. Jens Groth 及其研究 Jens Groth 的后续研究极大推动了零知识证明在密码学和区块链技术中的应用。2005 年,他、Ostrovsky 和 Sahai 三人一起共同提出了首个适用于任何 NP 语言的完美非交互零知识证明系统,即使面对动态 / 自适应对手也能保证通用组合安全(UC)。此外,他们利用数论复杂性假设,设计了一种简洁高效的非交互零知识证明系统,显著减少了 CRS 和证明的体积 (Groth& Sahai, 2005)。 2007 年,Groth、 Cramer 及 Damg?rd 开始将这些技术商业化,通过实验验证,他们的公钥加密和签名方案在效率和安全性方面均有显著提升,尽管这些方案基于双线性群的假设 (Groth & Sahai, 2007)。2011 年,Groth 进一步探索如何将全同态加密与非交互零知识证明结合,提出了一种减少通信开销的方案,使得 NIZK 的体积与证明的见证大小保持一致(Groth, 2011)。在随后的几年里,他与其他研究人员对基于配对的技术进行了深入研究,为大规模声明提供了紧凑而高效的非交互式证明,尽管这些证明仍然没有脱离双线性群框架 (Bayer & Groth, 2012; Groth, Kohlweiss & Pintore, 2016; Bootle, Cerulli, Chaidos, Groth & Petit, 2015; Groth, Ostrovsky & Sahai, 2012; Groth & Maller, 2017)。 5. 其他研究 在特定应用场景中,特定验证者的非交互式零知识证明表现出了其独特的实用价值。例如,Cramer 和 Shoup 利用基于通用哈希函数的方法开发的公钥加密方案,在 1998 年和 2002 年有效地抵御了选择性密文攻击。此外,在密钥注册模型中,成功开发了一种新的非交互式零知识证明方法,适用于解决所有 NP 类问题,关键在于参与者需要注册他们自己的密钥以进行后续验证(Cramer& Shou, 1998, 2002)。 此外,Damg?rd、Fazio 和 Nicolosi 在 2006 年提出了改进已有 Fiat-Shamir 变换的新方法,允许在无需直接交互的情况下进行非交互式零知识证明。在他们的方法中,验证者首先需要注册一个公钥,准备后续加密操作。证明者使用加法同态加密技术在不知情的情况下对数据进行运算,生成包含答案的加密信息,作为对挑战的响应。这个方法的安全性基于「复杂性杠杆假设」,认为对于具备超常计算资源的对手,某些被认为难解的计算问题可能被解决 (Damg?rd, Fazio &Nicolosi, 2006)。 Ventre 和 Visconti 在 2009 年提出的「弱可归责可靠性」概念是对这一假设的替代,要求对手在提出虚假证明时,不仅需意识到其虚假性,还必须清楚自己如何成功制造这一伪证。这一要求显著增加了欺骗的难度,因为对手必须明确自己的欺骗手段。在实际操作中,使用此概念的对手需要提供特定证明,其中包含针对指定验证者的密文信息,无该验证者私钥难以完成证明,从而在对手试图伪造证明时,通过检测暴露其行为 (Ventre andVisconti, 2009)。 Unruh 变换是 2015 年提出的一种 Fiat-Shamir 转换的替代方案。Fiat-Shamir 方法通常在面对量子计算时并不安全,并且对于某些协议可能产生不安全的方案(Unruh, 2015)。相比之下,Unruh 变换在随机预言机模型(ROM)中,为任何交互式协议提供了对抗量子对手的可证明安全的非交互式零知识证明(NIZK)。与 Fiat-Shamir 方法相似,Unruh 变换无需额外的设置步骤(Ambainis, Rosmanis & Unruh, 2014)。 此外,Kalai 等人提出了一种基于私有信息检索技术的任意决策问题论证系统。该方法采用多证明者交互式证明系统(MIP)模型,并通过 Aiello 等人的方法,将 MIP 转换为一个论证系统 。这一构造在标准模型中运行,不需要依赖随机预言机假设。这种方法被应用于一些基于「普通人证明(Proofs-for-Muggles)」的零知识论证中 (Kalai, Raz& Rothblum, 2014)。 在这些技术基础上,非交互式零知识证明(NIZK)已被广泛应用于各种需要高度安全和隐私保护的领域,如金融交易、电子投票和区块链技术等。通过减少交互次数和优化证明生成与验证过程,NIZK 不仅提高了系统的效率,还增强了安全性和隐私保护能力。在未来,随着这些技术的进一步发展和完善,我们可以预期 NIZK 将在更多领域中发挥重要作用,为实现更加安全和高效的信息处理和传输提供坚实的技术基础(Partala, Nguyen & Pirttikangas, 2020)。 三、基于电路的零知识证明 1. 背景 在密码学领域,尤其是在处理需要高度并行化和特定类型的计算任务(如大规模矩阵运算)时,传统的图灵机模型展现出一定的局限性。图灵机模型需通过复杂的内存管理机制来模拟无限长的纸带,并且不适合直接表达并行计算和流水线操作。相比之下,电路模型以其独特的计算结构优势,更适合于某些特定的密码学处理任务 ( Chaidos, 2017)。本文将详细探讨基于电路的零知识证明系统(Zero-KnowledgeProof Systems Based on Circuit Models),这类系统特别强调使用电路(通常是算术电路或布尔电路)来表达和验证计算过程。 2. 电路模型的基本概念与特点 在基于电路的计算模型中,电路被定义为一种特殊的计算模型,它能将任何计算过程转换为一系列的门和连线,这些门执行特定的逻辑或算术操作。具体而言,电路模型主要分为两大类: 算术电路:主要由加法和乘法门组成,用于处理有限域上的元素。算术电路适用于执行复杂的数值运算,广泛应用于加密算法和数值分析中。 逻辑电路:由与门、或门、非门等基本逻辑门构成,用于处理布尔运算。逻辑电路适合于执行简单的判断逻辑和二进制计算,常用于实现各类控制系统和简单的数据处理任务 ( Chaidos, 2017)。 3. 零知识证明中的电路设计与应用 在零知识证明系统中,电路设计的过程涉及将待证明的问题表达为一个电路,这一过程需要设计 zk 电路需要大量的「逆向思维」:「如果一个计算的声称输出是真实的,则输出必须满足一定的要求。如果这些要求难以仅用加法或乘法建模,我们要求证明者进行额外工作,以便我们更容易地模型化这些要求。」设计过程通常遵循以下步骤 ( Chaidos, 2017): 问题表示:首先将待证明的问题如密码学哈希函数的计算过程,转换为电路的形式。这包括将计算步骤分解为电路中的基本单元,如门和连线。 电路优化:通过技术手段如门合并和常数折叠,优化电路设计,减少所需的门数量和计算步骤,从而提高系统的运行效率和响应速度。 转换为多项式表示:为适配零知识证明技术,将优化后的电路进一步转换为多项式形式。每个电路元件和连接都对应于特定的多项式约束。 生成公共参考字符串(CRS):在系统初始化阶段,生成包括证明密钥和验证密钥在内的公共参考字符串,以供后续的证明生成和验证过程使用。 证明生成与验证:证明者根据其私有输入和 CRS,在电路上执行计算,生成零知识证明。验证者则可以根据公开的电路描述和 CRS,验证证明的正确性,而无需了解证明者的私有信息 ( Chaidos, 2017)。 零知识证明电路设计涉及将特定的计算过程转化为电路表示,并通过构建多项式约束来确保计算结果的准确性,同时避免泄露任何额外的个人信息。在电路设计中,关键任务是优化电路的结构并生成有效的多项式表示,这是为了提升证明生成与验证的效率。通过这些步骤实施,零知识证明技术能够在不泄露额外信息的前提下,验证计算的正确性,确保了隐私保护与数据安全性的双重需求得到满足 ( Chaidos, 2017)。 4. 潜在的缺陷和挑战 弊端包括: 1.电路复杂性和规模:复杂计算需要庞大的电路,导致证明生成和验证的计算成本显著增加,尤其是在处理大规模数据时; 2.优化难度:尽管技术手段(如门合并、常数折叠等)可以优化电路,但设计和优化高效电路仍然需要深厚的专业知识; 3.特定计算任务的适应性:不同计算任务需要不同的电路设计,为每个具体任务设计高效电路可能耗时且难以推广; 4.加密算法实现难度:实现复杂的密码学算法(如哈希函数或公钥加密)可能需要大量的逻辑门,使电路设计和实现变得困难; 5.资源消耗:大规模电路需要大量硬件资源,可能在功耗、热量和物理空间等方面遇到实际硬件实现的瓶颈(Goldreich, 2004 ;Chaidos, 2017 ;Partala, Nguyen & Pirttikangas, 2020 ;Sun 等, 2021)。 解决方案和改进方向: 1.电路压缩技术:通过研究和应用高效的电路压缩技术,减少所需逻辑门数量和计算资源; 2.模块化设计:通过模块化设计电路,提高电路设计的复用性和可扩展性,减少为不同任务重新设计电路的工作量; 3.硬件加速:利用专用硬件(如 FPGA 或 ASIC)加速电路计算,提高零知识证明的整体性能(Goldreich, 2004 ;Chaidos, 2017 ;Partala, Nguyen & Pirttikangas, 2020 ;Sun 等,2021)。 四、零知识证明模型 1. 背景 基于电路的零知识证明通用性较差,需要为特定问题开发新的模型和算法,现有多种高级语言编译器和低级电路组合工具去进行电路生成和设计算法,相关计算的转换可以通过手动电路构建工具或自动编译器完成。手动转换通常能产生更优化的电路,而自动转换对开发者更方便。性能关键应用通常需要手动转换工具(Chaidos, 2017 ;Partala, Nguyen & Pirttikangas, 2020 ;Sun 等, 2021)。 本文将讨论其中最著名的几种。总的来说,这些模型都是 zkSNARKs 技术的扩展或变体,每个都试图在特定的应用需求(如证明大小、计算复杂性、设置需求等)中提供优化。 每种协议都有其特定的应用、优势和局限性,特别是在设置要求、证明大小、验证速度和计算开销方面。它们在各个领域得到应用,从加密货币隐私和安全投票系统到以零知识方式验证的一般计算等(?apko, Vukmirovi? & Nedi?, 2019)。 2. 常见算法模型 1. zkSNARK 模型: 2011 年,由密码学者 Bitansky 等人提出,作为「零知识简洁非交互式知识论证」(Zero-KnowledgeSuccinct Non-Interactive Argument of Knowledge)的缩写,它是一种改进的零知识证明机制,如果存在可提取碰撞抗性哈希(ECRH)函数,那么实现针对 NP 问题的 SNARK 是可能的,并展示了 SNARK 在计算委托、简洁非交互式零知识证明以及简洁双方安全计算等多种情境中的适用性。这项研究还表明,SNARK 的存在意味着 ECRH 的必要性,确立了这些密码学原语之间的基础性联系 (Bitanskyet al., 2011)。 zkSNARK 系统由设置、证明者和验证者三部分组成。设置过程生成证明密钥(PK)和验证密钥(VK),使用预定义的安全参数 l 和 F- 算术电路 C。该电路的所有输入和输出均为域 F 中的元素。PK 用于生成可验证的证明,而 VK 用于验证生成的证明。基于生成的 PK,证明者使用输入 x ∈ Fn 和证人 W ∈ Fh 生成证明 p,其中 C(x, W) = 0 l。这里,C(x, W) = 0 l 表示电路 C 的输出为 0 l,x 和 W 是电路 C 的输入参数。n、h 和 l 分别表示 x、W 和 C 输出的维度。最后,验证者使用 VK、x 和 p 来验证 p,根据验证结果决定接受或拒绝该证明 (Bitanskyet al., 2011)。 此外,zkSNARK 还具备一些额外特性。首先,验证过程可以在短时间内完成,并且证明的大小通常只有几个字节。其次,证明者和验证者之间不需要同步通信,任何验证者都可以离线验证证明。最后,证明者算法只能在多项式时间内实现。从那时起,已经出现了多种改进的 zkSNARK 模型,进一步优化了其性能和应用范围 (Bitanskyet al., 2011)。 2. Ben-Sasson 的模型:Ben-Sasson 等人在 2013 年和 2014 年提出了一种针对冯·诺依曼 RISC 架构程序执行的一种新的 zkSNARK 模型。然后,基于所提出的通用电路生成器,Ben-Sasson 等人建立了一个系统,并展示了其在验证程序执行中的应用。该系统包含两个组件:用于验证算术电路可满足性的密码学证明系统,以及将程序执行转换为算术电路的电路生成器。该设计在功能和效率上均优于之前的工作,尤其是电路生成器的通用性和输出电路大小的加性依赖。实验评估表明,该系统可以处理多达 10, 000 条指令的程序,并在高安全级别下生成简洁的证明,其验证时间仅为 5 毫秒。其价值在于为区块链和隐私保护智能合约等实际应用提供了高效、通用且安全的 zk-SNARKs 解决方案 (Ben-Sasson et al., 2013, 2014)。 3. Pinocchio 模型:Parno 等人(2013)提出,是一个完整的非交互零知识论证生成套件 (Parno etal., 2013)。它包含一个高级编译器,高级编译器为开发者提供了一种将计算转化为电路的简便方法。这些编译器接受用高级语言编写的代码,因此新旧算法都能轻松转换。然而,为生成合适大小的电路,代码结构可能会有一些限制。 Pinocchio 的另一个特点是使用了一种被称为二次算术程序(QuadraticArithmetic Programs,QAPs)的数学结构,可以高效地将计算任务转换为验证任务。QAPs 能够将任意算术电路编码为多项式集合,并且只需要线性时间和空间复杂度来生成这些多项式。Pinocchio 生成的证明大小为 288 字节,不随计算任务的复杂度和输入输出大小变化。这大大减少了数据传输和存储的开销。Pinocchio 的验证时间通常为 10 毫秒,相比之前的工作,验证时间减少了 5-7 个数量级。对于某些应用,Pinocchio 甚至能够实现比本地执行更快的验证速度。减少工作者的证明开销:Pinocchio 还减少了工作者生成证明的开销,相比之前的工作,减少了 19-60 倍 (Parno etal., 2013)。 4. Bulletproofs 模型: 2017 年 BenediktBünz 等人(2018)设计了新型非交互式 ZKP 模型。不需要可信设置,且证明大小随见证值大小呈对数增长。Bulletproofs 特别适用于在保密交易中的区间证明,能够通过使用最小的群和字段元素数量证明一个值在某个范围内。此外,Bulletproofs 还支持区间证明的聚合,使得可以通过一个简洁的多方计算协议生成一个单一的证明,大幅减少了通信和验证时间。Bulletproofs 的设计使其在加密货币等分布式和无需信任的环境中具有很高的效率和实用性。Bulletproofs 严格意义上并非传统的基于电路的协议,它们的简洁性不如 SNARKs,验证 Bulletproof 的时间比验证 SNARK 证明更长。但在不需要可信设置的场景中更高效。 5. Ligero 模型:Ames 等人(2017)提出的一种轻量级的零知识论证模型。Ligero 的通信复杂性与验证电路大小的平方根成正比。此外,Ligero 可以依赖任何抗碰撞的哈希函数。此外,Ligero 可以是随机预言模型中的一个 zkSNARK 方案。此模型不需要受信任的设置或公钥密码系统。Ligero 可用于非常大的验证电路。同时,它适用于应用中的中等大型电路。 3. 基于线性 PCP 和离散对数问题的方案 Ishai 和 Paskin(2007)提出利用加法同态公钥加密减少交互式线性 PCP 的通信复杂性。随后 Groth 等人在 2006 年至 2008 年发表多篇研究提出了基于离散对数问题和双线性配对的 NIZK 方案,实现了完美完备性、计算正确性和完美零知识。该方案将陈述表示为代数约束满足问题,使用类似 Pedersen 承诺的加密承诺方案实现次线性证明长度和非交互性,而无需 Fiat-Shamir 启发式。尽管需要较大的 CRS 和强加密假设「指数知识」,足够长的 CRS 可实现常量证明长度。验证和证明代价较高,建议采用「模拟可提取性」安全模型。这个类型方案基于线性 PCP 和 / 或离散对数问题,但均不具备抗量子安全性(Groth, 2006, 2006, 2008; Groth & Sahai, 2007)。 6. Groth 16 模型:是一种高效的非交互式零知识证明系统,由 Jens Groth 在 2016 年提出。该协议基于椭圆曲线配对和二次算术程序(QAP),旨在提供简洁、快速和安全的零知识证明 。 7. Sonic 模型:M. Maller 等人(2019)提出,基于 Groth 的可更新 CRS 模型,使用多项式承诺方案、配对和算术电路。需要可信设置,可通过安全多方计算实现。一旦生成 CRS,支持任意大小电路。 8. PLONK 模型: 2019 年提出的一个通用的 zk-SNARK,使用排列多项式简化算术电路表示,使证明更简单和高效;它具有多功能性,并支持递归证明组合(Gabizon, Williamson & Ciobotaru, 2019)。PLONK 模型自称减少了 Sonic 的证明长度并提高了证明效率,但尚未通过同行评审。 9. Marlin 模型:一种改进式的 zk-SNARK 协议,将代数证明系统的效率与 Sonic 和 PLONK 的通用和可更新设置属性相结合,提供了证明大小和验证时间方面的改进 (Chiesa etal., 2019)。 10. SLONK 模型:Zac 和 Ariel 在 ethresear 一个文件里介绍的新型协议,一种 PLONK 的扩展,旨在解决特定的计算效率问题并增强原始 PLONK 系统的功能,通常涉及底层加密假设或实现的变化 (Ethereum Research, 2019)。 11. SuperSonic 模型:一种应用新颖的多项式承诺方案,将 Sonic 转换为无需可信设置的零知识方案。不具备抗量子安全性 (Bünz, Fisch & Szepieniec, 2019)。 4. 基于普通人证明的方案 「普通人证明」(Proofs-for-Muggles)是由 Goldwasser、Kalai 和 Rothblum 在 2008 年提出的一种新的零知识证明方法。该方法在原始交互证明模型中为多项式时间证明者构建交互证明,适用于广泛的问题。通过 Kalai 等人的转换,这些证明可以变为非交互式零知识证明(Kalai, Raz &Rothblum, 2014)。 12. Hyrax 模型:基于普通人证明,Wahby 等人(2018)首先设计了一个低通信、低成本的零知识论证方案 Hyrax,对证明者和验证者来说成本很低。在这个方案中,这个论证中没有受信任的设置。如果应用于批量语句,则验证时间与算术电路大小具有亚线性关系,且常数很好。证明者的运行时间与算术电路大小成线性关系,常数也很好。使用 Fiat-Shamir 启发式实现非交互性,基于离散对数问题,未实现抗量子安全。 13. Libra 模型:第一个具有线性证明者时间、简洁证明大小和验证时间的 ZKP 模型。在 Libra 中,为了减少验证的开销,零知识机制通过一种可以掩盖证明者响应的轻微随机多项式的方法来实现。此外,Libra 需要一次性受信任的设置,这只依赖于电路的输入大小。Libra 具有出色的渐近性能和证明者的卓越效率。其证明大小和验证时间的性能也非常高效 (Xie etal., 2019)。 就证明者算法的计算复杂性而言,Libra 优于 Ben-Sasson 的模型、Ligero、Hyrax 和 Aurora。此外,Libra 的证明者算法的计算复杂性与电路类型无关(Partala, Nguyen & Pirttikangas, 2020)。 14. Spartan 模型:SrinathSetty(2019)提出的旨在提供高效证明而不需要受信任设置的零知识证明系统;使用 Fiat-Shamir 转换实现非交互性。它以其轻量级设计和有效处理大电路的能力而闻名。 5. 基于概率可检验证明(PCP)的零知识 Kilian(1992)构建了第一个用于 NP 的交互式零知识论证方案,实现了多对数通信。该方案使用了抗碰撞哈希函数、交互式证明系统(IP)和概率可检验证明(PCP)。证明者和验证者(作为随机算法)通过多轮通信,验证者测试证明者对陈述的知识。通常只考虑单边错误:证明者总能为真实陈述辩护,但验证者可能以低概率接受虚假陈述。2000 年,Micali 使用 Fiat-Shamir 转换将方案转化为单消息非交互式方案。以下实现可被视为采用了这种方法: 15. STARK 模型: 2018 年,ZK-STARKs(Scalable Transparent ARgument of Knowledge) 技术由 Ben-Sasson 等人在 2018 年提出,旨在解决 zk-SNARKs 处理复杂证明时的低效问题。同时,解决了在隐私数据上验证计算完整性的问题,能够在不依赖任何受信方的情况下,提供透明且后量子安全的证明。 同年,Ben-Sasson 等人创办 StarkWareIndustries,并开发了第一个基于 ZK-STARKs 的可扩展性解决方案 StarkEx。根据以太坊的官方文档,其可通过 Fiat-Shamir 范式在随机预言机模型中实现非交互性。该构造具有抗量子安全性,但其安全性依赖于关于 Reed-Solomon 码的非标准加密假设。ZK-STARKs 具有与 ZK-SNARKs 相同的特性,但包括以下优点:a) 可扩展性:验证过程更快。透明性:验证过程是公开的。较大的证明大小:需要更高的交易手续费(StarkWare Industries, 2018 , 2018) 16. Aurora 模型:Ben-Sasson 等人(2019)提出,是基于 STARK 的简洁非交互论证(SNARG)。非交互性基于 Fiat-Shamir 构造。它适用于算术电路的满足性。Aurora 的论证大小与电路大小成多对数关系。此外,Aurora 具有几个吸引人的特点。在 Aurora 中,有一个透明的设置。不存在有效的量子计算攻击,可以破解 Aurora。此外,快速对称加密被用作黑盒。Aurora 优化了证明大小。例如,如果安全参数是 128 位,则 Aurora 的证明大小最多为 250 千字节。Aurora 和 Ligero 通过优化证明大小和计算开销,使得它们非常适合在资源有限的设备上进行零知识证明。这些优化不仅提升了效率,还扩大了零知识证明技术的应用范围,使其能够在更多实际场景中得到应用。 17. Succinct Aurora 模型:Ben-Sasson 等人(2019)于同一篇论文中提出:Aurora 协议的扩展,提供了更优化的证明大小和验证过程。它保持了 Aurora 的透明设置和安全功能,同时增强了效率。 18. Fractal 模型:Chiesa 等人(2020)提出,一种预处理 SNARK,使用递归组合提高效率和可扩展性。它利用对数证明大小和验证时间,特别适用于复杂计算。 6. 基于 CPC(通用证明构造)的设置阶段进行分类 第一代(G 1)- 每个电路需要单独的受信任设置。zkSNARK,Pinocchio 和 Groth 16 第二代(G 2)- 最初为所有电路设置一次。PlonK,Sonic,Marlin,slonk 和 Libra 第三代(G 3)- 不需要受信任设置的证明系统。Bulletproofs,STARKs,Spartan,Fractal,Supersonic,Ligero,Aurora 和 SuccinctAurora(?apko, Vukmirovi? & Nedi?, 2019 ;Partala, Nguyen & Pirttikangas, 2020)。 五、零知识虚拟机的概述和发展 1. 背景 前面介绍的部分更多的是零知识证明 ZKP 在密码学中的发展,接下来我们简单介绍一下它在计算机领域的发展。 2019 年,Andreev 等人在「ZkVM:Fast, Private, Flexible Blockchain Contracts」大会上首次提出 ZK-VM 的概念,作为零知识证明系统的一种实现方式。ZK-VM 的目标是通过运行虚拟机程序来生成零知识证明,验证程序执行的正确性而不泄露输入数据。 VM,(VirtualMachine,虚拟机)是一种软件模拟的计算机系统,能够执行程序,类似于物理计算机。VM 通常用于创建独立的操作系统环境,进行软件测试和开发等。VM 或者 VM 抽象可以在大多数情况下等同理解为 CPU 抽象,它是指将计算机的处理单元(CPU)的复杂操作和架构抽象成一组简单的、可操作的指令集架构(ISA),用于简化计算机程序的设计和执行。在这种抽象中,计算机程序可以通过虚拟机(VM)来运行,这些虚拟机模拟真实 CPU 的操作行为(Henderson, 2007)。 零知识证明(ZKP)通常需要通过 CPU 抽象进行执行。设定是证明者在私有输入上运行公共程序,并希望向验证者证明程序正确执行并产生了断言的输出,而不透露计算的输入或中间状态。CPU 抽象在这种情况下非常有用,因为它允许程序在受控的虚拟环境中运行,同时生成证明(Arun, Setty& Thaler, 2024)。 示例: 证明者希望证明其拥有一个哈希值的密码,而不透露密码: 密码 → 哈希函数 → 哈希值 私有 → 公共 一般情况下,证明者应该能够运行执行哈希操作的代码,并生成允许任何人验证证明正确性的「证明」,即证明者确实拥有给定哈希值的有效前像。 生成这些 VM 抽象证明的系统通常称为「zkVMs」。这个名称其实具有误导性,因为 ZKVM 不一定提供零知识。简而言之,ZKVM 是一种专注于零知识证明的虚拟机,扩展了传统 VM 的功能,可以通用化地降低了零知识电路的开发门槛,能够即时为任意应用或计算生成证明 ( Zhang etal., 2023)。 2. 现有的 ZKVM 的分类 按照设计目标,主要分为三类: 1. 主流型 ZKVM 这些 ZKVM 利用现有的标准指令集架构(ISA)和编译器工具链,适用于广泛的应用和开发环境。 · RISCZero(2021):使用 RISC-V 指令集,具有丰富的编译器生态系统(B?gli, 2024)。 · PolygonMiden(2021):基于标准 ISA,实现简便和高效的开发(Chawla, 2021)。 · zkWASM(2022):zkWASM 实现了 WebAssembly(WASM)指令集的零知识证明,WASM 是一种广泛采用的标准指令集(DelphinusLab, 2022 )。 2. EVM 等效型 ZKVM · 这些 ZKVM 专门设计用于与以太坊虚拟机(EVM)兼容,能够直接运行以太坊的字节码。 zkEVM 项目:多个项目致力于实现与 EVM 的字节码级兼容,如 zkSync ( MatterLabs, 2020) 和 Polygon Hermez (Polygon Labs, 2021)。 3. 零知识优化(零知识友好)型 ZKVM 这些 ZKVM 优化了零知识证明的效率和性能,专为特定应用场景设计。 · Cairo-VM(2018):简单且与 SNARK 证明兼容,其指令集特别设计为算术友好,便于在零知识电路中实现基本算术运算,如加法、乘法等 (StarkWare, 2018)。 · Valida(2023):针对特定应用进行了优化,例如通过优化算法,减少了生成证明所需的计算资源和时间;轻量级设计使其适用于各种硬件和软件环境 (LitaFoundation, 2023)。 · TinyRAM(2013):不依赖标准工具链:由于其简化和优化的设计,通常不支持 LLVM 或 GCC 工具链,只能用于小规模定制软件组件 ( Ben-Sasson et al., 2013)。 当前的普遍观点是,更简单的 VM 可以转换为每步门数更少的电路。这在特别简单且显然对 SNARK 友好的 VM(如 TinyRAM 和 Cairo-VM)设计中最为明显。然而,这需要额外的开销,因为在简单 VM 上实现现实世界 CPU 的原始操作需要许多原始指令(Arun, Setty& Thaler, 2024)。 3. 前端与后端范式 从程序设计视角,ZKP 系统一般可以划分为前端 frontend 和后端 backend 两个部分。ZKP 系统的 Frontend 部分的主要使用低级别语言来表示高级别语言,例如可以将一个一般地计算问题使用较低级别的电路语言表示,如 R 1 CS 电路约束构建计算等(比如 circom 使用 R 1 CS 描述其前端电路)。ZKP 系统的 Backend 部分即密码学证明系统,主要将 frontend 构建低级别的语言描述的电路,转换为生成证明和验证正确性等,比如常用的 backend 系统协议有 Groth 16 和 Plonk 等(Arun, Setty& Thaler, 2024 ;Zhang et al., 2023)。 通常,电路将逐步「执行」计算程序的每一步(借助不受信任的「建议输入」)。执行 CPU 的一步概念上涉及两个任务:(1)识别该步骤应执行的基本指令,(2)执行指令并适当地更新 CPU 状态。现有前端通过精心设计的门或约束实现这些任务。这既耗时又容易出错,也导致电路比实际需要的大得多(Arun, Setty& Thaler, 2024 ;Zhang et al., 2023)。 4.ZKVM 范式的优缺点 优点: 1.利用现有的 ISA:例如,RISC-V 和 EVM 指令集,可以利用现有的编译器基础设施和工具链,无需从头构建基础设施。可以直接调用现有的编译器,将高层语言编写的证人检查程序转换为 ISA 的汇编代码,并受益于之前的审核或其他验证工作。 2.单一电路支持多程序:zkVM 允许一个电路运行所有程序,直到达到某个时间限制,而其他方法可能需要为每个程序重新运行前端。 3.重复结构的电路:前端输出具有重复结构的电路,针对这些电路的后端可以更快地处理(Arun, Setty& Thaler, 2024 ;Zhang et al., 2023)。 缺点: 1.通用性带来的开销:为了支持所有可能的 CPU 指令序列,zkVM 电路需要为其通用性付出代价,导致电路规模和证明成本的增加。 2.高成本操作:在 zkVM 中实现某些重要操作(如加密操作)非常昂贵。例如,ECDSA 签名验证在真实 CPU 上需要 100 微秒,在 RISC-V 指令上则需数百万条指令。因此,zkVM 项目包含手工优化的电路和查找表,用于计算特定功能。 3.证明成本高:即使对于非常简单的 ISA,现有 zkVM 的证明者成本仍然很高。例如,Cairo-VM 的证明者每步需要加密提交 51 个域元素,这意味着执行一个原始指令可能需要在真实 CPU 上执行数百万条指令,限制了其在复杂应用中的适用性(Arun, Setty& Thaler, 2024 ;Zhang et al., 2023)。 六、零知识以太坊虚拟机的概述和发展 1. 背景 ZKEVM(零知识以太坊虚拟机)和 ZKVM(零知识虚拟机)都是应用零知识证明(ZKP)技术的虚拟机。以太坊虚拟机(EVM)是以太坊区块链系统的一部分,负责处理智能合约的部署和执行。EVM 具有基于堆栈的架构,是一个计算引擎,提供特定指令集的计算和存储(如日志操作、执行、内存和存储访问、控制流、记录、调用等)。EVM 的角色是应用智能合约的操作后,更新以太坊的状态。ZKEVM 专为以太坊设计,主要用于验证智能合约执行的正确性,同时保护交易隐私。ZKEVM 将 EVM 指令集转换到 ZK 系统中执行,每条指令都需提供证明,包括状态证明和执行正确性证明(?apko, Vukmirovi? & Nedi?, 2019)。 ZKEVM 目前比较主流的方案有 STARKWARE,ZkSync,Polygen-Hermez,Scroll 等,下面是对这个几个项目的简介(?apko, Vukmirovi? & Nedi?, 2019): STARKWARE :Ben-Sasson 等人(2018)创办,致力于使用 STARK 零知识证明技术提升区块链的隐私和扩展性 zkSync:由 AlexGluchowski(2020)等人创立 Matter Labs,,提出基于 zk-rollups 的以太坊 Layer 2 扩展解决方案。 Polygon-Hermez:Hermez 原先是独立项目,于 2020 年发布。2021 年 8 月被 Polygon 收购后成为 PolygonHermez,专注于高吞吐量的 zk-rollups 解决方案。 Scroll:Zhang 和 Peng(2021)创立,实现了更高的交易吞吐量和更低的 Gas 费用,从而提高了以太坊的整体性能和用户体验。 一般按照对 EVM 的兼容级别可以划分为(?apko, Vukmirovi? & Nedi?, 2019): 1.EVM-EVM-compatibility 智能合约功能级别兼容,如 STARKWARE, zkSync 2.EVM-equivalence,EVM 指令级别兼容(等同),如 polygen-Hrmez,scroll 基于零知识的以太坊系统改进解决方案请见图 1
图 1 基于零知识的以太坊系统改进解决方案 2. ZKEVM 的工作原理 节点程序处理:节点程序处理和验证执行日志、区块头、交易、合约字节码、默克尔证明等,并将这些数据发送给 zkEVM 处理。 生成 ZK 证明:zkEVM 使用电路生成执行结果的 ZK 证明(状态和执行正确性证明),这些电路功能主要使用 table 和特制 circuit 来实现。 聚合证明:使用聚合电路将大的证明生成更小的证明,如使用递归证明。 发送到 L1 合约:聚合证明以交易形式发送给 L1 合约执行(?apko, Vukmirovi? & Nedi?, 2019)。 3. ZKEVM 的实现流程 获取数据:从以太坊区块链系统获取数据,包括交易、区块头、合约等。 处理数据:处理和验证执行日志、区块头、交易、合约字节码、默克尔证明等。 生成证明:使用电路生成 ZK 证明,确保每条指令的状态更新和执行正确性。 递归证明:将生成的大证明压缩为更小的聚合证明。 提交证明:将聚合证明提交给 L1 合约,以完成交易验证(?apko, Vukmirovi? & Nedi?, 2019)。 4. ZKEVM 的特点 提升交易处理能力:通过 L2 上的 ZKEVM 执行交易,减少 L1 的负载。 隐私保护:在验证智能合约执行的同时保护交易隐私。 高效验证:使用零知识证明技术,实现高效的状态和执行正确性验证(?apko, Vukmirovi? & Nedi?, 2019)。 七、零知识二层网络方案概述与发展 1. 背景 以太坊区块链是当前最广泛采用的区块链生态系统之一。然而,以太坊面临严重的扩展性问题,导致使用成本高昂。零知识二层网络方案(ZK Rollup)基于零知识证明(ZKP),是一种针对以太坊扩容的二层网络(Layer 2)解决方案,克服了 OptimisticRollups 交易最终确认时间过长的缺陷 ( Ganguly, 2023)。 2.ZK Rollup 的工作机制 ZK Rollup 允许在一笔交易内实现可扩展性。L1 上的智能合约负责处理并验证所有转账,理想情况下只生成一笔交易。这是通过在链下执行交易来减少以太坊上的计算资源使用,并将最终的签名交易重新放回链上进行。这一步骤被称为有效性证明(ValidityProof)。在某些情况下,可能无法在单一证明内完成验证,需要额外的交易将 rollup 上的数据发布到以太坊主链上,以确保数据的可用性 ( Ganguly, 2023)。 在空间方面,使用 ZK Rollup 由于不需要像普通智能合约那样存储数据,因此提高了效率。每笔交易仅需要验证证明,这进一步确认了数据的最小化,使得它们更便宜和更快 ( Ganguly, 2023)。 尽管 ZK Rollup 名称中包含「ZK」(零知识)的术语,但它们主要利用零知识证明的简洁性来提高区块链交易的处理效率,而不是主要关注隐私保护 ( Ganguly, 2023)。 3. ZKRollup 的缺点与优化 ZK Rollup(零知识汇总)作为以太坊扩展性的 Layer 2 解决方案,虽然在提高交易处理效率方面表现优异,但其主要问题在于计算成本非常高。然而,通过一些优化方案,可以显著提高 ZK Rollup 的性能和可行性 ((?apko, Vukmirovi? & Nedi?, 2019)。 1. 优化密码算法的计算 优化密码算法的计算过程可以提高 ZK Rollup 的效率,减少计算时间和资源消耗。例如,Plonky 2 由 PolygonZero(前身为 MIR)提出,是一种去中心化的 ZK Rollup 解决方案。Plonky 2 是一种递归 SNARK,比其他以太坊兼容替代品快 100 倍,结合了 STARKs 和 SNARKs 的最佳特性: Plonk 和 FRI:提供快速证明且无需信任设置。 支持递归:通过递归证明提高效率。 低验证成本:通过 64 位递归 FRI 与 Plonk 结合,实现高效证明。 2. 混合 Optimistic 和 ZK Rollup 例如,PolygonNightfall 是一种混合 Rollup,结合了 Optimistic 和 ZK Rollup 的特点,旨在增加交易隐私并减少转账费用(最多可减少 86% )。 3. 开发专用 ZK EVM 专用 ZK EVM 是为提高 ZK Rollup 算法而设计的,可以优化零知识证明过程。以下是几种具体方案: AppliedZKP:由以太坊基金会资助的开源项目,实现了以太坊 EVM 原生操作码的 ZK,使用了 halo 2、KZG 和 Barreto-Naehrig(BN-254)椭圆曲线配对等密码算法。 zkSync:由 Matter Labs 开发的 zkEVM,是一个自定义 EVM,实现了将合约代码编译成 YUL(Solidity 编译器的中间语言),然后再编译成支持的自定义字节码,使用 Plonk 的扩展版 ultraPlonk。 Polygon Hermez:自定义 EVM 兼容的去中心化 Rollup,将合约代码编译成支持的微指令集,使用 Plonk、KZG 和 Groth 16 证明系统。 Sin 7 Y zkEVM:实现了 EVM 原生操作码的 ZK,并优化了专用操作码,使用 halo 2、KZG 和 RecursivePlonk。 Polygon Miden:基于 STARK 的通用零知识虚拟机。 4. 硬件优化 硬件优化可以显著提升 ZK Rollup 的性能。以下是几种硬件优化方案: DIZK(DIstributedZero Knowledge):通过在计算集群上分布执行 zkSNARK 证明来进行优化。硬件架构包括两个子系统,一个用于多项式计算(POLY),具有大尺寸数论变换(NTTs),另一个用于执行椭圆曲线(ECs)上的多标量乘法(MSM)。PipeMSM 是用于在 FPGA 上实现的流水线设计 MSM 算法。 基于 FPGA 的 ZKP 硬件加速器设计:包括多个 FFT(快速傅里叶变换)单元和 FFT 操作的分解,多个 MAC(乘加电路)单元,以及多个 ECP(椭圆曲线处理)单元,以减少计算开销。基于 FPGA 的 zk-SNARK 设计减少了证明时间约 10 倍。 Bulletproof 协议的硬件加速:通过 CPU-GPU 协作框架和 GPU 上的并行 Bulletproofs 实现(?apko, Vukmirovi? & Nedi?, 2019)。 八、零知识证明的未来发展方向 1. 加速计算环境的发展 零知识证明协议(如 ZKSNARKs 和 ZKSTARKs)在执行过程中通常涉及大量复杂的数学运算,这些运算需要在极短的时间内完成,对计算资源(如 CPU 和 GPU)提出了极高的要求,导致计算复杂性高、计算时间长。此外,生成和验证零知识证明需要频繁访问大容量数据,对内存带宽提出了高要求。现代计算机系统的内存带宽有限,无法高效支持如此高频的数据访问需求,导致性能瓶颈。最终,高计算负载导致高能耗,尤其是在区块链和去中心化应用中,需要持续进行大量证明计算时。因此,尽管软件优化方案可以部分缓解这些问题,但由于通用计算硬件的物理限制,难以达到硬件加速的高效率和低能耗水平。混合解决方案在保持灵活性的同时,可以实现较高的性能提升 (Zhang etal., 2021)。 ZK-ASIC(专用集成电路) 2020 年期间多个项目出现,旨在通过硬件如 GPU 或者 FPGA 加速优化零知识证明(ZKP)的生成和验证过程,提高效率 (Filecoin, 2024; Coda, 2024;Gpu groth 16 prover, 2024; Roy et al., 2019; Devlin, 2024 ;Javeed& Wang, 2017)。 2021 年:Zhang 等人提出了一种基于流水线架构的零知识证明加速方案,利用 Pippenger 算法优化多标量乘法(MSM),通过「解卷」快速傅里叶变换(FFT)减少数据传输延迟 (Zhang etal., 2021)。 ZKCoprocessor(协处理器) Axiom(2022)提出 ZKCoprocessor 概念,即 ZK 协处理器。协处理器是指增强 CPU 并提供浮点运算、加密运算或图形处理等专门操作的单独芯片。尽管随着 CPU 变得越来越强大,该术语已不再常用,但 GPU 仍可视为 CPU 的一种协处理器,尤其是在机器学习背景下。 ZK 协处理器这一术语将物理协处理器芯片的类比扩展到区块链计算,允许智能合约开发人员无状态地证明现有链上数据的链下计算。智能合约开发者面临的最大瓶颈之一仍然是链上计算的高昂成本。由于每项操作都要计算 gas,因此复杂应用逻辑的成本很快就会变得不可行。ZK 协处理器为链上应用引入了一种新的设计模式,消除了必须在区块链虚拟机中完成计算的限制。这使应用程序能够访问更多数据并以比以前更大的规模运行(Axiom, 2022)。 2. ZKML 的提出和发展 ZKML 的概念 零知识机器学习(Zero-KnowledgeMachine Learning, ZKML)是将零知识证明(ZKP)技术应用于机器学习中的一个新兴领域。ZKML 的核心思想是允许在不泄露数据或模型细节的情况下验证机器学习计算结果。这不仅可以保护数据隐私,还能确保计算结果的可信性和正确性 ( Zhang etal., 2020 )。 ZKML 的发展 2020 年,张学者等人在 2020 年的 CCS 会议上首次系统地提出了 ZKML 的概念,展示了如何在不泄露数据或模型细节的情况下进行决策树预测的零知识证明。这为 ZKML 奠定了理论基础。 2022 年,Wang 和 Hoang 进一步研究并实现了 ZKML,并提出了一种高效的零知识机器学习推理管道,展示了如何在现实应用中实现 ZKML。研究表明,尽管 ZKP 技术复杂,但通过合理的优化,可以在保证数据隐私和计算正确性的同时,达到可接受的计算性能。 3.ZKP 扩容技术相关发展 ZKThreads 的概念提出 2021 年,StarkWare 提出了 ZKThreads 的概念,旨在结合零知识证明(ZKP)和分片技术,为去中心化应用(DApps)提供可扩展性和定制性,而不会产生碎片化问题。ZKThreads 通过在基础层直接回退,确保每一步的实时性,从而提高了安全性和可组合性。 ZKThreads 的主要在单链结构,rollup 流动性问题,和 Proto-Danksharding 三个方面进行了优化。 单链解决方案:在传统的单链架构中,所有交易都在一条链上进行处理,导致系统负载过重,扩展性差。ZKThreads 通过将数据和计算任务分配到多个分片中,显著提升了处理效率。 ZK-rollups 解决方案:虽然 ZK-rollups 已经显著提高了交易处理速度和降低了成本,但它们通常是独立运行的,导致流动性碎片化和互操作性问题。ZKThreads 提供了一个标准化的开发环境,支持不同分片之间的互操作性,解决了流动性碎片化的问题。 Proto-Danksharding 技术:这是以太坊的一种内部改进方案,通过暂存数据块来降低 zk-rollups 的交易成本。ZKThreads 在此基础上进一步改进,通过更高效的分片架构,减少了对临时数据存储的依赖,提高了系统的整体效率和安全性(StarkWare, 2021)。 ZK Sharding 的概念提出 此后,在 2022 年,NilFoundation 提出了 ZK Sharding 的概念,旨在通过结合零知识证明(ZKP)和分片技术,来实现以太坊的扩展性和更快的交易速度。这一技术旨在将以太坊网络分成多个部分,以更便宜和更高效的方式处理交易。该技术包括 zkSharding,利用零知识技术生成证明,确保跨不同分片的交易在提交到主链之前是有效的。这种方法不仅提升了交易速度,还减少了链上数据的碎片化问题,确保了经济安全性和流动性。 4. ZKP 互操作性的发展 ZK State Channels 2021 年,ZK StateChannels 的概念由 Virtual Labs 提出,结合了零知识证明(ZKP)和状态通道技术,旨在通过状态通道实现高效的链外交易,同时利用零知识证明来确保交易的隐私和安全。 ZK State Channels 替代的原有方案 1. 传统状态通道(StateChannels): 原有方案:传统状态通道允许两个用户通过锁定资金在智能合约中进行点对点(P2P)交易。由于资金已被锁定,用户之间的签名交换可以直接进行,不涉及任何 gas 费用和延迟。然而,这种方法需要预定义的地址,且通道的开闭需要链上操作,限制了其灵活性。 替代方案:ZK StateChannels 提供了无限参与者的支持,允许动态进入和退出,不需要预定义用户地址。此外,通过零知识证明,ZK StateChannels 提供了即时的跨链访问和自验证的证明,解决了传统状态通道的灵活性和扩展性问题。 2. 多链支持: 原有方案:传统状态通道通常仅支持单一链上的交易,无法实现跨链操作,限制了用户的操作范围。 替代方案:ZK StateChannels 通过零知识证明技术,实现了跨链的即时交易和资产流动,无需中间桥接,极大地提升了多链互操作性。 3. 预定义地址限制: 原有方案:在传统状态通道中,交易参与者的地址必须在通道创建时预定义,如果有新的参与者加入或离开,通道必须关闭并重新打开,这增加了操作复杂性和费用。 替代方案:ZK StateChannels 允许动态加入和退出,新的参与者可以随时加入现有通道,而不影响当前用户的操作,极大地提高了系统的灵活性和用户体验。 4.ZK Omnichain InteroperabilityProtocol 2022 年,ZKOmnichain Interoperability Protocol 由 Way Network 提出,旨在实现基于零知识证明的跨链资产和数据互操作性。该协议通过使用 zkRelayer、ZK Verifier、IPFS、Sender 和 Receiver 实现全链通信和数据传输。 Omnichain 项目专注于跨链互操作性,旨在提供一个低延迟、安全的网络,连接不同的区块链。它通过引入标准化的跨链交易协议,使得各区块链之间的资产和数据可以无缝转移。这种方法不仅提高了交易的效率,还确保了跨链操作的安全性。 Way Network 可以看作是 Omnichain 概念的一种具体实现,特别是在使用零知识证明技术来增强隐私性和安全性方面。Way Network 的技术架构使得它能够在保持去中心化和高效性的同时,实现链间的无缝互操作。 总结来说,Omnichain 提供了跨链互操作性的总体框架,而 Way Network 则通过零知识证明技术,为这一框架提供了更强的隐私保护和安全性。 九、结论 本文对零知识证明(ZKP)技术及其在区块链领域的最新发展和应用进行了全面的文献综述。我们系统地审查了区块链环境中的 ZKP,调查了适用于区块链和可验证计算的最先进的零知识论证方案,并探讨了它们在匿名和保密交易以及隐私智能合约中的应用。本文列举了这些经过学术同行评审的方案和方法的优缺点,提供了这些方案的实际评估和比较的参考资料,强调了开发人员在选择特定用例的合适方案时需要具备的技能和知识。 此外,本文还展望了零知识证明在硬件加速、区块链扩展性、互操作性和隐私保护等方面的未来发展方向。通过对这些最新技术和发展趋势的详细分析,本文为理解和应用零知识证明技术提供了全面的视角,展示了其在提升区块链系统效率和安全性方面的巨大潜力。同时,这项研究为后续关于 ZK 项目投资的研究奠定了坚实的基础。 参考文献 · Ames, S., Hazay, C., Ishai, Y. and Venkitasubramaniam, M. (2017) 'Ligero', Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pp. 2087-2104. DOI: https://doi.org/10.1145/3133956.3134104. · AdaPulse (2024) 'The Convergence of Zero-Knowledge Proofs and Decentralized Systems: Part 1', AdaPulse. Available at: https://adapulse.io/the-convergence-of-zero-knowledge-proofs-and-decentralized-systems-part-1 (Accessed: 30 June 2024). · Ambainis, A., Rosmanis, A. and Unruh, D. (2014) 'Quantum attacks on classical proof systems: The hardness of quantum rewinding', in Proceedings of the IEEE 55th Annual Symposium on Foundations of Computer Science (FOCS 2014), pp. 474-483. · Andreev, O., et al. (2019) 'ZkVM: Fast, Private, Flexible Blockchain Contracts'. Available at: https://cathieyun.github.io/presentations/zkvm.html (Accessed: 30 June 2024). · Arun, A., Setty, S. and Thaler, J. (2024) 'Jolt: SNARKs for Virtual Machines via Lookups', in Joye, M. and Leander, G. (eds) Advances in Cryptology – EUROCRYPT 2024, Lecture Notes in Computer Science, vol. 14656. Cham: Springer. Available at: https://doi.org/10.1007/978-3-031-58751-1_1 (Accessed: 30 June 2024). · Axiom (2022) 'What is a ZK Coprocessor?'. Available at: https://blog.axiom.xyz (Accessed: 30 June 2024). · B?gli, R. (2024) 'Assessing RISC Zero using ZKit: An Extensible Testing and Benchmarking Suite for ZKP Frameworks'. Masters thesis, OST Ostschweizer Fachhochschule. · Burger, E. (2022) 'Decentralized Speed: Advances in Zero Knowledge Proofs', a16z. Available at: https://a16z.com/decentralized-speed-advances-in-zero-knowledge-proofs/ (Accessed: 30 June 2024). · Blum, M., Feldman, P. and Micali, S. (1988) 'Non-interactive zero-knowledge and its applications', Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing (STOC '88), pp. 103-112. DOI: https://doi.org/10.1145/62212.62222. · Bootle, J., Cerulli, A., Chaidos, P., Groth, J. and Petit, C. (2015) 'Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting', EUROCRYPT 2016: Advances in Cryptology, Lecture Notes in Computer Science, vol. 9666, pp. 327-357. Available at: https://link.springer.com/chapter/10.1007/978-3-662-49896-5_12 (Accessed: 30 June 2024). · Bayer, S. and Groth, J. (2012) 'Efficient zero-knowledge argument for correctness of a shuffle', EUROCRYPT 2012: Advances in Cryptology, Lecture Notes in Computer Science, vol. 7237, pp. 263-280. Available at: https://link.springer.com/chapter/10.1007/978-3-642-29011-4_16 (Accessed: 30 June 2024). · Bitansky, N., Canetti, R., Chiesa, A. and Tromer, E. (2011) 'From Extractable Collision Resistance to Succinct Non-Interactive Arguments of Knowledge, and Back Again',Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2011/443.pdf (Accessed: 30 June 2024). · Bünz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P. and Maxwell, G. (2018) 'Bulletproofs: Short Proofs for Confidential Transactions and More', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2017/1066.pdf (Accessed: 30 June 2024). · Bünz, B., Fisch, B. and Szepieniec, A. (2019) 'Transparent SNARKs from DARK Compilers', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2019/1229 (Accessed: 28 June 2024). · Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E. and Virza, M. (2013) 'SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge (extended version)', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2013/507.pdf (Accessed: 30 June 2024). · Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E. and Virza, M. (2014) 'Succinct Noninteractive Zero Knowledge for a Von Neumann Architecture', in Proceedings of the 23rd USENIX Security Symposium, pp. 781-796. · Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E. and Virza, M. (2014) 'Zerocash: Decentralized Anonymous Payments from Bitcoin', in Proceedings of the 2014 IEEE Symposium on Security and Privacy. · Ben-Sasson, E., Bentov, I., Horesh, Y. and Riabzev, M. (2018) 'Scalable, Transparent, and Post-Quantum Secure Computational Integrity', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2018/046.pdf (Accessed: 30 June 2024). · Ben-Sasson, E., Chiesa, A., Riabzev, M., Spooner, N., Virza, M. and Ward, N. (2019) 'Aurora: Transparent Succinct Arguments for R1CS', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2018/828.pdf (Accessed: 3 May 2024). · Chaidos, P.I.P. (2017) Zero Knowledge Protocols and Applications. Doctor of Philosophy Dissertation. University College London, Security & Crime Science. · Chawla, V. (2021) 'Polygon Unveils ZK-Rollup Solution Miden to Scale Ethereum', Crypto Briefing. Available at: https://cryptobriefing.com/polygon-unveils-miden (Accessed: 30 June 2024). · Chiesa, A., Hu, Y., Maller, M., Mishra, P., Vesely, P. and Ward, N. (2019) 'M: Preprocessing zkSNARKs with Universal and Updatable SRS'. [online] Available at: https://eprint.iacr.org/2019/1047.pdf (Accessed: 30 June 2024). · Coda Protocol (n.d.) 'Gpu groth16 prover'. Available at: https://github.com/CodaProtocol/gpu-groth16-prover-3x (Accessed: 30 June 2024). · Chiesa, A., Ojha, D. and Spooner, N. (2020) 'FRACTAL: Post-Quantum and Transparent Recursive Proofs from Holography'. [online] Available at: https://eprint.iacr.org/2019/1076.pdf (Accessed: 3 May 2024). · ?apko, D., Vukmirovi?, S. and Nedi?, N. (2019) 'State of the Art of Zero-Knowledge Proofs in Blockchain', Faculty of Technical Sciences, University of Novi Sad, Novi Sad, Serbia. Available at: [email protected], [email protected], [email protected] (Accessed: 30 June 2024). · Cramer, R. and Shoup, V. (1998) 'A practical public-key encryption scheme secure against adaptive chosen ciphertext attack', in Advances in Cryptology – CRYPTO』98, pp. 13-25. Springer. · Cramer, R. and Shoup, V. (2002) 'Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption', in Advances in Cryptology – EUROCRYPT 2002, pp. 45-64. Springer. · Canetti, R., Goldreich, O. and Halevi, S. (2003) 'On the random-oracle methodology as applied to length-restricted signature schemes'. [online] Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2003/150 (Accessed: 28 Jun. 2024). · Devlin, B.S. (n.d.) 'Fpga snark prover targeting the bn128 curve'. Available at: https://github.com/bsdevlin/fpga_snark_prover (Accessed: 30 June 2024). · Damg?rd, I., Fazio, N. and Nicolosi, A. (2006) 'Non-Interactive Zero-Knowledge from Homomorphic Encryption', in Theory of Cryptography Conference (TCC 2006), Lecture Notes in Computer Science, vol. 3876, pp. 41-59. Available at: https://iacr.org/archive/tcc2006/38760041/38760041.pdf (Accessed: 28 Jun. 2024). · Ethereum Research (2019) 'SLONK—a simple universal SNARK'. [online] Available at: https://ethresear.ch/t/slonk-a-simple-universal-snark/6420 (Accessed: 28 Jun. 2024). · Filecoin Project (n.d.) 'bellperson: Gpu parallel acceleration for zk-snark'. Available at: https://github.com/filecoin-project/bellperson (Accessed: 30 June 2024). · Fiat, A. and Shamir, A. (1986) 'How To Prove Yourself: Practical Solutions to Identification and Signature Problems', in Advances in Cryptology—CRYPTO』 86, pp. 186–194. DOI: https://doi.org/10.1007/3-540-47721-7_12. · Feige, U., Fiat, A. and Shamir, A. (1986) 'Zero-Knowledge Proofs of Identity', in Proceedings of the 19th Annual ACM Symposium on Theory of Computing (STOC 1986), pp. 210-217. DOI: 10.1145/12130.12146. · Ganguly, P. (2023) Zero-Knowledge Proofs Origination and Early Twenty-First Century Use Cases. Master of Science (Computer Science) thesis, New York University, Tandon School of Engineering. UMI Dissertation Publishing, ProQuest CSA, 789 E. Eisenhower Parkway, P.O. Box 1346, Ann Arbor, MI 48106-134. · Goldreich, O. (2004) 'Zero-Knowledge Twenty Years After Its Invention', Electronic Colloquium on Computational Complexity (ECCC), Report No. 63. Available at:https://eccc.weizmann.ac.il/report/2004/063/ (Accessed: 30 June 2024). · Goldwasser, S., Micali, S. and Rackoff, C. (1985) 'The knowledge complexity of interactive proof-systems', Proceedings of the seventeenth annual ACM symposium on Theory of computing - STOC 』85. DOI: https://doi.org/10.1145/22145.22178. · Groth, J. and Sahai, A. (2005) 'Perfect Non-Interactive Zero Knowledge for NP'. [online] Available at: https://eprint.iacr.org/2005/290.pdf (Accessed: 27 June 2024). · Groth, J. (2006) 'Simulation-sound NIZK proofs for a practical language and constant size group signatures', ASIACRYPT 2006: Advances in Cryptology, Lecture Notes in Computer Science, vol. 4284, pp. 444-459. Available at: https://link.springer.com/chapter/10.1007/11935230_29 (Accessed: 30 June 2024). · Groth, J., Ostrovsky, R. and Sahai, A. (2006) 'Fully concurrent non-malleable zero-knowledge', EUROCRYPT 2006: Advances in Cryptology, Lecture Notes in Computer Science, vol. 4004, pp. 214-235. Available at: https://link.springer.com/chapter/10.1007/11761679_14 (Accessed: 30 June 2024). · Groth, J. and Sahai, A. (2007) 'Efficient non-interactive proof systems for bilinear groups', SIAM Journal on Computing, vol. 41, no. 5, pp. 1193-1232. Available at: https://epubs.siam.org/doi/10.1137/080725386 (Accessed: 30 June 2024). · Groth, J. (2008) 'Sub-linear zero-knowledge arguments for linear algebra', CRYPTO 2008: Advances in Cryptology, Lecture Notes in Computer Science, vol. 5157, pp. 192-206. Available at: https://link.springer.com/chapter/10.1007/978-3-540-85174-5_11 (Accessed: 30 June 2024). · Groth, J. (2011) 'Minimizing Non-interactive Zero-Knowledge Proofs Using Fully Homomorphic Encryption', Journal of Cryptology, 24(4), pp. 591-623. · Groth, J., Ostrovsky, R. and Sahai, A. (2012) 'New techniques for non-interactive zero-knowledge', Journal of the ACM, 59(3), pp. 1-35. Available at: https://dl.acm.org/doi/10.1145/2220357.2220361 (Accessed: 30 June 2024). · Groth, J. (2016) 'On the Size of Pairing-based Non-interactive Arguments'. [online] DOI: https://doi.org/10.1007/978-3-662-49896-5. ·Groth, J., Kohlweiss, M. and Pintore, F. (2016) 'One-time simulation-sound QA-NIZK arguments and applications to ring signatures', ASIACRYPT 2016: Advances in Cryptology, Lecture Notes in Computer Science, vol. 10031, pp. 102-132. Available at: https://link.springer.com/chapter/10.1007/978-3-662-53887-6_4 (Accessed: 30 June 2024). · Groth, J. and Maller, M. (2017) 'Snarky signatures: Minimal signatures of knowledge from simulation-extractable SNARKs', CRYPTO 2017: Advances in Cryptology, Lecture Notes in Computer Science, vol. 10402, pp. 581-612. Available at: https://link.springer.com/chapter/10.1007/978-3-319-63715-0_20 (Accessed: 30 June 2024). · Gabizon, A., Williamson, Z.J. and Ciobotaru, O. (2019) 'PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2019/953 (Accessed: 30 June 2024). · Goldwasser, S., Kalai, Y. and Rothblum, G. (2008) 'Delegating Computation: Interactive Proofs for Muggles'. [online] Available at: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/2008-DelegatingComputation.pdf (Accessed: 30 June 2024). · Henderson, F. (2007) 'Introduction to Virtual Machines', Proceedings of the Linux Symposium. Available at: https://www.kernel.org/doc/ols/2007/ols2007v1-pages-1-10.pdf (Accessed: 30 June 2024). · Ingonyama (2023) 'Hardware Review: GPUs, FPGAs and Zero Knowledge Proofs', Ingonyama. Published on: May 4, 2023. Available at: https://www.ingonyama.com/blog/hardware-review-gpus-fpgas-and-zero-knowledge-proofs (Accessed: 30 June 2024). · Ishai, Y. and Paskin, A. (n.d.) 'Evaluating Branching Programs on Encrypted Data', Theory of Cryptography, pp. 575–594. DOI: https://doi.org/10.1007/978-3-540-70936-7_31. · Kalai, Y.T., Raz, R. and Rothblum, R.D. (2014) 'How to delegate computations: The power of no-signaling proofs', Proceedings of the Annual ACM Symposium on Theory of Computing, New York, NY, USA, pp. 485-494. · Javeed, K. and Wang, X. (2017) 'Low latency flexible FPGA implementation of point multiplication on elliptic curves over GF(p)', International Journal of Circuit Theory and Applications, 45(2), pp. 214-228. DOI: 10.1002/cta.2359. · Kilian, J. (1992) 'A note on efficient zero-knowledge proofs and arguments (extended abstract)', Proceedings of the 24th Annual ACM Symposium on Theory of Computing, pp. 723-732. · Konstantopoulos, G. (2022) 'Hardware Acceleration for Zero Knowledge Proofs', Paradigm. Available at: https://www.paradigm.xyz/2022/04/zk-hardware (Accessed: 30 June 2024). · Lita Foundation (2023) 'Announcing Lita's Valida C Compiler & zkVM'. Available at: https://www.lita.foundation (Accessed: 30 June 2024). · Lavery, S. (2024) 'Compact and Secure Zero-Knowledge Proofs for Quantum-Resistant Cryptography from Modular Lattice Innovations', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2024/652 (Accessed: 30 June 2024). · Maller, M., Bowe, S., Kohlweiss, M. and Meiklejohn, S. (2019) 'Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updateable Structured Reference Strings', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2019/099 (Accessed: 28 June 2024). · Matter Labs (2020) 'Introducing zkSync: The missing link to the mass adoption of Ethereum',Matter Labs Blog. Available at: https://blog.matter-labs.io/introducing-zksync-the-missing-link-to-the-mass-adoption-of-ethereum (Accessed: 30 June 2024). · =nil; Foundation (2023) 'zkSharding for Ethereum'. Available at: https://nil.foundation/zksharding (Accessed: 30 June 2024). · Partala, J., Nguyen, T.H. and Pirttikangas, S. (2020) 'Non-Interactive Zero-Knowledge for Blockchain: A Survey', IEEE Access. Received November 27, 2020, accepted December 13, 2020, published December 21, 2020, current version December 31, 2020. DOI: 10.1109/ACCESS.2020.3046025. · Parno, B., Howell, J., Gentry, C. and Raykova, M. (2013) 'Pinocchio: Nearly practical verifiable computation', Security and Privacy – S&P 2013, pp. 238-252. IEEE. · Polygon Labs (2021) 'Deep Dive on Polygon Hermez: Bringing Scalability to Ethereum Using zk-Technology'. Available at: https://polygon.technology/blog/polygon-unveils-miden (Accessed: 30 June 2024). · Polygon Technology (2021) 'Polygon Miden: A STARK-Based zk-Rollup'. Polygon Community Forum. Available at: https://forum.polygon.technology/t/polygon-miden-deep-dive-a-stark-based-zk-rollup/299 (Accessed: 30 June 2024). · Roy, S.S., Turan, F., Jarvinen, K., Vercauteren, F. and Verbauwhede, I. (2019) 'FPGA-based high-performance parallel architecture for homomorphic computing on encrypted data', 2019 IEEE International Symposium on High Performance Computer Architecture (HPCA), pp. 387-398. DOI: 10.1109/HPCA.2019.00051. · RISC Zero (2021) 'zkVM Overview', RISC Zero Developer Docs. Available at: https://dev.risczero.com/api/zkvm (Accessed: 30 June 2024). · Setty, S. (2019) 'Spartan: Efficient and general-purpose zkSNARKs without trusted setup',Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2019/550 (Accessed: 30 June 2024). · Sun, X., Yu, F.R., Zhang, P., Sun, Z., Xie, W. and Peng, X. (2021) 'A Survey on Zero-Knowledge Proof in Blockchain', IEEE Network, 35(4), pp. 198-205. DOI: 10.1109/ACCESS.2020.3046025. · StarkWare Industries (2018) 'StarkEx Documentation'. Available at: https://docs.starkware.co/starkex/index.html (Accessed: 30 June 2024). · StarkWare Industries (2018) 'About Us'. Available at: https://starkware.co (Accessed: 30 June 2024). · StarkWare (2018) 'Cairo Programming Language'. Available at: https://www.cairo-lang.org (Accessed: 30 June 2024). · StarkWare (2021) 'ZKThreads: A canonical ZK sharding framework for dApps'. Available at: https://starkware.co/zkthreads (Accessed: 30 June 2024). · Unruh, D. (2015) 'Non-interactive zero-knowledge proofs in the quantum random oracle model', in Oswald, E. and Fischlin, M. (eds) Advances in Cryptology. Berlin, Germany: Springer, pp. 755-784. · Ventre, C. and Visconti, I. (2009) 'Co-sound Zero-Knowledge with Public Keys', Lecture Notes in Computer Science, pp. 287–304. DOI: https://doi.org/10.1007/978-3-642-02384-2_18. · Virtual Labs (2021) 'ZK State Channel vs. State Channel'. Available at: https://docs.virtual.tech (Accessed: 30 June 2024). · Way Network (2022) 'ZK Omnichain Interoperability Protocol'. Available at: https://way.network (Accessed: 30 June 2024). · Wang, H. and Hoang, T. (2022) 'ezDPS: An Efficient and Zero-Knowledge Machine Learning Inference Pipeline', arXiv.org. DOI: https://doi.org/10.48550/arXiv.2212.05428. · Wahby, R.S., Tzialla, I., shelat, a., Thaler, J. and Walfish, M. (2018) 'Doubly-efficient zkSNARKs without trusted setup', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2017/1132.pdf (Accessed: 28 June 2024). · Xie, T., Zhang, J., Zhang, Y., Papamanthou, C. and Song, D. (2019) 'Libra: Succinct Zero-Knowledge Proofs with Optimal Prover Computation', Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2019/317 (Accessed: 28 June 2024). · Zhou, Y., Wei, Z., Ma, S. and Tang, H. (2022) 'Overview of Zero-Knowledge Proof and Its Applications in Blockchain', in Sun, Y., Cai, L., Wang, W., Song, X. and Lu, Z. (eds) Blockchain Technology and Application. CBCC 2022. Communications in Computer and Information Science, vol. 1736. Singapore: Springer. Available at: https://doi.org/10.1007/978-981-19-8877-6_5 (Accessed: 30 June 2024). · Zhang, B., Lu, G., Qiu, P., Gui, X. and Shi, Y. (2023) 'Advancing Federated Learning through Verifiable Computations and Homomorphic Encryption', Entropy, 25(11), p. 1550. Available at: https://doi.org/10.3390/e25111550(Submission received: 11 September 2023 / Revised: 1 November 2023 / Accepted: 4 November 2023 / Published: 16 November 2023). · Zhang, Y., Wang, S., Zhang, X., Dong, J., Mao, X., Long, F., Wang, C., Zhou, D., Gao, M. and Sun, G. (2021) 'PipeZK: Accelerating Zero-Knowledge Proof with a Pipelined Architecture', IEEE Xplore. DOI: https://doi.org/10.1109/ISCA52012.2021.00040. · Zhang, J., Fang, Z., Zhang, Y. and Song, D. (2020) 'Zero Knowledge Proofs for Decision Tree Predictions and Accuracy', Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. DOI: https://doi.org/10.1145/3372297.3417278. 原文链接 |
 玩币族移动版
玩币族移动版