玩币族移动版

　　编者认为比特币最为迷人地方就是它的加密学设计，中本聪完美的使用了多种加密学方法构造了整个比特币模型。比如，SHA256对block头部信息的签名、ECDSA算法产生比特币公钥和私钥、Merkle树在block中的应用、ProofOfWork中的SHA256碰撞等等。

　　编者今天要和读者分享的是一种比特币私钥共享的模型。

　　引子

　　在电影中，我们经常会看到这样的场景，一份绝密的文件需要由7个人来保存。如果把这份文件复印七份交给每个人，那么如果7个人中有一人泄密，则整个绝密文件就会被暴露。如果把文件平均分成七份，每个人手里只拿七分之一，那么如果有一人出问题，那么也无法恢复整个文件。

　　我们既不想让完整的文件在每个人手中，又不愿意在某个人出问题时，无法还原整个文件。那么，在这个时候我们就需要一个方案，让这7个人中的大多数人在场时就能恢复文件。比如，如何让7个人中的任意4个人在场，就能恢复整个文件内容，而7人中的任意3人在场都不能还原文件。

　　比特币私钥共享

　　有5个创业者 A,B,C,D,E 组成了一个关于比特币的公司，他们有一个共同的比特币地址来记录公司所得到的比特币数量，如果这时候把该地址的私钥交给每个人，那么如果其中一个人跟其他人闹翻了，就有能力把地址上的比特币转走。如果，我们把私钥平均分为5份给每个人，那么如果其中一人忘记了他自己的私钥内容，则大家都无法还原完整的私钥地址。

　　所以在这种情况下，我们需要这5个人中只要有任意3个人在场就能还原私钥，而任意两个人在场不能还原私钥的方案。

　　这个方案就是编者今天要讲的比特币私钥共享方案。这种密钥共享的方式也被称为门限方案。【玩币族(http://www.wanbizu.com)专业币圈媒体】

　　门限方案设计

　　一般来说，门限方案可以具体的表示为(K，N)门限方案，即N个人中有任意K个提供密钥便可以还原整个加密内容，而任意K-1个人都不能还原整个内容。

　　因此上面的比特币私钥共享问题可以看作是(3，5)门限方案问题。

　　门限方案的设计多种多样，中国剩余定理、多项式算法、椭圆曲线加密算法等等都可以解决门限方案问题。

　　用中国剩余定理解决上面的(3，5)门限方案为例，编者可以取 53 、 59 、 64 、 67 、 71 这 5 个数，前面 3 个数乘起来得 200128 ，而后面两个数相乘才得 4757 。我们把文件的密码设为一个 4757 和 200128 之间的整数，比如 123456 。分别算出 123456 除以上面那 5 个数的余数，得到 19 、 28 、 0 、 42 、 58 。然后，把 (53, 19) 、 (59, 28) 、 (64, 0) 、 (67, 42) 、 (71, 58) 分别告诉这5个人，也就是说A只知道密码除以 53 余 19 ，B只知道密码除以 59 余 28 ，等等。这样，根据中国剩余定理，任意 3 人碰头后就可以唯一地确定出 123456 ，但根据任意2人手中的信息只能得到成百上千个不定解。例如，假设我们知道了 x 除以 59 余 28 ，也知道了 x 除以 67 余 42 ，那么我们只能确定在 0 和 59 × 67 – 1 之间有一个解 913 ，在 913 的基础上加上 59 × 67 的整倍数，可以得到其他满足要求的 x ，而真正的 M 则可以是其中的任意一个数。(参考资料 )

　　什么是中国剩余定理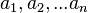

　　在(K,N)门限方案中，我们可以想办法构造这样一种情况， N 个数之中任意 K 个的乘积都比 M 大，但是任意 K – 1 个数的乘积就比 M 小。这样，任意 K 个除数就能唯一地确定 M ，但 K – 1 个数就不足以求出 M 来。

　　关于中国剩余定理详细请点这里

　　用多项式算法来解决(3，5)门限方案，在密码学中，我们有一些更精妙的方案。最巧妙的方法是，把私钥编码为三维空间中的一个点，然后生成5个过该点的平面，每个人持有其中一个平面方程。显然，任意两个人在一起是无法获得原文件的，因为两个平面的公共点有无穷多个;但三个平面的交点是唯一的，因此任意三个人在一起都能解开原文件。

　　用椭圆曲线加密算法来解决门限方案，专业人士请参见 。

　　比特币私钥共享方案设计

　　有了上面的门限方案后，比特币私钥共享方案设计就变得简单了。以上面的(3，5)私钥共享为例，我们采用第二种多项式的门限方案。

　　以16进制私钥为例:A90C28B2861B5D47F339599753A2387A86A79DBC88E7AAF0808D02B29C23F0BB

　　第一步、先把16进制私钥转化为10进制形式：1223397671331149484138190714211802661074685763175964491678362870066873941035952

　　第二步、再把10进制形式的私钥分解成三维空间的坐标点：

　　(12233976713311494841381，9071421180266107468576317596449167，8362870066873941035952)

　　第三步、将上面的值

　　x=12233976713311494841381

　　y=9071421180266107468576317596449167

　　z=8362870066873941035952

　　带入平面方程 Ax + By + Cz = D 中，并随机取五组(A，B，C)的值带入方程中，分别求出D。

　　例如，将A=2137897132，B=-321973913 ，C=-32139714434带入方程

　　则D=-2920760974123982275005673032587123377092347

　　第四步、将A,B,C,D的这组值告诉5人中的一人，并按照同样方法将计算出的值告诉其他4人。

　　这样，每个人手里面都有一个平面方程，任意三人都能算出交点的坐标，并重新组合成私钥。但是任意2人都求不出平面方程的交点(也就是x,y,z的值)，这样也就保护了私钥的安全性。

　　人数增多怎么办呢 如果共享密钥的人数增加，那么我们将采用更加复杂的密钥共享方案。密码学设计是一门很深的学问，希望编者的例子能给大家带来启发。（防采集链接：http://www.wanbizu.com/baike/201611027974.html）