| data availability(资料可取得性) 跟fraud proof (诈欺证明)对于区块链交易量扩展,是很重要的两项因素。当交易量大意味着资料量就变大(无论是分片或是加大区块大小),而资料量越大,能够运行全节点的人就会越少(因为硬体跟维护成本越高)。举例来说,Ethereum 2.0 有1024 条链,不可能每个人都把1024 条的资料都下载下来,更何况,这样也失去分片的意义,但若某节点做分片A 的validator,此时,需要跟分片B 有所互动,不太可能把分片B的所有区块都下载下来,太耗时也太占空间,而且若如此设计,最终也会把全部的链都下载下来….。但是,若没有全部的区块那要怎么验证交易呢?!这就是「资料可取得性」的重要性。 资料可取得性简单来说就是拿不拿得到资料,但不代表拿到的资料的有效的/正确的。那在讨论资料可取得性问题之前,先来认识诈欺证明。 在区块链世界中,验证资料方式可以分为有效证明(validity proof)跟诈欺证明两种。有效证明就是现在区块链的运作方式-「验证资料是正确的,才能上链」,也就是当你需要转帐时,矿工需要先验证你的余额是否足够,确认你余额是够的(验证资料是正确的)才会打包。而诈欺证明则是相反,验证者收到交易之后,经过一段时间若没有人提出异议/挑战,那就代表你送出的交易是没问题的,这种方式验证成本相对较低,也因此大部分L2方案选择使用诈欺证明作为资料验证的方式。 而轻节点只下载部分的资料(通常是block header),要如何能在运作上几乎跟全节点一样可靠呢('几乎'是因为轻节点需要额外的一些假设)?就必须借助资料可取得性跟诈欺证明的的合作。 Fishermen
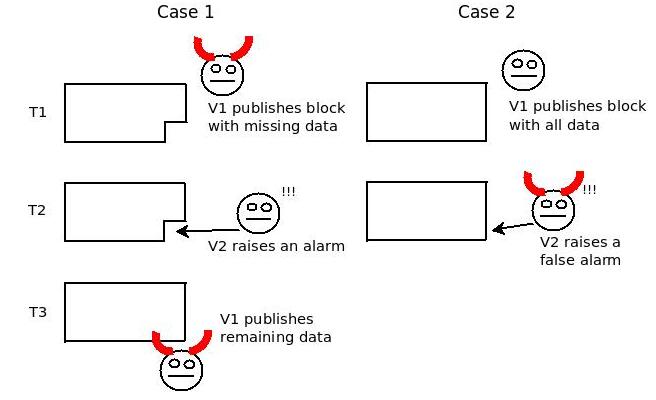
基本的奖惩机制如下, 1.若有人提出无效的诈欺证明,则没收押金, 2.若有人提出有效的诈欺证明,送出无效资料的人会被没收押金,而押金部份当作挑战者(提出诈欺证明的人)的奖励。 但是,这种机制在这个情境会有问题。我们来看以下这两个例子 Case 1: T1:攻击者v1送出不完整的资料(等待被挑战) T2: v2送出诈欺证明证明资料是无效的 T3:攻击者v1再补送剩下的资料 Case 2: T1: v1送出正确的资料 T2:攻击者v2发出无效的诈欺证明
如果渔夫打了个盹,没注意到T2 发生什么事,到了T3 才来验证,在这样的状况下是无法判断出两个的差异(因为T3 所能看见的就是”一份完整的资料”被提出”诈欺证明”,不知道其实case1 是后来补件的)。以上例来说,case1的v2 要给奖励吗?1.若给了,则攻击者就可以藉由发出无效的诈欺证明来赚钱(因为两着是无法分辨的)。2.若要惩罚,那就没有人愿意提出诈欺证明。3.若什么事都不做,则提供了一个免费的DOS 攻击。因此,这种方式有个根本的问题,就是无法有效遏止攻击者隐藏资料(因为被发现了,再补件即可),也就无法判断节点或是渔夫谁是恶意的。 
而merkle tree 的数量从原本的一个变成4*sqrt(M) 个(每个栏列皆为一个merkle tree,如下图所示)
接着,回到上面的例子,1MB的区块,每256bytes为一个区段,所以可以得到64x64的正方形,共有4*64个merkle tree,但是取样数就需要有48个,因此资料量为: 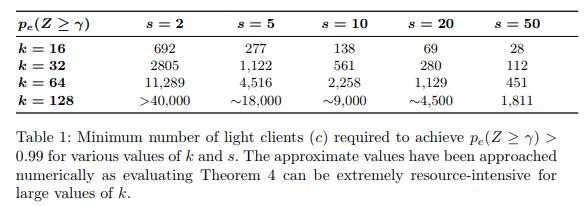
但若在一般的网路模式下,会知道自己的邻居们(peer nodes)是谁,所以对攻击者来说,就有空间操控,某个轻节点来问资料就故意不给,或是有时给有时不给等等的扰乱轻节点取得资料的稳定性。因此会需要搭配洋葱网路服用,攻击者就无法针对特定的轻节点作扰乱。再加上诈欺证明的挑战,在整个设计中只需要保证网路中有一个诚实节点即可。 
这是目前Ethereum 2.0 轻节点的提案,#1194是针对资料可得性证明效率不足的讨论,主要的问题在于,二维的纠删码让处理的资料量变大,也增加网路传输的负荷,再加上EIP1559,将使得区块平均的负载量约只有50%,也就意味着需要填很多的0,让二维纠删码徒增很多无意义的数据,这也是目前尚未解决的问题。 —- 编译者/作者:不详 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
以太坊2.0轻节点上的数据可用性
2019-07-10 不详 来源:网络
- 上一篇:挖矿造成伊朗电耗增长7%,能源部官员发出警告
- 下一篇:李启威:莱特币会“死掉”?
相关阅读:
- 瑞波首席执行官布拉德·加林豪斯(Brad Garlinghouse)反对Coinbase的“不政2020-10-26
- Pionex派网携手币安,全新交易工具开启「区块链券商」新赛道 - 律动B2020-10-26
- Binance Launchpad添加了游戏宠物宇宙Axie Infinity2020-10-26
- 物联网区块链平台 IoTeX 将于 11 月 3 日上线「销毁空投」计划,将共销毁2020-10-26
- 〔YAS你问我答,第两百三十九篇〕play是主网平台币,等同于yas2020-10-26