前言 Bulletproofs,又一个有意思的零知识证明算法,相信读者已经很熟悉它了。和zk-snark相比,它不需要可信设置;和zk-stark算法相比,它具有较小的proof size。根据论文,它有两个方面的应用:1. 用于range proof;2. 用于一般算术电路的零知识证明。下面,让我们先看一下Bulletproofs是如何高效的实现第一点。 Range proof 1.?预备知识 aL:表示向量{a1,a2……an} 2n:表示向量{20,21…2n-1} <a, b>:表示向量内积 ∑ ai*bi,结果是一个值 a o b:向量对应位相乘,{a1*b1……an*bn},结果是一个向量 2.?证明 Alice想要证明 v ? [0, 2n-1] =>则,需要证明一个relation得成立,如下所示: {(g、h ? G,V,n;v,r ? Zp):V = grhv ^ v ? [0, 2n-1] } public-xwitness-w relation-R 即,对于公开信息x,Alice有隐私信息w,使得关系R成立。 令 aL为金额v的在范围[0, 2n-1]内的二进制形式,则aL = {a1,a2……an}?{0,1}n,且满足<aL, 2n> = v。因此,证明者需要证明以下几个等式相等: V = grhv(1) <aL, 2n> = v(2) aL o aR = 0n(3) aR = aL - 1n(4) 等式(1)确保了承诺V和金额v的绑定关系,等式(2)确保了v的范围,等式(3)(4)确保了aL 元素只属于{0,1}。等式(2)/(3)/(4)总共包含了2n+1个约束,其中公式(2)1个,公式(3)(4)各n个。接下来,为了效率,我们需要把2n+1个约束转换成1个约束。 3.?2n+1个约束转换成1个约束=>预备:从Zp中任意选择一个数y,则b = 0n是等式<b, yn> = 0成立的充分条件;因为当b != 0n,等式成立的概率仅有n/p,p是有限域,远大于n。(理解:如果b != 0n ,把等式看作求n阶一次多项式的零点即可)因此,如果有<b, yn> = 0,那么验证者愿意相信b != 0n 。 利用这个理论,我们把等式(2)/(3)/(4)做以下转换: 1. 验证者随机选取一个数y发送给证明者; 2. 证明者要证明: <aL, 2n> = v (5) <aL , aR o yn> = 0(6) <aL - 1n- aR, yn> = 0(7) 同理,等式(5)确保了v的范围,等式(6)(7)确保了aL 元素只属于{0,1}。此时2n+1个约束转换成3个约束,接下来,还需要做进一步的处理:1. 验证者随机选取一个数z发送给证明者: 2. 证明者利用z对公式(5)(6)(7)进行线性组合,得到如下公式: z2 * <aL, 2n> + z * <aL - 1n- aR, yn> + <aL , aR o yn> = z2 * v(8) 至此,我们已经把2n+1个约束转换成1个约束。下面我们对公式(8)做进一步的优化,把三个点积优化成1个点积 4.?三个点积优化成1个点积=> z2 * <aL, 2n> + z *<aL - 1n- aR, yn> + <aL , aR o yn> = z2 * v => <aL, z2 * 2n> + <aL, z * yn> - <z * 1n, yn> - <z * aR, yn> + <aL , aR o yn> = z2 * v => <aL , aR o yn + z * yn + z2 * 2n> - <z * 1n , yn> + <z * 1n, yn o aR> = z2 * v => <aL , aR o yn + z * 1n o yn + z2 * 2n> - <z * 1n, yn + yn o aR> = z2 * v => <aL , (aR + z * 1n) o yn + z2 * 2n> -<z * 1n, yn + yn o aR> = z2 * v => <aL , (aR + z * 1n) o yn + z2 * 2n> -<z * 1n, (aR + z * 1n) o yn + z2 * 2n -z * 1n * yn + yn - z2*2n>=z2 * v =><aL - z * 1n, (aR + z * 1n) o yn + z2 * 2n> - <z * 1n , -z * 1n * yn + yn - z2*2n> =z2 * v =><aL - z * 1n, (aR + z * 1n) o yn + z2 * 2n> = z2 * v + <z * 1n , -z * 1n * yn + yn - z2*2n> =><aL - z * 1n, (aR + z * 1n) o yn + z2 * 2n> = z2 * v + <z * 1n , (-z * 1n + 1n) * yn > - <z * 1n ,z2*2n> =><aL - z * 1n, (aR + z * 1n) o yn + z2 * 2n> = z2 * v + (z – z2) * <1n, yn> - z3 * <1n, 2n>(9)
=>令 L =aL - z * 1n R =(aR + z * 1n) o yn + z2 * 2n δ =(z – z2) * <1n, yn> - z3 * <1n, 2n> 5. 验证: 1. 证明者把L/R/V发送给验证者; 2. 验证者事先算好 δ 3. 验证者根据L算出来aL,根据<aL, 2n> = v算出v 4. 验证者根据L,R,v,δ验证等式<L, R> = z2 * v +δ 因为y,z都是验证者提供,因此如果验证者如果能验证公式(9)成立,则相信等式(5)(6)(7)成立,则相信等式(2)(3)(4)成立,则相信v满足关系v ? [0, 2n-1]。 但是,可以看到上述过程,泄露了v的信息,因此需要一个零知识证明协议。 6.一个零知识证明协议 由于L,R包含了v的相关信息,因此,我们需要添加两个盲因子sL、sR来隐藏aL,aR。如公式(10)(11)所示: l(X) = (aL - z * 1n) + sL * X )(10) r(X) = (aR + z * 1n + sR * X) o yn + z2 * 2n(11) 此时,定义公式(12)t(X) = <l(X), r(X)> = t0 + t1*X + t2 * X2(12) 可以看出系数t0是l(x)和r(x)常数项的乘积,即满足:t0 = <L, R> = z2*v + δ 因此,问题由证明:<L, R> = z2*v + δ 转化成了,在任意一点x,验证者验证多项式值l(x), r(x), t(x)满足关系:<l(x), r(x)> = t(x) 多项式值l(x), r(x), t(x)由证明者提供,为了保证l(x),r(x) well-formed,即:l(x) = (aL - z * 1n) + sL * x ) r(x) = (aR + z * 1n + sR * x) o yn + z2 * 2n 需要校验:P = A * Sx * g(-z) *(h`)z*yn+z^2*2^n = hαgaLhaR * (hρgsLhsR)x * g(-z) * (h`)z*y^n+z^2*2^n = hαgaLhaR *hρxgsL*xhsR*x * g(-z) * (h`)z*y^n+z^2*2^n = hα+ρx * gaL+ sL * x – z * 1^n * haR + sR * x * (h`)z*y^n+z^2*2^n = hα+ρx * gaL+ sL * x – z * 1^n * (h`)y^n o (aR + sR * x) * (h`)z*y^n+z^2*2^n = hα+ρx * gaL+ sL * x – z * 1^n * (h`)y^n o (aR + sR * x) + z*y^n+z^2*2^n = hα+ρx * gaL+ sL * x – z * 1^n * (h`)y^n o (aR + sR * x + z * 1^n) + z^2*2^n =? hμgl(h`)r => 当且仅当l/r well-formed,等式成立 为了保证t(x) well-fromed,即: t = t0 +t1x + t2x2 需要校验:=> gthτx =? Vz^2 * gδ*T1x *T2x^2 => gthτx =? (hrgv)z^2 *gδ *(gt1)x*(hτ1)x*(gt2)x^2*(hτ2)x^2 => gthτx =? hz^2*r + τ1*x + τ2*x^2 * gz^2*v + δ + t1*x + t2*x^2 => gthτx =? hz^2*r + τ1*x + τ2*x^2 * gt0 + t1*x + t2*x^2 => t = ? t0 + t1*x + t2*x2 && τx = ? z2*r + τ1*x + τ2*x2 => 当且仅当t和τx welle-formed,等式成立 具体的协议流程图如下图所示:
—- 编译者/作者:江小白 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
技术干货 | 理解零知识证明算法之Bulletproofs:Range Proof I
2019-12-13 江小白 来源:区块链网络
- 上一篇:年内比特币暗网成交额已超10亿美元 相比去年有望翻倍
- 下一篇:生活意义
LOADING...
相关阅读:
-
暂无相关文章

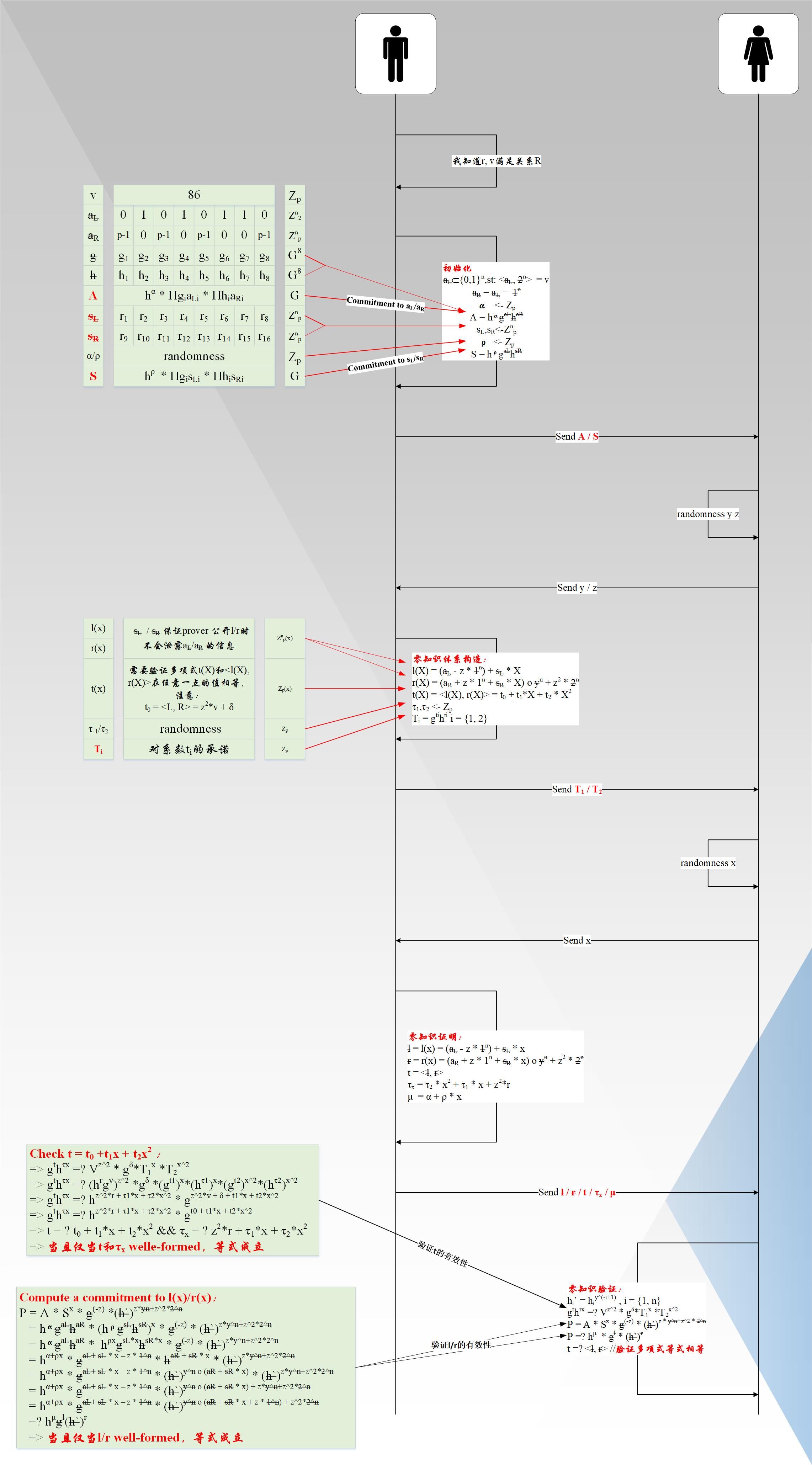 总结
从上述流程可以看出,一次range
proof,证明者需要发送总共{ l / r / t / τx / μ / T1 / T2/
A / S}个元素给验证者,总共2n+3个Zp元素,4个G元素。下一篇文章将细讲,Bulletproofs如何将交互复杂度降低到对数级O(log(n))
附录
1.
Bulletproofs
论文:chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Feprint.iacr.org%2F2017%2F1066.pdf
总结
从上述流程可以看出,一次range
proof,证明者需要发送总共{ l / r / t / τx / μ / T1 / T2/
A / S}个元素给验证者,总共2n+3个Zp元素,4个G元素。下一篇文章将细讲,Bulletproofs如何将交互复杂度降低到对数级O(log(n))
附录
1.
Bulletproofs
论文:chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Feprint.iacr.org%2F2017%2F1066.pdf