原文标题:《以太坊核心开发者:MPT 十六叉树将被替换》 想象一下,你正在翻译一本 5000 页的书籍,作者一直打电话告诉你他对故事做了调整,这会影响到你已经翻译过的页面……而这可能会一直持续下去,这就是以太坊从当前使用的 MPT 十六叉树转变为二叉树结构中遇到的一个类似困境。对此,以太坊核心开发者 Guillaume Ballet 提出了一种方案,可以在大约几天的时间内,通过 3 个步骤完成这一转换手术。
对于该提案,以太坊联合创始人 vitalik 评论称:
以下是译文: 影响以太坊的众多问题之一是账户和合约数据的存储方式,以太坊目前选择的结构称为默克尔帕特里夏树 (Merkle Patricia Tree,或简称 MPT)。尽管从理论上讲,它是很有意义的,但在实践中,它带来的问题要比其解决的问题要更多。多年来,核心开发人员一直在讨论向二叉树(binary tree)的转换,在本文中,我将阐明我对这一问题的看法,然后给出一个解决它的方法。 提议的过程引入了一个过渡期,在此期间,两种树结构都会存在。这样做的好处是,在转换树结构时,主链可以保持运行,并且还可以确保将所有帐户转换为二叉树格式。 背景 目前,以太坊的账户是被存储到一棵十六叉树当中的。所谓十六叉,就表示一个节点有 16 个子节点,理论上这是很好的,因为这意味着你需要更少的「阶段」来存储你所有的数据。 例如,这就是以十六叉树的形式表示键与值对(170,v)的过程。在十六进制中,170 表示为 0xaa,因此你只需要两层:其中之一用于第一个 a,另一层则用于第二个 a。
注意,这棵树很浅,也很宽。然后将其与以下相同键与值对的二叉树表示法进行比较。在二进制中,170 表示为 10101010。
你可以看到,这棵树要深得多,也窄得多。 在以太坊中,每个区块都包含一个 stateRoot 字段,它是 MPT 根的哈希值。总而言之,这个哈希,是通过对根的 16 个子项的哈希列表进行哈希运算而获得的。这些子哈希列中的每一个,又依次是其子哈希列表的哈希,依此类推。 每次生成一个新区块时,矿工都会更新帐户树并重新计算其根哈希值。哈希存储在新区块的 stateRoot 字段中,然后新区块被密封。
问题就出现在这里了:通过对所有节点进行哈希运算来重新计算哈希根花费的时间太长,因此,为了计算根节点,矿工将从数据库中检索同级哈希(sibling hash)。尽管从数据库中获取所有子叶并对整棵树进行哈希运算所需的时间不多,但此操作仍然需要大量时间。这是因为必须要从数据库中获取每个哈希。 在十六叉树中,通常每个阶段要获取 15 个同级哈希。在上面的示例中,这就是 30 个哈希。 即使更深入,二叉树每个阶段也只需要一个同级哈希。在上面的示例中,就只有 8 个哈希!这就是为什么在实践当中,二叉树实际上要更好的原因。 覆盖转化法 不幸的是,要将以太坊从十六叉树切换到二叉树,并不是一件容易的事。有很多数据需要转换,并且执行更改需要花费超过 15 秒的区块时间。 除此之外,想象一下,你正在翻译一本 5000 页的书籍,作者一直打电话告诉你他对故事做了调整,这会影响到你已经翻译过的页面……而这可能会一直持续下去。 这就是目前以太坊遇到的问题,因为用户可以更新已转换的地址,这意味着你必须重新开始转换过程。 解决此问题的建议是设一个过渡期,在此期间,在十六叉树的顶部放置一棵覆盖二叉树,它的作用是保存状态发生的所有更改,直到基树转换为二叉树。 这种过渡会分成三步进行: 第 1 步-转换 在这种方法中,确定在区块高度 H1 处,区块具有两个 stateRoots:一个用于「基础」十六叉树,一个用于「覆盖」二叉树。
十六叉树被认为是只读的,因此对状态的任何更新都将是对覆盖树的更新。 当一笔交易读取或更新一个帐户时,系统首先搜索覆盖树。如果在那里找不到帐户,系统将在旧的十六叉树中搜索该值。 而在同时,十六叉树正在后台转换。现在可以不用担心插入,因为所有更改都存储在顶部树中。 第 2 步-基转换 后台转换过程完成后,矿工将通过转换结果替换只读的十六叉树基础根来宣布他们已准备好进行切换。对状态的读写操作与步骤 1 相同。
当一个足够大的序列区块对转换后的基础根具有相同的值时,这意味着大多数矿工都完成了转换,并对转换后的树的外观达成了共识。接下开,就进入到合并过程。 第 3 步-合并两颗树 合并过程会逐渐进行:每次生成新区块时,都会从叠加层中删除 n 个键,然后将其重新插入到基础树中。该过程将持续进行,直到从叠加层中删除所有键为止。在此阶段,覆盖状态根将从区块头中删除。 除此之外,如果交易执行写入覆盖树中找到的键,则该键将从覆盖树中删除,并直接写入到基础树。 下一步 我们已经创建了一个 初步的原型,以便估计完成转换所需的时间。我们相信,整个过程可以在合理的时间内(大约几天)完成。随着算法的改进,我将发布更多的细节。 致谢 这项提议得益于 Alexey Akhunov,Vitalik Buterin,Anna George,Sina Mahmoodi,Tomasz Stanczak 以及 Martin H. Swende 提供的宝贵意见。 相关讨论 来源链接:medium.com —- 编译者/作者:巴比特资讯 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
以太坊核心开发者:MPT 十六叉树替换成二叉树只需要三步
2020-03-30 巴比特资讯 来源:链闻
LOADING...
相关阅读:
- 德国中央银行同意这个区块链项目2020-10-31
- 贤哥懂币:10.31以太坊行情分析及走势2020-10-31
- 未来没有发达国家,只有数字化国家‖比特币也许是泡沫,但区块链一2020-10-31
- 在意大利机场发现非法采矿场2020-10-31
- 他的预测是正确的,分析师宣布山寨币值得关注并期待比特币?Coinkolik2020-10-31

 图片来自:tuchong.com
图片来自:tuchong.com
 图 1: 这是一棵十六叉 trie 树示例,显示了值「v」如何存储在键 0xaa 处。此树只有 2 字节长的键,并且只沿 0xaa 键的子树被展开。为了简洁起见,不相关的子树被替换为「…」
图 1: 这是一棵十六叉 trie 树示例,显示了值「v」如何存储在键 0xaa 处。此树只有 2 字节长的键,并且只沿 0xaa 键的子树被展开。为了简洁起见,不相关的子树被替换为「…」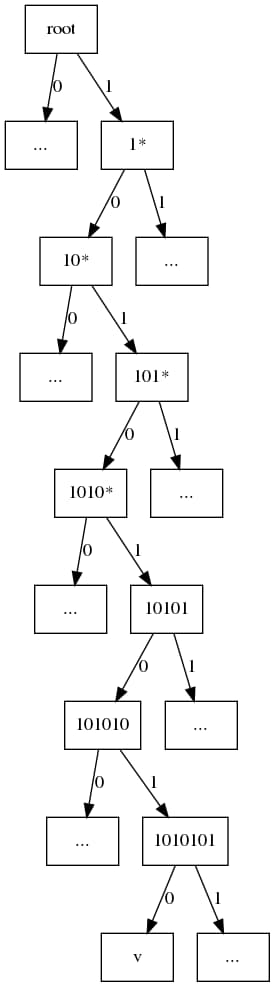 图 2: 和图 1 中相同的键值对,以二叉树形式进行存储。为了简洁起见,不相关的子树被表示为「…」
图 2: 和图 1 中相同的键值对,以二叉树形式进行存储。为了简洁起见,不相关的子树被表示为「…」 图 3 区块头的 state root 字段指向十六叉树的根
图 3 区块头的 state root 字段指向十六叉树的根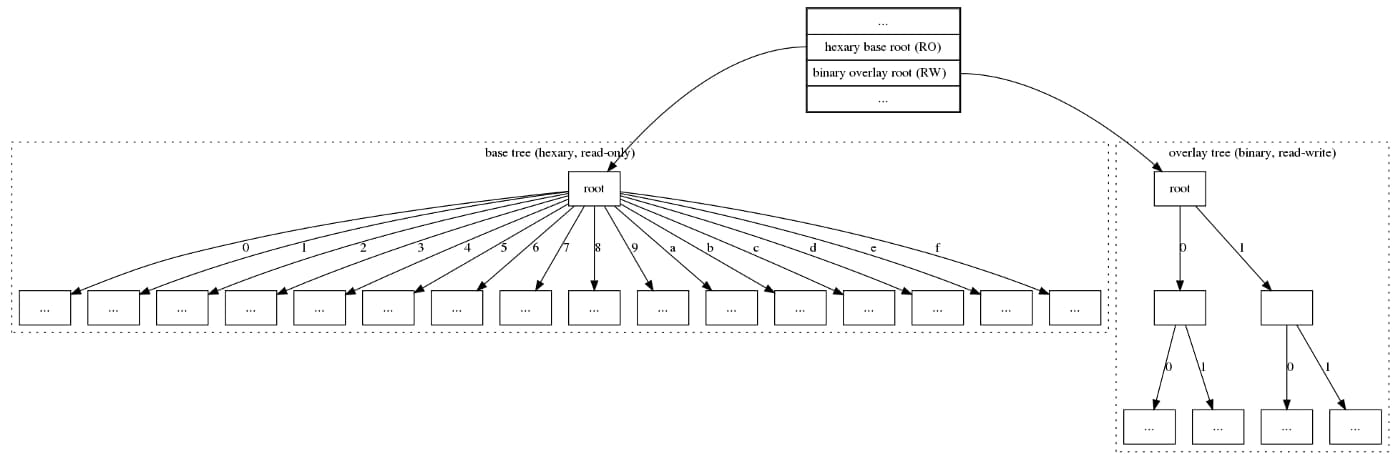 图 4: 在转换过程中,区块具有 2 个状态根(state Root):一个是传统十六叉树的只读根,第二个是「覆盖」二叉树的根
图 4: 在转换过程中,区块具有 2 个状态根(state Root):一个是传统十六叉树的只读根,第二个是「覆盖」二叉树的根 图 5: 转换的第二个阶段,区块头将十六叉树基础根替换为其二叉树转换基础根,以向网络发送信号,告知它们已准备就绪
图 5: 转换的第二个阶段,区块头将十六叉树基础根替换为其二叉树转换基础根,以向网络发送信号,告知它们已准备就绪