当前位置: 玩币族首页 > 新闻观点 > 幂率法则：比特币价格能预测吗？

幂率法则：比特币价格能预测吗？

2020-05-29 NewBloc 来源：区块链网络

文 / New Bloc 基金经理李福星

幂率法则

1932年，生物学家克莱伯（Max Kleiber ）做了一组实验。他将各种哺乳动物称重，从200吨重的蓝鲸，到几十克重的小老鼠，以体重作为横坐标，以动物们在单位时间内呼出的二氧化碳转换出来的新陈代谢率作为纵坐标，做出双对数坐标图（纵横坐标皆取对数）。做出图之后，仿佛九星连珠一样的景象出现了：所有动物都站在了一条直线上！

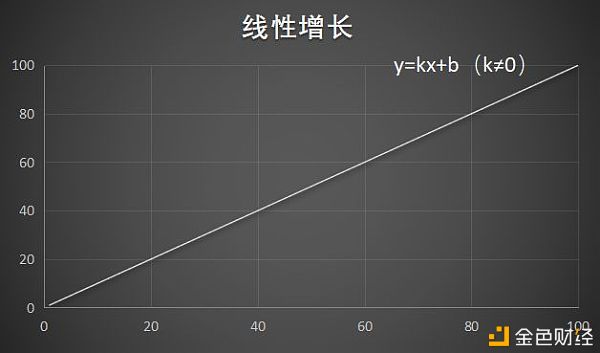
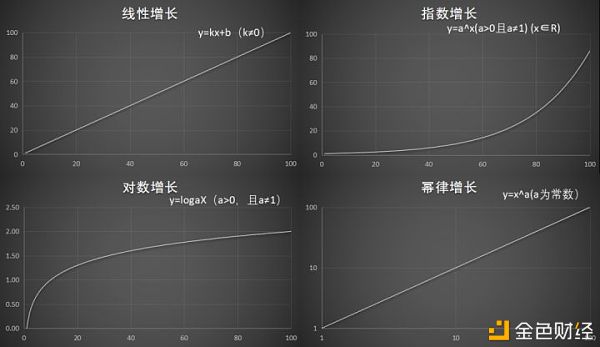
erechos: Tasas metabólicas basales de varios animales. UV.

21世纪以来，生物学家们继续测量，惊讶地发现这个规律的适用领域横跨了30个数量级：小到线粒体、细胞级别的低等生物，大到最大的哺乳动物，跨度如此之大的物种，都能站到这条线上——斜率3/4。这么多种不相干的动物，整齐划一地遵从了数学规律。

这就是克莱伯定律（Kleiber's law）：对于哺乳动物，其基础代谢率与体重的3/4次幂成正比即。用优美简洁的数学公式表示，就是?F=c·M^?

F : 物种平均新陈代谢

M: 物种平均体重

c : 和环境温度有关的系数

来源于圣经马太福音的马太效应、描述个人财富分布的帕累托法则（80/20定律）、描述书籍中单词频率分布的齐夫定律（Zipf's law）、统计物理学中的无标度网络模型、商业领域的长尾理论、不确定性研究领域的黑天鹅——追索到源头，都有一个共同的数学规律：幂律法则（Power Laws）。

这些来自社会学、哲学、物理学、语言学、生物学、经济学中的Lows，本质上都是幂函数在不同学科的体现，这种分布规律就是幂律分布（Power-Law Distribution）。

实际上，幂律分布不仅限于这些领域，还在地球科学（地震规模）、天文学（月球环形山、行星碎片、太阳耀斑）、计算机科学（文件大小）、生态学、军事学（战争规模）、神经科学（神经元活动模式）、人口统计学（姓氏分布）、社会学（城市规模、专利数量）、金融学（银行坏账、投资回报、股市崩盘）领域广泛存在。人们已经发现了无数个幂律分布的案例。总结起来，这些领域是：

缺少增长约束（微博粉丝数、财富分配）

增长迅速，跨越多个数量级（增长稳定期之前的细菌、月球环形山规模）

系统内个体之间有关联（奥运会得奖数量、城市规模、投资回报）

幂律分布在双对数坐标下表现为一条直线，其斜率是幂指数的负数，方程式为：

y=b·x^a

这么多学科、看似风马牛不相及的事情，本质上都服从于幂律法则，用一条数学公式就可以简洁概括。整个宇宙包括人类社会都布满了这个公式。幂律无处不在。幂律分布有一个很直观的展示方式：对数坐标。在对数坐标下，幂律分布呈现出一个非常简洁的直线。这个可以从函数公式中得到解释。幂函数公式 y=b·x^a，两边同时取对数

logy = logb + a·logx → y'=ax'+b'

这样一来，非线性的幂函数，就变成了线性关系。所以在对数坐标下，表现出来的就是直线一条。这种在对数坐标下的线性关系，是判断一个随机变量是否满足幂律的根据。与普通坐标相比，对数坐标按照指数增长来表示，将大堆看似无序的信息统一在一起，消除了很多噪音。信息的本质就是消除不确定性，这样的处理得到了一个平稳的序列，为研究分析提供了巨大的便利。

线性增长

我们生活中常见的是线性思维，线性增长。比如一分耕耘一分收获，种瓜得瓜种豆得豆，多劳多得。在时间序列上，增长方向保持一致，增长速度基本保持匀速。

在线性坐标系下，所有数据排成一条稳定的直线。在统计学中，“确定系数”被用来描述这些数据的有序程度，用R?表示，反应了”因变量的全部变异能通过回归关系被自变量解释的比例”。说人话，就是如果R?为0.99，那么99%的数据可以用这条直线表现出来的趋势来解释。举个栗子，我常用的场内货币基金银华日利，是个典型的线性增长的例子。上市6年来，不急不缓，每年3.5%的收益。

数据来源：同花顺把价格导出来，拟合一下，R?=0.9946，就是一条直线。

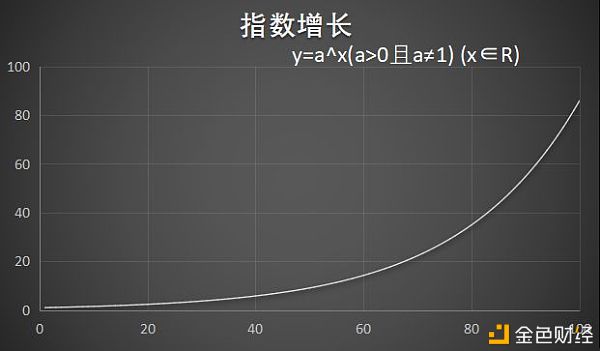
数据来源：Wind资讯再比如，很多工作岗位的收入是线性增长的。门卫、司机、前台、行政，政府工作人员，大部分教师、医生、护士，普通文体教练等。这些工作岗位主要以工作时间计价，其收入是线性增长的，确定性很高，稳定。这种收入波动很低，收入的增长依赖于时间的付出，就是俗话说的一眼看到底。但是，也有很多东西并不能按照线性增长。比如一只有10万的人，赚1万很开心；有100万之后，赚1万的幸福感就差远了。这就是线性增长的缺点。这种情况下，或许再赚100万差不多会同样开心，因为增长率相同。这就用到了指数增长。指数增长指数增长又称“几何增长”。因为在几何中，面积与边长的关系是乘积的函数关系（三角形的面积S=a·H/2），很形象地表达了一个数以固定的比例增长。最重要的应用之一，就是复利。指数增长按照固定的增长率发展，随着时间推进，基数变大，增长规模迅速膨胀。正所谓行百里者半九十。指数增长是固定比例增长，不是每天进步一点点，是每天进步相同比例，复利。但是，如果Y轴用对数坐标，指数增长将会表现为一条直线。

举个栗子。贵州茅台的股价，在行情软件上用常见的线性坐标看，是典型的指数增长，最近两年上涨太快，下不去嘴（下图蓝线）；如果把Y坐标轴改用对数坐标，就会发现上涨趋势并没有明显变快（下图黄线），除去2005~2007年市场整体泡沫的历史时期，股价始终在拟合线附近。这条拟合线，确定系数R?高达0.90。股价的变化当然要用对数坐标，因为复权后，5元钱的茅台涨到7.5元，和1000元的茅台涨到1500元，是一样的涨幅。

数据来源：Wind资讯我国1960年以来的GDP规模，也是个典型的指数增长，刚开始规模不大，进展缓慢，21世纪以来飞速上涨，生产力彻底解放了。

因为这两年 GDP 的速度放缓，各种崩溃论又出来了。如果我们把Y轴改成对数坐标，就会发现并没有什么可怕的。GDP 一直沿着直线上涨，R?高达0.9649，上涨速度在历史上都不算坏。

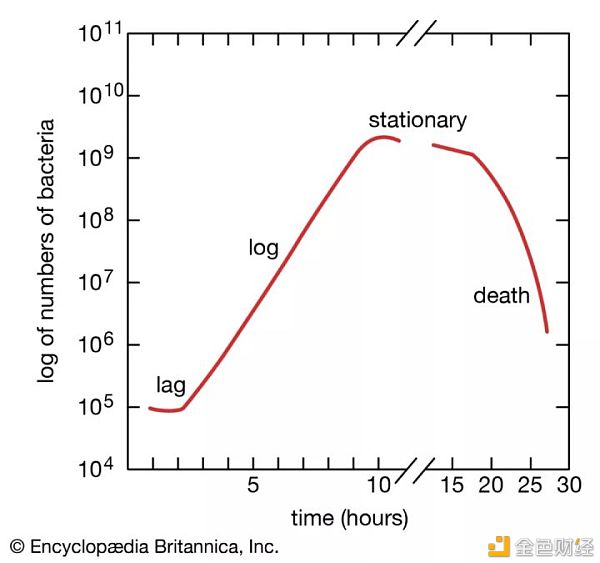
简单来说，用指数坐标这种表达方式，在克莱伯的实验中，可以把“小老鼠体重由10克增加到20克”和“大象体重由1吨增加到2吨”这两件事情放在同一维度中，研究其变化规律。对数增长但是，很少有事物能一直保持指数增长。事物的增长，在数量级小的时候，只需要很少的能量/时间，带来的增长就可以很迅速；随着时间推移，体量变大，需要募集、消耗更多的能量。所以，增速逐渐衰减，无限接近增长的极限，甚至最终走下坡路，也是自然法则。我上次写过细菌培养实验，指数增长只能维持一定时间周期，最终受制于环境、自身免疫等，增长率会下降。

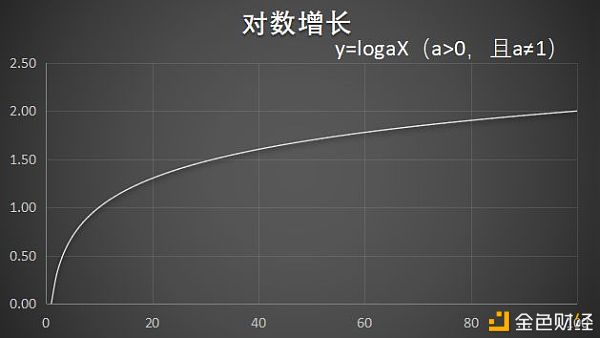
这种增长相同数量需要更多时间/资源的增长方式，就是对数增长。

举个栗子。跑马拉松、学习外语、弹钢琴，这些技能入门很简单，短时间内增长迅速，越到后面提高越困难。所以，运动员、作家、艺术家这些，在达到一定水平之后，都需要更加漫长的时间，才能到达一个更高的层级。芒格说，巴菲特每天看书5小时，直到在60岁之后，投资技艺才炉火纯青。区分庸人和专家/大师的界限也在这里，这是很多人少年得志，成年后却伤仲永的原因。幂增长最能持久的增长方式，回到开头的克莱伯定律，就是幂率增长。简单来说，取得一个数量级的增长，需要相应付出一个数量级的时间/资源。这种幂律增长可以维持很久。

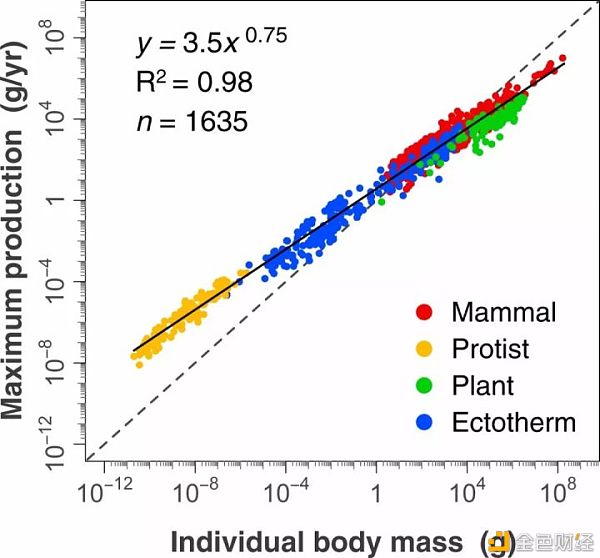
在生态学中，有个捕食者-食饵模型，其中生物量在生物群落中的尺度变化，就是符合幂率增长。

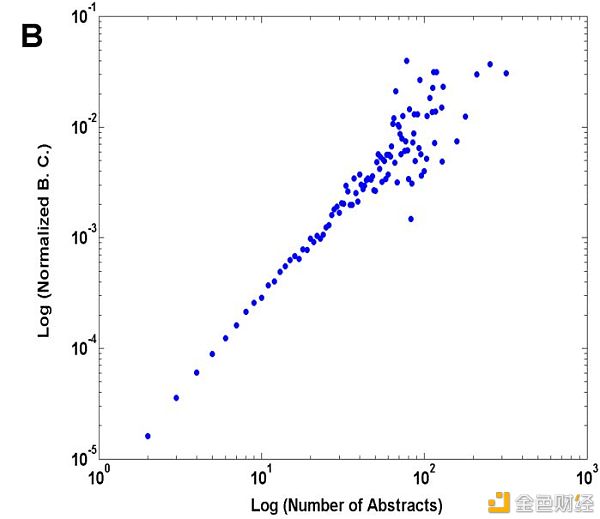
The predator-prey power law: Biomass scaling across terrestrial and aquatic biomes

还有，一些论文作者的中心地位和论文被引用数量，也遵循幂律法则。

An Analysis of the Abstracts Presented at the Annual Meetings of the Society for Neuroscience from 2001 to 2006

Ok，此刻我又想到了比特币。比特币符合哪种增长？

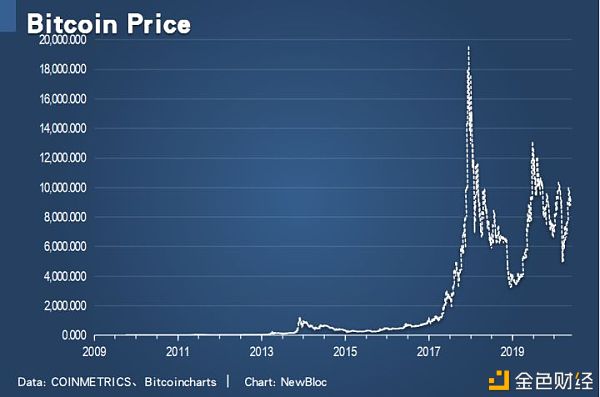
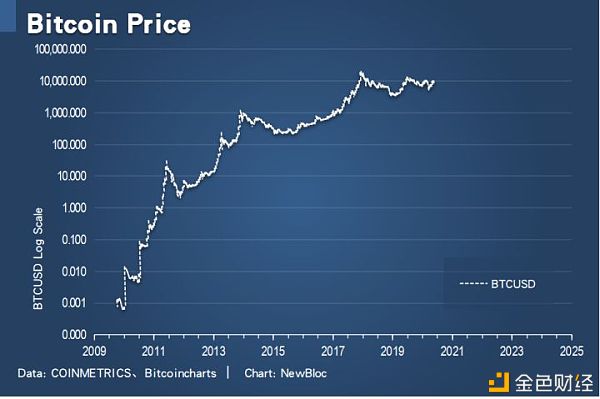
线性坐标下的秘密首先，在最常见的线性坐标下，大饼价格走势看起来极度无序，跟银华日利完全不同。显然这不符合线性增长，这又不是银行存款。在线性坐标下，大饼的价格大开大合，涨则几十几百倍，一跌就是腰斩、膝斩、脚踝斩。这种线性坐标显示的币价，也是媒体上最常见的价格图，经常被各种人用来对比特币冷嘲热讽，几乎成了比特币就是CX的证据。

在业内，分析师们最常用的就是将Y轴取对数。在这种单对数坐标下，比特币价格看起来有序多了，有种让人数浪的冲动。目前，市场上很多分析师在此基础上发展了各式各样的分析模型。

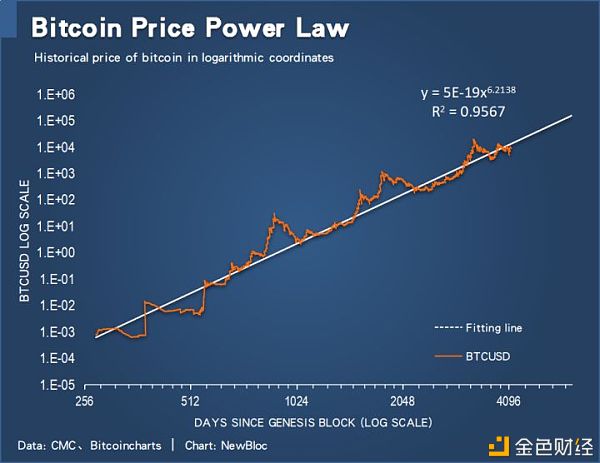
可以看出，对数坐标给分析工作带来很多好处：第一，将比特币多个数量级的价格统一到一致的观察维度中；其次，可以观察到比特币最早期的价格发展轨迹，看到早期人们赋予大饼的定价（小老鼠），而非仅仅是最近变化剧烈的价格（蓝鲸）；第三，有利于寻找币价变化深层次的线性规律，分析研究底层的数学原理；第四，去除线性坐标中杂乱的价格噪音，发现背后真实的信息，降低一个分析维度；

最后，越过价格波动的集群效应，削弱历史价格中隐藏的异方差和共线性，便于从整体研究价格波动规律。如果是指数增长，那么比特币价格表现出来应该是一条向上倾斜的直线。很明显，在Y轴取对数下，币价最近五年明显放缓。比特币价格不符合对数增长。

比特币 ∈ 幂率法则

那么，双对数坐标会怎样呢？以比特币出生的2009年1月3日记为1，每过1天增加1个数，以这个自然数列——比特币诞生天数作为x轴编制走势图，然后对其取对数——见证奇迹的时刻：

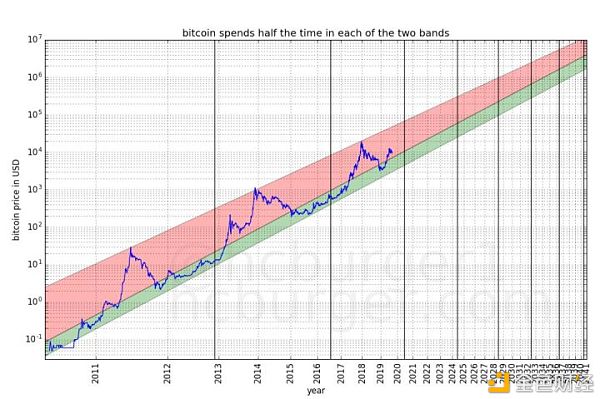
几乎所有的比特币历史价格，都乖乖站成了一排。做了一下线性回归——是一条倾斜向上的直线，R?=0.9567！也就是说，从比特币出生那天开始，历经10年的涨涨跌跌，95.67%的历史价格都包含在这条直线揭示的趋势中。比特币价格呈现非常标准的幂率增长！

如此一来，价格曲线就非常整齐了：多个数量级的变化看清了，早期的成长轨迹清晰描述出来，线性规律非常明显，噪音背后的信息水落石出，降低了异方差和共线性的影响。去年秋天，比特币分析师 Harold Christopher Burger 就这个主题写了一篇广为流传的文章，以2010年7月门头沟价格开始，做了一张双对数坐标图：

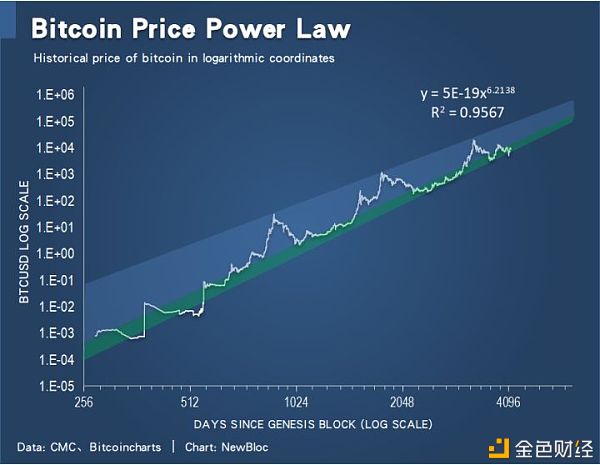
Bitcoin’s natural long-term power-law corridor of growth，Harold Christopher Burger

Burger取到的拟合线，R?=0.9314；我加入了2009年10月5日到2010年7月16日这段时间的 New Liberty Standard 电价模型价格，线性回归后得到的R?=0.9567，比 Burger 的图还要线性。

我按照自己的审美，也画出了这个长期价格走廊。

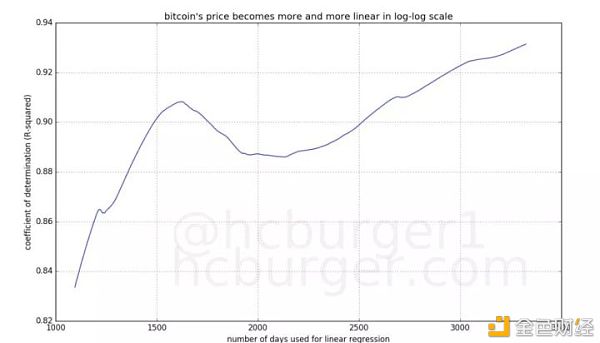
R?=0.9567，我相信这不是巧合。价格与时间之间存在明确的幂律关系，

这是巧合的概率极低。

Burger还把确定系数的历史变化统计了一下，结论是：这个模型越来越倾向于更好地拟合币价！

Bitcoin’s natural long-term power-law corridor of growth，Harold Christopher Burger

也就是说，10年来，比特币的价格越来越符合幂律法则。Burger依据这个价格走廊作了预测：价格在2021年前无法达到10万美元，但2028年后不会低于10万美元。价格不会在2028年前达到100万美元，但2037年后不会低于100万美元。预测，我觉得还是不要了。这里把玩的只有价格、时间两个维度，对分析一个市场来说，还远远不够。这些价格通道并不能直接作为对行情进行展望的依据。不能犯了归纳法中典型的“感恩节火鸡”之谬。当然，从另一个逻辑出发，历史对未来是有启发意义的。比特币的普及度、稀缺度、价格周期运动等，有很大一部分信息已经高度概括在过去11年的价格中。所以，币价透露出的幂律法则，值得认真研究。