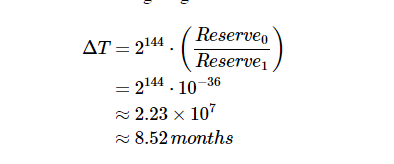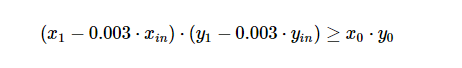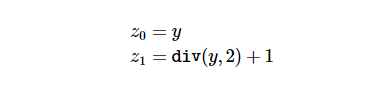Uniswap V2 审计报告

概要

从2020年1月8日到4月30日，一个由6名工程师组成的团队审查并正式验证了Uniswap去中心化交易协议第二版智能合约的关键组件。

这项工作是针对以下git仓库进行的:

在此期间，发现了两个中风险问题:

Pair:固定流动性通缩引入竞态条件Router:不兼容代币转账手续费

此外，还进行了一些小的改进，提高了gas燃料效率。

完整的发现列表可以在这里找到。

在此过程中，在uniswa -v2-core仓库中发现的所有问题都在提交版本8160750中得到了解决。

团队建议在上线前对最终版本的外围合约进行更多的分析和审查。

范围

核心智能合约的正式验证

使用act规范语言和K框架生成了uniswap-v2-core仓库中智能合约（命名为UniswapV2Pair和UniswapV2Factory）的方法级正确性的正式规范和证明。

关于正式规范及其证明状态的概述可以在dapp.ci/k-uniswap的审计组CI系统中找到，关于提出的证据的性质的讨论可在本报告的正式验证部分找到。

核心智能合约的代码审查

审计组对uniswap -v2-core智能合同进行了一般的代码审查和安全分析，发现了2个漏洞:

一个中风险问题 Pair:固定流动性通缩引入竞态条件一个低风险问题Math:sqrt中的整数溢出

以及一些关于gas燃料优化和代码清晰度的建议，这些都在调查结果中详细介绍。

这些改进大部分被Uniswap开发团队采纳。

数值误差分析

审计小组审查了合约执行过程中产生的数字误差，重点放在Uniswap开发团队提出的理想的恒量(例如，舍入误差，如果在兑换有则有利于资金池)。

团队没有发现任何位置的数值错误违反这些恒量，另外在固定精度设置上针对巴比伦平方根算法产生了一个新的正确的手动证明。

外围智能合约的代码审查(在开发过程中)

审计小组还承诺对uniswa -v2-periphery仓库中的智能合约进行一般代码审查和安全分析。

在此过程中开发了另一测试套件，包括使用dapp测试框架的基于属性的模糊测试。这些测试针对的是如今已过时的外围合约版本。

这项工作是在尽最大努力的基础上进行的，外围的变化速度和活跃开发状态意味着审查只在粗略的水平上进行。

团队建议在上线前对最终版本的外围合约进行更多的分析和审查。

在路由中发现了一个中风险的问题:

Router:不兼容代币转账手续费

团队

团队包括klab(一种交互式的证明浏览器和验证工具链)和act(一种面向智能合约的有能力的正式规范语言)的作者。团队还负责MakerDAO的智能合约开发和正式验证:最终完成了多担保Dai的实施和正式验证。

David CurrinDavid TerryDenis ErfurtLev LivnevLorenzo ManacordaMartin Lundfall

发现

提议

类型

安全级别

可能级别

确认情况

提交版本

Router:不兼容代币转账手续费

漏洞

中

高

已确认

Pair:固定流动性通缩引入竞态条件

漏洞

中

中

已确认

uniswap-v2-core@cbe801b

Math:sqrt中的整数溢出

漏洞

低

低

已确认

uniswap-v2-core@d1c8612

ERC20: 构建name,decimals,symbol常量

优化

-

-

已确认

uniswap-v2-core@cbe801b

ERC20: 移除forfeit

优化

-

-

已确认

uniswap-v2-core@cbe801b

Factory: 检索Pair字节码时使用.creationCode

优化

-

-

已确认

uniswap-v2-core@f2d4021

Pair: 用时间戳替换区块高度

优化

-

-

已确认

uniswap-v2-core@a55aa4b

Factory: 用计数器替换allPairs数组

优化

-

-

未确认

Meta: 用继承合约替换math库

优化

-

-

未确认

Pair: 在burn过程中除以0

优化

-

-

未确认

漏洞

Router:不兼容代币转账手续费

为了执行一个铸造，交换或销毁，用户对着合约UniswapV2Router01.sol计算用户需要向UniswapV2Pair.sol传输的数量。

在处理代币减去transferFrom手续费的情况下，UniswapV2Pair接收到的金额小于执行成功交换所需的金额，导致当在交换结束时检查费用调整恒量时使整个调用失败。

这只是router的一个问题，可以使用另外router或代币包装器来缓解这个问题。

Pair:固定流动性通缩引入竞态条件

Dan Robinson发现了一个途径，通过这个途径，早期的流动资金提供者可以使其他流动资金提供者进入的成本非常高，从而使他们垄断流动资金池：

1.在池中有任何流动性之前，攻击者发送少量的Pair双方的代币，接收少量的流动性池股份(“LP代币”)。

2.然后，它们向合约发送大量Pair代币，并调用sync。

这通缩LP代币，使其价值大量Pair代币，这可能会增加其他流动性提供者的进入壁垒，以至于提交足够多的代币以产生1个单位的LP代币，这可能要花费数百万美元。

Uniswap团队建议对此问题进行修复，即强制LP代币的最低供应量为10,000个单位，在mint和burn都实施这一限制。原因是，这将确保流动性代币允许有足够的粒度，即使在有人试图增加进入壁垒之后也是如此。

然而，这一修复带来了另一个问题，恶意的流动性提供者可能牺牲1wei的LP令牌来有效地使合约的最后9999个LP代币不可赎回。换句话说，建议的解决方案可能会使流动性提供者无法退出合约，无法赎回其原始的流动性和费用。

经过与Uniswap团队的讨论，最后确定了另一个解决办法:

当为合约提供初始流动性时(例如，当mint中的totalSupply为0时)，流动性提供者必须牺牲1000个LP代币(通过将它们发送到address(0))。

这在两种方式缓解问题:

LP代币的粒度始终至少为1000执行LP通胀攻击的成本显著增加，因为攻击者现在不是LP代币的唯一持有者。

这种缓解是以为初始流动性提供者引入额外成本为代价的，但预期该成本将足够低，足以令大多数代币接受。对于每个最小面值都具有合理价值的代币，1000wei的经济价值不会超过一个适度的值。然而请注意，在极端情况下一Pair两种代币每wei的价值都在1美元左右，初始流动性提供者的前期成本将在2000美元左右。

Math:sqrt中的整数溢出

Math库合约的sqrt函数实现了计算整数y的平方根的巴比伦方法，即最大整数z，使z^2 <= y。在uniswap-v2-core@d1c8612e之前，迭代的初值为x = (y + 1) / 2，当y = uint(-1)时出现整数溢出，设x为0，导致x_(n + 1)的计算除0。

这不会导致不正确的sqrt返回值，但会导致函数不必要地回滚。我们建议将初始值更改为x = y / 2 + 1，从而使sqrt在其整个域上有很好的定义。

这里给出了该算法的人工正确性证明。

优化

ERC20: 构建 name, decimals, symbol 常量

UniswapV2ERC20合约的name, decimals和symbol 属性是在构造函数中动态设置的。但是，它们总是被继承的UniswapV2Pair合约设置为相同的值，导致不必要的字节码复杂性和gas燃料消耗。

审计团队建议，要么为每一Pair设置唯一的名称和符号，要么在UniswapV2ERC20合约中将这些属性设置为硬编码常量。

基于以下因素，Uniswap团队决定使这些属性保持不变:

Solidity的字符串操作既麻烦又容易出错Uniswap V1交易所都有相同的名称和符号，在自然条件下没有观察到重大问题

这个更改是在uniswap-v2-core@cbe801b5中实现的。

ERC20: 移除 forfeit

UniswapV2ERC20的forfeit方法允许任何人销毁他们的流动性代币，而不会从池中收到代币作为回报。它有效地发挥了对池中所有其他成员的捐赠作用。

虽然在某些情况下，向资金池提供这样的捐赠是可行的(例如，Synthetix使用代币通货膨胀奖励来激励Uniswap V1交易所的流动性提供者)，但同样的结果也可以通过将代币转移给这Pair组合并调用sync来迫使储备与余额匹配来实现。

为了尽量减少核心的UniswapV2Pair合约中允许的状态转换的数量，审计小组因此建议取消 forfeit 和forfeitFrom 方法。

Uniswap团队在uniswaap -v2-core@cbe801b5中接受了这一建议。

Factory: 检索Pair字节码时使用 .creationCode

UniswapV2Factory的createPair方法在构造期间将一Pair字节码存储为raw字节值。当部署一对新的Pair时，字节码必须逐字逐句地从存储器加载到内存中。审计团队建议删除这个存储变量，并将其替换为UniswapV2Pair合约的. creationcode属性，从而简化了代码并清晰意图。在创建Pair时，将字节码从存储中移出还可以显著地节省大量的gas燃料(数百万的gas燃料)，这是由于减少了所需的昂贵的SLOAD操作的数量。

Uniswap团队在Uniswap -v2-core@f2d40214中接受了这一建议。

Pair: 用时间戳替换区块高度

UniswapV2Pair使用价格更新之间经过的块数来计算块加权累积价格。虽然有一些正当的论点认为块高度是比块时间戳更“客观”的变量，但审计团队建议将其更改为使用经过的时间，该时间戳是根据上次价格更新以来块时间戳的变化来度量的。

对于那些不太频繁地对这对价格累加器进行取样的消费者来说，比如那些试图计算几周或几个月时间内的时间加权平均价格的预言机，选择使用块加权或时间戳加权可能会导致重大差异。因此，使用块加权可能会为针对时间加权平均值的预言机带来意想不到的结果(至少在区块链设置之外，这是一个更有经济意义的数字)。

举个具体的例子:在“难度**”硬分叉出现之前的几周内，以太坊的平均阻塞时间会比通常水平增加一倍。块加权价格累加器可能会导致具有较长平均窗口的预言价格与由其他非链源计算的时间加权平均价格显著偏离。为了避免不必要地向用户暴露这些与实现相关的怪异模式，最好使用简单的时间加权。

Factory: 用计数器替换 allPairs 数组

Factory中的allPair数组主要用于维护所有创建的Pair的计数，审计团队注意到它可以被一个简单的计数器所代替。Uniswap团队决定保留数组实现，以防可能需要对数组进行遍历。他们还受审计团队建议，在allPair数组上遍历的任何代码都应该分页，或者以其他方式将访问分解为常量-gas分段，此外，从外部合约变量数组将非常昂贵，需要对每个读取的元素进行一次调用。

由于Soliditty使用插槽的散列作为存储数组的起始位置，因此它们在数组大小整数溢出之前的最大长度取决于它们所在的槽号:maxUInt256 - keccak(uint256(slot)) + 1。

为了完整性，并且由于溢出行为依赖于在源代码中声明变量的顺序是一种不寻常的属性，我们注意到，这种可靠性并不能防止allPairs的(忽略不计的概率)溢出。

Meta: 用继承合约替换Math库

UniswapV2Pair合约依赖于三个库，UQ112x112、SafeMath和Math，它们为uint256安全运算提供了额外的internal函数和定制语法。将这些内部方法直接包含在UniswapV2Pair中(或者从另一个合约中继承)，反而会使创建新pair的成本降低15000 gas燃料。

由于这一更改将不可能利用uint256安全运算的自定义语法，Uniswap团队决定不执行这一建议。

Pair: 在burn过程中除以0

如果在totalSupply为0时调用burn，那么在计算要返回给调用方的金额时，调用将失败，因为要除以0。

当遇到除0时，通过执行INVALID的操作码，Solidity“抛出异常”，消耗初始化调用中的所有gas燃料(不同于REVERT)，如果burn在任何LP股份生成前被意外调用将导致不必要的资金损失。此外，这种在Solidity除0的行为可能不太为人所知，因为它与其他语言(如EVM，其中DIV除0返回0)不同。

此外，一些分析工具将INVALID操作码视为违反断言的行为，而在这里，它更类似于未满足的前置条件。这可能导致错误报告，或者使用这些工具使Uniswap合约的分析复杂化。

由于除零是在那种有限的情况下发生的，其影响也是有限的，审计小组提出它只是为了提供信息目的，因而Uniswap团队没有作任何修改。

设计注释

抢先交易和交易重排

能够影响一个块中包含交易的顺序的参与者可以影响交易的经济结果。审计小组意识到利用这种现象获利的两种策略。这种策略不仅适用于矿工，也适用于任何能够观察未经确认的交易并以仔细挑选的gas燃料价格提交自己交易的那一方。router包含一些特性，这些特性提供了针对第一种策略的某种程度的保护，但是对于第二种策略则不存在这种保护。

这些问题是众所周知的，并且也出现在Uniswap V1中。交易重排和抢先攻击可以被认为是许多使用链上清算和结算的交易场所固有的更广泛的结构性问题。正如在Daian等人的文章中所广泛写到的那样，这种策略在以太坊已经广泛使用了许多年，并且从交易重排特权(矿工可提取价值)中获取挖矿租金甚至会对区块链共识层的安全性造成威胁。

使市场对交易者不利

在这个变形中，可以观察未经确认交易的参与者可以尝试在目标交易之前和之后插入交易，以某种方式操纵交易Pair的价格，这将为抢先者带来利润，而为交易者带来更差的价格。

以ETH/DAI为例。假设一个交易者发送一个交易卖出1ETH。如果抢先者能够在两个分别买卖的交易者间插入交易，很清楚当交易执行完成Pair的状态导致给交易者更低的ETH价格，因为抢先者的卖出，而价格恶化的程度将取决于抢先者第一笔交易的规模（鉴于常数乘积恒量，可以证明该关系是二次方的）。在目标交易执行后，抢先者的第二笔交易执行，买回足够数量的ETH，使这Pair股份的价格回到最初的水平。

遵循平衡的流动,我们观察到插入交易的总经济效应相当于抢先者和交易者之间的交易(流动池最终回到他们初始的位置，只从3个交易中收取了费用)。然而，抢先者能够通过控制第一笔交易的规模来有效地影响交易发生的价格，因此能够任意设定有利于自己的价格。看到的是这仍然使LP手续费有利可图，明显可看到抢先者对应插入交易规模所支付的LP手续费，插入交易在Pair上的价格影响是插入交易规模的二次方，意味着插入交易可以通过足够大的操纵交易获利，而交易者的损失仅受其交易价值的限制。

类似的方法也可以用来攻击进入资金池的流动提供者。

UniswapV2Router01合约上公开的方法包含一些参数，这些参数允许调用方对其订单施加链下滑动限制(AmountOutMin、AmountOutMax)，当适当地设置这些参数时，可以将损失限制在交易者的抢先操作上。但请注意，用这种技术可能不可能完全消除抢先交易，因为将滑动限制设置得太紧可能会导致较低成功率，使市场对交易者不利。

在mint合burn中插入大量交易

在第二种变形中，攻击者监视大型交易，并将目标交易插入与初始池大小相关的非常大的仓位中去调用mint和burn。因此，攻击者能够从该交易的LP手续费中抽取相当大的比例，而不会让自己承担在Uniswap上提供流动性所固有的价格风险。核心合约和外围合约都不包含针对这种攻击的防护，审计团队未发现任何直接有效的解决方案。在核心层对流动性提供者施加最小锁定时间，可能有助于减少与这种攻击相关的利润。

流动性提供者应监控他们参与的Pair交易的活动，以评估这里活动爆发情况，因为这可能导致回报减少。

预言机完整性

尽管AMM(自动做市商)系统，如Uniswap协议，通过其自动价格发现机制，似乎提供了一个令人信服的方式来构建一个信任最小化的链上价格预言机，但事实证明，安全实现这一点并非易事。例如，在大多数实际情况下，简单地从智能合约中查询一个Pair的当前价格这种天真的方法是不安全的，因为价格操纵的成本通常比处于危险中的价值要低。更糟糕的是，通过事后同步执行“反操纵”交易，攻击者通常可以收回大部分操纵成本:有关这类预言机攻击的实际讨论，请参阅samczsun的文章。

因此，在V1 Uniswap协议上构建一个安全的预言价格是非常重要的。所以，V2协议引入了时间加权平均价格累加器:price0CumulativeLast, price1CumulativeLast。累加器在每个块的末尾跟踪Pair累积时间-价格。在两个时间点对累加器进行采样，取其差值，然后除以经过的时间，得到在该时间间隔内块Pair两端的时间加权平均价格。从稳健性的角度来看，这与瞬时价格有两个关键的区别:

平均价格取决于过去出现的价格，与它们出现的时间成比例，预言机用户可以选择平均时间的长度。平均价格不受区块内出现的价格影响，只受区块末的最终价格的影响。特别是，平均价格不受多个交易同步执行时产生的价格影响。

第一点意味着，为了操纵一个使用更长的平均周期的预言机，攻击者需要在更长的时间内维持一个被操纵的价格。第二种方法意味着，攻击者必须在一个区块的末尾维持被操纵的价格，以便对平均值产生影响，这有望通过降低攻击者“解除操纵”价格的可能性，从而使攻击者的成本最大化。

作为一个参考示例，名为ExampleOracleSimple的合约每小时最多对一个Pair的累加器进行采样。因此,为了操纵这预言机提供的价格高于或低于真实的市场价格,攻击者将不得不创建一个情况为可用价格在一个Uniswap的Pair在开始阶段许多区块一个小时期间明显高于或低于市场价格。

给出大多数情况下,攻击者就不会保证收回成本的“反操控”,这个操控的成本可以通过在一段时间考虑所需的交易规模去移动价格至一个给定的水平(如池大小的函数)和区块数量来粗略评估。这种分析的可能起点可以是Angeris等人的计算。在进行这项分析时，应该考虑到一些技术和经济上的细微差别，包括但不限于:

预言机使用者应该检查预言机最近是否更新过(如果没有更新，则调用update())，以避免读取过时的数据基本成本估算没有考虑到流动资金的影响。也就是说，在几个区块的时间框架内，可供套利者使用的链上资本很可能是有限的。例如，攻击者可以操纵价格，等待一个或多个区块的传递，然后通过执行回滚交易来补偿他们的一些初始操纵成本。这将对时间加权平均价格产生影响，但成本可能低于天真的估计。基本成本估算没有考虑网络拥塞和网络交易成本的影响。与流动性效应类似，网络拥塞和成本会降低竞争套利交易的吞吐量，同样也会降低操纵成本。这种分析没有考虑攻击者有能力挖掘或审查区块的可能性。能够审查或操作区块的攻击者可以优先处理自己的交易，并以低得多的成本执行操作。举个具体的例子，矿工可以尝试一种自私的采矿风格的攻击，他们的目标是连续开采两个或更多的区块，然后把它们展示给网络:在这些区块中，它们可能包括使价格被操纵到极值的交易，这些交易可能大到对时间加权平均价格产生有意义的影响，即使操纵发生在少数区块。在最坏的情况下，协议内攻击成本可能仅限于对操纵交易规模征收的LP费用(除了挖掘区块的外部成本等)。

交换可组合性

与使用Uniswap Pair作为价格预言机类似，聪明的合约开发人员可能会发现依赖Uniswap Pair得到链上流动性非常方便。例如，销售加密猫的合约可能提出接受任何代币的付款，立即通过相应的Uniswap Pair将销售的所有收益转换成DAI。类似地，对某些交互收取手续费的合约可能会选择接受多个资产的费用，前提是这些资产可以在支付后交换成DAI。

由于综合了上面的“预言机完整性”设计注释和前面报告提到的交易排序问题，应该小心地设计这种集成，以防止资金损失。特别是,如果所得交换不是针对外部参考价格可靠的检查,然后合约执行交易实际上是依赖于Pair当前的价格作为预言价格,在某种程度上，攻击者可以利用上面概述的交换“插入交易”技术的原子变换来获利。更糟糕的是，对设计错误的合约的攻击实际上比插入交易攻击更容易执行，因为原子性意味着几乎没有执行风险，操作可以完全由链上的“闪电贷”提供资金。

对于这个问题，最好的缓解方法是让交换消费者根据一个可靠的价格参考来检查交易的价格。

时间戳和累加器溢出

涉及缓存的时间戳(blockTimestampLast)和价格累加器(price0collectivativelast、price1collectivativelast)的计算不使用安全数学运算，其设计目的是在溢出时回滚。

在时间戳的情况下，这是一种性能优化，允许将时间戳作为uint32存储在一个存储槽中，与两个保留一起，在每次调用_update时节省两个SSTORE操作。时间戳将每136年溢出一次，下一个溢出点发生在2106年。

在使用累加器的情况下，它是一种安全措施:溢出时的回滚可能导致活性失败(_update中的回滚将阻止交易和LP进入退出)。

尽管溢出的风险非常小，所以它不是18位小数代币的Pair所关注的问题，但是它可以成为一个混合精度代币Pair的实际问题。

我们可以找到一个近似的时间，直到溢出一个给定的Pair:

假设给定Pair的储备比率和每代币1wei美元价格比率一样,我们可以解出示例Pair由一个36位小数代币和一个2位小数代币组成，其中2位小数代币的单位值是36位小数代币的100倍：直到超过8个多月溢出：

因此，建立在核心的价格累加器功能上的预言者应该注意，如果价格累加器溢出在所涉及资产现实可能发生，那么他们的预言者就不应该在溢出点报告的价格中引入峰值或不连续价格。

代币行为的期望

UniswapV2Pair合约直接与它的标的池代币进行交互，并因此对这些代币公开的transfer和balanceOf方法的语义做出某些假设。

慎地使这些相互作用具有防御性，与V1合约相比，V2合约的目的在以下情况使用是安全的:

潜在的可重入的代币在transfer无返回的代币

当然，代币仍然有可能违反Uniswap合约所作的假设。虽然对“良好”代币的完整正式描述超出了本报告的范围，但是审计团队意识到以下代币行为可能会导致V2合约出现问题:

转账以外产生余额变化的代币

有些代币可能会改变帐户的余额，即使该帐户没有涉及transfer代币。例如，这些可以用来实现以实物支付的(正的或负的)利息。这种代币的例子是Ampleforth。

这可能不会对uniswapv2对产生预期的经济影响。例如，如果它代币中的余额在通常的交互之外增加，那么盈余的代币可以由任何账号调用skim索取(而且不会像预期的那样，导致多余的代币累积到池中)。如果有人通过向池转账代币来“空投”代币，也会发生相同的情况。为了让代币积累到池中，sync需要与余额更新或转账同步调用。

转账手续费

在路由中对transfer中断假设收取手续费的代币，在交易时将导致回滚。根据它们的实现，它们也可能在核心中启用一个恶意攻击。

交易手续费可以通过两种方式实现:

1.从已记入转账接收方的金额中扣除费用

2.转帐全额并从发送方的余额中扣除费用

审计团队目前不知道有任何流行的代币使用第二种方法，但至少知道PAXG使用第一种方法。

尽管核心能够处理任何一种类型的代币，但这两种方法都与当前在uniswa -v2-periphery中的router实现不兼容。已指出的讨论在 Router:不兼容代币转账手续费。

此外，如果第二种类型的代币对零余额转账收取费用，那么就有可能发生严重的攻击，因为多次调用skim将允许攻击者将池中的所有代币作为费用耗尽。

极端的精度

Pair将它的储备存储为uint112，但是期望标的代币的balanceOf方法返回uint256。因此，如果余额大于uint112(-1)，则负责将余额与储备同步的内部方法(_update)将回滚。这个方法在mint、burn、swap和sync过程中被调用，这意味着112位或更多位的余额将会阻塞这些方法，直到调用了skim以虹吸掉多余的余额。这就限制了代币合约的功能，在这种情况下，余额超过2的112次方是可以实际实现的。

对于一个普通的18位代币，uint112(-1)表示19,807,040,628,566,084,388,385,987,584(1.9×10191.9×1019或19个10次方)的余额，远远超过任何主流代币的总供应量。

但如果在一个uniswapv2 Pair中使用一个有非常大数量小数的代币，则此限制可能会出现问题。审计团队不知道有任何代币在如此高的精确度下广泛使用。

核心/外围分离

Uniswap V2合约在核心合约和外围合约之间引入了一种分离，其中核心合约负责支持流动性提供者，提供时间加权价格反馈和执行核心记账恒量。为支持或保护交易者而设计的特性是通过外围的单独合约实现的，这些合约调用核心合约。

这种分离有几个好处:

直接访问池代币的代码更少减少了关键恒量的审计表面积使正式方法的应用更容易

但是，在与核心进行交互时，必须注意正确地使用“规范的”外围合约，或者正确地实现定制包装器合约。试图在单独的交易中直接将代币转移到核心是不正确的，并可能导致资金损失。

乐观交换

在UniswapV2Pair中的交换中实现增加了提取代币并使用它们的能力，前提是在交易结束时返回或支付代币。在高层次上，这是通过以下一系列行动来实现的:

1.转账请求输出的金额给到接收人

2.如果data参数是非空的，则使用用户提供的calldata调取接收人

3.计算输入

4.检查手续费调整常数乘积恒量

值得注意的是这个序列:

包含对用户提供的帐户的调用，以及用户提供的调用数据在检查是否提供了足够的输入之前，将代币从Pair中转移出去

对不受信任的代码的调用让正式方法的应用陷入挑战(swap的外部调用有更多的讨论)，这意味着swap详尽的正式规范没有生成。因此，审计小组特别注意到swap中可能出现滥用。

我们不知道任何可能导致违反手续费调整常数乘积恒量的状态转换序列作为调用swap的结果，叫作非病态代币。我们的分析概要如下:

安全属性

为了使用swap提取池代币，攻击者必须让Pair处于这样一种状态:在调用结束时，Pair的保留值的乘积小于调用开始时的值。此外，如果未能补偿流动性提供者对其资金的使用，就不可能成功进行swap操作。

具体来说，必须满足以下公式:

这将确保:

不违反常数乘积恒量流动性提供者从输入的交换获得0.3%的价值

余额 vs 储备

应该注意的是，上述不变式是在储备上定义的，而不是在Pair余额上定义的。

这个检查是类似的，但并不完全相同。从语义上讲，储备可以被认为是“最后记录的余额”。这可能会有问题，因为余额可能是uniswapv2对真正关心的事情。

所有修改储备或余额的方法(skim, sync, mint, burn, swap)都确保在调用结束时两者完全匹配。假设有一个非通缩的代币，强制出现分歧的唯一方法是将代币转换成Pair。

因此，我们可以推断出行为良好的代币系统不变式:余额总是大于或等于UniswapV2Pair调用结束时的储备。

假设持有两个超恒量我们也可以做一些(弱)语句针对超过余额的常数乘积恒量行为:虽然有可能余额的产物减少,这些违反有限的储备乘积,在正常的操作中，是否只会通过对核心的不当使用而显现出来（代币转账到原子交易序列之外的池）。

solidity实现的正确性

恒量检查的可靠实现与上述理想恒量在两个重要方面有所不同:

1.算术溢出和数字范围

solidity可靠性实现对无符号整数进行操作，所有计算(下面讨论的输入数量除外)在溢出时回滚。

这对安全性没有影响:恒量检查在其定义的域上是正确的，并且域足够大，活性不会受到威胁。

2.计算的输入

在下溢状态下，输入量的计算不会回滚。相反，负输入被强制为零。这是一个设计决策，以确保核心能够处理代币，在转账时减少发送方的余额(可能作为一些转账费的实现)。审计和Uniswap开发团队都不知道以这种方式实现的任何主流代币。

从语义上说，一个负的输入量意味着:

调用的开始余额少于储备在调用期间，超过amount{0,1}Out的代币从Pair中转账出去

由于负的输入代表了合约的净流出，对它们收取手续费是不合适的，因此他们强制为零(以及相关的零手续费调整术语)并不代表流动资性提供者的损失。

调用结束时的余额将反映任何意外的差额或额外的流出，调用结束时余额的费用调整后的乘积仍必须超过调用开始时储备的乘积。因此，强制执行零不会为恶意调用者提供利用Pair的途径。

攻击者控制的代码执行

出于这种分析的目的，我们假设攻击者能够在执行他们的代码时修改所有的区块链状态，除了Pair中互斥的保护以外。

这意味着在执行回调期间，以下状态转换不可用:

skimsyncmintburnswap

因此，恶意程式码无法执行:

修改储备mint 或 burn LP 股份从Pair中转账池的代币

应该注意的是，以上Pair的所有方法都不受重入锁的保护。可重入调用到各种LP共享ERC20方法approve, transfer, transferFrom, permit)是可以的。这些方法不修改对恒量检查重要的状态。

审计团队认为，这些限制足以确保攻击者不能使用重入来破坏手续费调整恒量检查:计算的所有输入要么在调用开始时固定(输出数量)，要么受到互斥锁的保护(储备、余额)。

数值误差分析

可能存在数值误差的位置

舍入误差只有在使用平层分割时才会发生。当使用sqrt时，可能还会出现数值错误。根据/和uqdiv提供的平层分割，数值结果(解释为有理数)将小于或等于参数的真实比率(解释为有理数)。对于sqrt，数值结果也保证小于或等于真正的平方根。

在每种情况下，我们使用这个事实来确定任何数值误差的经济影响。我们希望确保的主要特性是:

当进入资金池时，数值误差应始终有利于已经进入资金池的流动性提供者当离开资金池时，数字上的错误应该总是有利于留在资金池内的流动性提供者在与池进行交易时，数字误差应始终有利于流动性提供者当向流动性提供者收取费用时，数字上的错误应该总是有利于流动性提供者

下面，我们列出了每种可能发生数值误差的方法:

_update

在计算价格累加器时存在数值误差，对池本身没有直接的经济影响。累加器数据(如预言机)的使用者应该注意确保错误在其用例的可接受范围内。请注意，如果代币粒度非常低，并且代币余额很低，则舍入的影响可能非常大，无法将该代币有效地用作价格预言。

_mintFee

有两个平方根计算，用于计算自上次调用_mintFee以来k恒量的变化。原则上，这可能导致流动性提供者被收取比他们“理论上”应该收取的费用略高的费用，如果第二个sqrt计算碰巧比第一个有更大的误差。但是，这在经济上并不重要，因为误差很小，而且最重要的是，误差不会累积，并且是有时间限制的。

此外，还存在针对费用接收方(即有利于现有流动性提供者)的分歧。

mint

sqrt用于将初始LP代币供应设置为初始供应代币数量的几何平均值。在这种情况下，数值上的误差似乎不会产生任何经济上的影响，尤其是在减少最低供应量的情况下。

在计算要授予池的新参与者的LP代币数量时，存在一个除法。这里可能出现的错误有利于池中现有的流动性提供者。

burn

当计算要返回给离开池的用户的代币数量时，存在除法。可能的错误是对使用者不利的，即对仍留在池内的流动性提供者有利。

swap

在交换中没有可能引入数字错误的操作。用户可以同时选择数量和合约，而不是计算要支付的金额来交换接收到的数量(或反之亦然)，而合约只是检查结果是常数乘积恒量增加了所需的数量。这将潜在的舍入错误推给调用者，确保数值错误不会导致恒量被违反。

sqrt正确性证明

下面我们证明sqrt将终止在255循环迭代,当使用任何输入从0到2的256次方减1(实际的最大数量的循环迭代似乎是135次),返回值z是最大的整数,z ^ 2 < = y,即 z是y根号四舍五入到最接近的整数。

在处理截断除法时必须注意，这是与标准证明的唯一区别:让div(x,y)表示x除以y的整数结果，没有余数。给定一个大于3的整数y，定义正整数序列(z下标n)为:

对于所有其他n:

很明显，这个序列在某些z下标N处是稳定的，因为它的尾部是一个单调递减的正整数序列。此外，每当z下标n>y根号，我们有z下标n+1<z下标n，因为:

由此可知，极限必须满足z下标N≤y的根号。

很明显，这个序列精确地在sqrt中模拟了计算(我们已经证明了它的终止)，极限是返回值，并且N循环运行的迭代次数。

很容易看出N≤y?y的根号。我们可以加强这一个更有用的绑定定义误差序列?下标n=z的下标n?y的根号,和证明?下标n < 2的负n次方?1得到n < N(证明本质上是一样的无限精确设置)。因此,正如?下标1≤2的255次方,我们可以得出结论,所有输入y < 2的256次方得出的是N<255。

只剩下最后的误差y的根号 - z下标N。为此,我们定义的整数序列r下标n, y =z下标n?div (y,z下标n)+r下标n,所以0≤r下标n<z下标n对于每个n,以及分解z下标N作为总和:

根据AM-GM不等式，第一项严格大于y的根号。第二项严格小于1，因为r下标N?1<z下标N?1。这证明?下标N < 1,或者换句话说,结果z是最大的整数z ^ 2 < = y。

正式验证

在过去，Solidity编译器已经为合约引入了漏洞，将来可能还会这样做。在可能的情况下，手工编写字节码非常困难，而且容易出错。在没有经过验证的编译器的情况下，对代码预期行为的正式规范和对产生的字节码进行验证，可以在某些方面对安全性提出强有力的要求，这些都不包括在非正式的代码评审和常规测试中。

uniswa -v2-core合约的正式规范是用act规范语言编写的。这些规范用K语言编译成可读性声明，并使用K框架验证器针对uniswa -v2-core仓库中构建系统生成的字节码进行验证。

act规范对系统中(几乎)每一种可能的状态转换进行了严格的数学描述。种描述的生成需要在字节码级别上仔细检查合约的运行时行为。规范及其创建过程都为更高层次的推理提供了有价值的基础。

规范可以在dap org/k-uniswap-v2 git仓库中找到。这些规范的证明状态可以在审计组的CI系统dapp.ci/k-uniswap中看到。

警告和假设

合约级别恒量

书面规范定义了对合约方法的单个调用的调用函数行为(函数规范)。从本质上讲，它们并没有声明应该跨多个调用的恒量(合约级别恒量)，例如xy=k常数乘积恒量(或其费用调整后的副本)。

团队认为，规范原则上可以扩展到在合约级别上提出关于恒量的要求(请参阅此处了解更多细节)，但是由于时间限制，这类要求没有作为此合约的一部分进行处理。

代币实现

UniswapV2Pair调用不受信任的外部合约来获取代币余额(balanceOf)并进行代币转账(transfer)。些调用可以导致任何行为，为了简化证明工作，一个语义上匹配uniswap-v2-core/contracts/UniswapV2ERC20.sol中的代币实现已经被假定了。

已知证明声明仅在此上下文中有效，为了对代币可能在语义上偏离此假设的个别Pair的属性进行正式声明，必须为该代币生成一组新的证明。

应该注意的是，恶意代币可能会没收或销毁包含该特定代币的Pair储备。这种攻击的范围仅限于恶意代币是该Pair中的两个代币之一。损失将落在这个Pair组合的流动性提供者身上，因此，流动性提供者应该在提供资金之前仔细审计他们所参与的每个Pair组合的代币实现。

sqrt实现

对于迭代或递归数值算法的正式验证实现，既有理论上的挑战，也有实践上的挑战。要验证sqrt实现的正确性，必须在固定精度设置下检查数值误差和收敛性，同时还要证明收敛性和终止性。因此，生成sqrt的完整的字节码级证明将是困难和耗时的。

由于时间的限制，其实施尚未得到正式的核查。相反，在依赖于sqrt结果的证明中，使用了一个正式的符号表达式，这意味着规范仅断言存储已被调用sqrt的结果更新，但不声明该结果是什么。注意，这还假设计算总是终止，假设提供了足够的gas燃料。

特别关注sqrt的实现，包括模糊测试、手动检查和在固定精度设置下手动验证所选算法的正确性。团队发现了一个微妙的溢出问题。在这个问题得到解决之后，团队确信这个实现适合于使用。

swap外部调用

如果swap的调用者提供一个非空字节数组作为data参数，那么对用户提供的地址的将从Pair调用作为swap执行的一部分。

对未知代码的调用对K验证程序构成了重大挑战。如果不知道调用目标的字节码，验证程序就无法继续符号执行，也就无法推断区块链的状态。实际上，正式地说，我们必须假设所有区块链状态都可以通过对未知代码的调用以某种方式进行修改。因此，在这样一个调用之后对区块链状态进行正式的声明是非常具有挑战性的，而且据团队所知，包含对未知代码的调用的以太坊智能合约的完整正式验证从未完成。

团队认为，UniswapV2Pair中存在的可重入互斥量与一些自定义引线相结合，应该允许生成这样的证明(参见对未知代码的外部调用的验证)，但是时间限制意味着它不是这个约定的一部分。

团队已经仔细注意，并投入大量时间考虑该设施的潜在滥用，并且不知道任何情况下，其使用可能导致违反手续费调整的恒定乘积恒量，禁止病态的代币行为。

重入锁

正式规范只对Uniswap合约中调用开始和结束时的区块链状态进行声明。它们不会在调用期间声明任何状态转换的细节。这意味着重入互斥锁的行为没有完全指定。小组编制了下列证据:

在所有调用的开始和结束时，互斥锁都处于解锁状态如果互斥锁处于锁定状态，则对合约的调用将失败

但是，规范没有对从解锁状态到锁定状态的转换以及在调用中再次转换做出任何声明。

团队密切关注在源代码级别和产生的字节码中互斥锁的实现。此外，还编写并观察了显示重入锁的正确功能的测试。

穷尽性

已经产生了所谓ABI穷尽性的证据，这意味着规范涵盖了合约上的所有方法。但是，目前还没有生成关于完全穷尽性的证明(规范涵盖了所有可能的calldata值的合约行为)。

团队意识到以下未指定行为的实例:

sqrt的实现调用swap的未知代码permit中nonce计数器溢出allPairs数组溢出当token0等于 token1时调用swap当to地址是Pair本身的地址时调用swap当区块时间戳溢出时调用swap当totalSupply等于0时调用burn当调用者是feeTo地址时调用burn当to地址是Pair地址时，当feeTo =/= 0或kLast == 0时，调用burn

在swap情况下，sqrt和对未知代码的调用将在前面的部分中进行讨论。在其余的案例中，做出的决定将不太可能的情况排除在外，以简化规范并将团队的工作集中在被认为是最关键的案例上。

软件栈的可靠性

klab中的一个错误或它的任何依赖项都可能使证明结果无效，或者导致错误的规范被验证器错误地接受。生成的证明的正确性依赖于:

在klab中实现act规范语言K EVM语义K框架定理的验证器Z3 SMT验证器

引理的可靠性

生成证明在许多情况下需要引入各种额外的假设(有时称为引理)。这些假设通常是非常狭窄的技术引理，对于SMT解析器来说是不可行的，但是可以很容易地从数学上证明。尽管团队已经注意记录并证明了这些假设，但是这里的一个错误可能会使任何证明无效。

引理和它们的支持文档可以在k-uniswap-v2/src/lemmas.k.md和k-uniswap-v2 / src / prelude.smt2.md中找到。

Gas燃料

每个方法生成三个证明对象:

pass_roughfail_roughpass

*_rough证明假设该方法是使用非常大量的gas燃料(目前为300000)来执行的。一旦成功地证明了pass_rough规范，在证明中对符号执行的跟踪将用于生成一个符号表达式(G)，表示方法所使用的确切gas燃料(作为状态、calldata等的函数)。然后使用这个gas表达式来生成pass证明，它证明了规范在所有与pass_rough规范相同的条件下，但是进一步加强了它的声明，即所提供的gas燃料量是>= G。

由于K证明程序中的性能限制，如果以gas值< G调用此方法，则无法生成该方法将失败的证明。然而，小组认为这一说法在原则上是可以证明的。

未来工作

审计小组认为，现有的正式规范可以在几个有价值的方向上加以扩展或扩充，并鼓励Uniswap团队今后研究下列问题:

合约级别的恒量

审计团队认为，作为该约定的一部分而生成的act规范可以被扩展，以证明V2 Pair每个可能的调用组合保持核心记录恒量。

小组认为两种可能的方法是可行的:

1.将act规范编译为高级证明语言(如Coq、Agda)

2.在生成的K规范中使用后置条件实现归纳证明

对未知代码的外部调用的验证

团队相信引理的添加重新设置所有可能受到影响的EVM状态，是在调用结束后对抽象值的调用(本质上是不受可重入互斥锁保护的所有状态)允许成功地证明swap中相关代码路径的正确性后。

sqrt字节码的验证

团队相信通过证明sqrt的EVM实现与手工证明收敛的模型一致，应该可以证明循环恒量。

原文链接：https://uniswap.org/audit.html

最后提醒一下，市场有风险，本文只是个研究，不作为投资建议，请合理控制风险。

点赞就是对传教士最大的鼓励，谢谢支持。

—-

编译者/作者：DeFi传教士

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。