当前位置: 玩币族首页 > 新闻观点 > ZKSync中better_better_cs如何实现聚合证明（?）

ZKSync中better_better_cs如何实现聚合证明（?）

2021-06-08 ZKSwap 来源：区块链网络

上篇?章中，我们研读了?ZKSync?中?better_cs?如何?成?single proof、aggregation proof?的电路逻辑等实现。在这篇?章中，我们继续研读?ZKSync?的聚合证明，我们重点关注?better_better_cs?如何?成聚合证明。

还是?上?篇的这张代码调?图，我们这篇着重讲?create_proof。

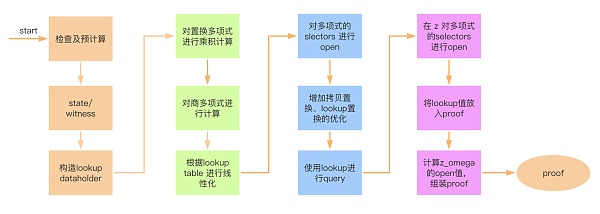
我们分析的?bellman_ce?代码版本是?beta?分?，commit id?为48441155ec7006bf7bfac553b5fb7d466d7fcd00?。

aggregation_proof?的?成create_proof?这个函数在?bellman_ce/src/plonk/better_better_cs/proof/mod.rs?中，将近?2000??代码。

?体上，分为以下?个步骤：

1.?基本的?些检查和预计算// ...

for?idx?in?0..num_state_polys?{

let?key?=?PolyIdentifier::PermutationPolynomial(idx);

let?vals?=?setup.permutation_monomials[idx].clone().fft_using_bitreversed_ntt(

&worker,

&omegas_bitreversed,

&E::Fr::one()

)?.into_coeffs();

let?poly?=?Polynomial::from_values_unpadded(vals)?;

let?poly?=?PolynomialProxy::from_owned(poly);

values_storage.setup_map.insert(key,?poly);

}

2.??成?state?多项式状态和?witness?多项式状态，且为lookup table?参数?成排序好的多项式

// ...

proof.state_polys_commitments.push(commitment);

// ...

proof.witness_polys_commitments.push(commitment);

3.?构造?lookupdataholder，?于后续计算

// ...

let?data?=?data_structures::LookupDataHolder::<E>?{

eta,

f_poly_unpadded_values:?Some(f_poly_values_aggregated),

t_poly_unpadded_values:?Some(t_poly_values),

t_shifted_unpadded_values:?Some(t_poly_values_shifted),

s_poly_unpadded_values:?Some(s_poly_unpadded_values),

s_shifted_unpadded_values:?Some(s_shifted_unpadded_values),

t_poly_monomial:?Some(t_poly_monomial),

s_poly_monomial:?Some(s_poly_monomial),

selector_poly_monomial:?Some(selector_poly),

table_type_poly_monomial:?Some(table_type_mononial),

};

4.?对置换多项式进?乘积（grand product）计算

// ...

let mut?z_2?=?grand_products_proto_it.next().unwrap();

z_2.add_assign_scaled(&worker,?permutation_polys_it.next().unwrap(),

&beta_for_copy_permutation);

for?(mut p,?perm)?in?grand_products_proto_it.zip(permutation_polys_it) {

p.add_assign_scaled(&worker, &perm, &beta_for_copy_permutation);

z_2.mul_assign(&worker, &p);

}

z_2.batch_inversion(&worker)?;

5.?对商多项式进?计算

// ...

let mut?t?=?gate.contribute_into_quotient_for_public_inputs(

required_domain_size,

&input_values,

&mut ldes_storage,

&monomials_storage,

for_gate,

&omegas_bitreversed,

&omegas_inv_bitreversed,

&worker

)?;

// ...

transcript.commit_field_element(&quotient_at_z);

proof.quotient_poly_opening_at_z?=?quotient_at_z;

6.?根据?lookup table?进?线性化

let?queries_with_linearization?=?sort_queries_for_linearization(&self.sorted_gates,

MAX_DILATION);

// ...

for?(dilation_value,?ids)?in

queries_with_linearization.state_polys.iter().enumerate() {...}

for?(dilation_value,?ids)?in

queries_with_linearization.witness_polys.iter().enumerate() {...}

for?(gate_idx,?queries)?in

queries_with_linearization.gate_setup_polys.iter().enumerate() {...}

7.?对多项式的?selectors?进??open?取值

let mut?selector_values?=?vec![];

for?s?in?queries_with_linearization.gate_selectors.iter() {

let?gate_index?=?self.sorted_gates.iter().position(|r|?r?==?s).unwrap();

let?key?=?PolyIdentifier::GateSelector(s.name());

let?poly_ref?=?monomials_storage.gate_selectors.get(&key).unwrap().as_ref();

let?value?=?poly_ref.evaluate_at(&worker,?z);

transcript.commit_field_element(&value);

proof.gate_selectors_openings_at_z.push((gate_index,?value));

selector_values.push(value);

}

8.?增加拷?置换多项式、lookup置换的优化结果// ...

r_poly.add_assign_scaled(&worker, &copy_permutation_z_in_monomial_form, &factor);

r_poly.sub_assign_scaled(&worker,?last_permutation_poly_ref, &factor);

r_poly.add_assign_scaled(&worker, &copy_permutation_z_in_monomial_form, &factor);

9.?使??lookup?进??query

let?query?=?LookupQuery::<E>?{

s_at_z_omega,

grand_product_at_z_omega,

t_at_z,

t_at_z_omega,

selector_at_z,

table_type_at_z,

};

10.?对多项式的?selectors?在?z?进??open?取值

for?s?in?queries_with_linearization.gate_selectors.iter() {

multiopening_challenge.mul_assign(&v);

let?key?=?PolyIdentifier::GateSelector(s.name());

let?poly_ref?=?monomials_storage.get_poly(key);

poly_to_divide_at_z.add_assign_scaled(&worker,?poly_ref,

&multiopening_challenge);

}

11.?将最终的?lookup?值放?proof中

if let?Some(data)?=?lookup_data.as_ref() {

// we need to add t(x), selector(x) and table type(x)

multiopening_challenge.mul_assign(&v);

let?poly_ref?=?data.t_poly_monomial.as_ref().unwrap().as_ref();

poly_to_divide_at_z.add_assign_scaled(&worker,?poly_ref,

&multiopening_challenge);

multiopening_challenge.mul_assign(&v);

let?poly_ref?=?data.selector_poly_monomial.as_ref().unwrap().as_ref();

poly_to_divide_at_z.add_assign_scaled(&worker,?poly_ref,

&multiopening_challenge);

multiopening_challenge.mul_assign(&v);

let?poly_ref?=?data.table_type_poly_monomial.as_ref().unwrap().as_ref();

poly_to_divide_at_z.add_assign_scaled(&worker,?poly_ref,

&multiopening_challenge);

}

12.?计算?z、z_omega?处的?open?值，最后组装?proof?在这个函数中，我们看到了熟悉的?MainGate?函数，从上?版如何实现聚合中，我们知道这个?于?的

设计，可以实现?custom gate，达到优化电路的?的。?除开?custom gate，ZKSync?中还使?了

plonkup（即?plonk + lookup table）来提升效率。

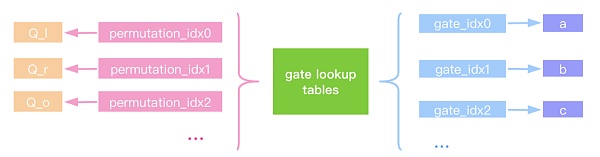
我们在之前的?章中，已经讲解过plonkup的原理了，简单来说，就是预计算有效的input/output组成

lookup table，prover需要证明witness在这个table?，详细内容请参?ZKSwap团队解读Plookup原理。

ZKSync?对?plonkup?的实现，并不是将?custom gate?和?plonkup?分开的，?是结合在?起来优化电路设计的。

我们下?看看，MainGate trait?中的接?，是如何和?plonkup?结合的。

lookup?的使?

在上?节的?create_proof?函数中，线性化?到了?gate?的

contribute_into_linearization_for_public_inputs?函数，我们以它为例，来看看?lookup?的使?。这个代码在?bellman_ce/src/plonk/better_better_cs/cs.rs?中。

let?open_at_z_omega?=?polys.pop().unwrap().0;

let?open_at_z?=?polys.pop().unwrap().0;

let?opening_at_z?=?commit_using_monomials(

&open_at_z,

&mon_crs,

&worker

)?;

let?opening_at_z_omega?=?commit_using_monomials(

&open_at_z_omega,

&mon_crs,

&worker

)?;

proof.opening_proof_at_z?=?opening_at_z;

proof.opening_proof_at_z_omega?=?opening_at_z_omega;fn?contribute_into_linearization_for_public_inputs(

&self,

_domain_size:?usize,

_public_inputs: &[E::Fr],

_at:?E::Fr,

queried_values: &std::collections::HashMap<PolynomialInConstraint,?E::Fr>,

monomials_storage: &?AssembledPolynomialStorageForMonomialForms<E>,

challenges: &[E::Fr],

worker: &Worker

)?->?Result<Polynomial<E::Fr,?Coefficients>,?SynthesisError>?{}

?到的传?参数有?hashmap?格式的?queried_values、单项式缓存值、随机数数组。queried_values?这个参数是在?create_proof?时，根据排序的query?列表?成的，key?是多项式，value是?Fr?值。query?列表的排序规则是先witness、gate?的selector?次之、gate?的setup?再次之，这个?SortedGateQueries?的结构是：

pub struct?SortedGateQueries<E:?Engine>{

pub?state_polys:?Vec<Vec<PolyIdentifier>>,?// state?多项式

pub?witness_polys:?Vec<Vec<PolyIdentifier>>,?// witness?多项式

pub?gate_selectors:?Vec<Box<dyn GateInternal<E>>>,?// gate?的selectors

pub?gate_setup_polys:?Vec<Vec<Vec<PolyIdentifier>>>,?// gate setup?多项式

}

代码中，调??sort_queries_for_linearization?函数来?成?SortedGateQueries?，这个函数也在当

前?mod.rs??件中。这个函数输?参数是?gate?数组，输出即为?SortedGateQueries?。

fn?sort_queries_for_linearization<E:?Engine>(gates: &?Vec<Box<dyn GateInternal<E>>>,

max_dilation:?usize)

->?SortedGateQueries<E>?{

}

函数会对传?的?gate?数组遍历，根据gate返回的多项式数组，将其按照?VariablesPolynomial?，

WitnessPolynomial?，?GateSetupPolynomial?的不同类型，将多项式存??SortedGateQueries?中。

回到?contribute_into_linearization_for_public_inputs?函数，可以看到，它会从queried_values

中，获取?a/b/c/d?的值。??Q_a/Q_b/Q_c/Q_d/Q_m的值，都是从?create_proof?刚开始?成的单项式缓存数据中取到的，也是?个lookup table?的概念

这个单项式缓存的值是从电路的setup?获得的，即电路确定了，那么电路的?就确定了，则在?成proof时，这些数据都已经有了，可以直接将setup?预计算的结果，放??lookup table?中，查询使?数据。let mut?monomials_storage?=?Self::create_monomial_storage(

&worker,

&omegas_inv_bitreversed,

&values_storage,

true

)?;

monomials_storage.extend_from_setup(setup)?;

最后，结合a/b/c/d和Q_a/Q_b/Q_c/Q_d，可以?常?便的构造出多项式。

//?可以看到，?常?效的get取到了数据

let?a_value?=

*queried_values.get(&PolynomialInConstraint::from_id(PolyIdentifier::VariablesPolynomia

l(0)))