引言 在一堆不同的项目中,我们需要允许用户从 EVM 存入某种链下状态,该状态在链上表示为 Merkle 累加器(例如 Merkle 树的根)。该 Merkle 树根据有效性证明(例如 SNARK)或欺诈证明+同步假设进行更新。 SNARK友好的哈希函数非常昂贵,因此有必要最小化它的成本。在optimistic rollups世界中,它并不那么昂贵,但每次存款的成本限制了它在某些场景下的应用,例如大规模迁移。 要从EVM存入Merkle树,需要执行tree_depth哈希从而能够包含一个叶子节点。甚至在一个区块中有两笔存款都需要tree_depth的哈希值。那么有必要将它们合并在一起,这样它们只需要花费(tree_depth+1)个哈希值。 这些存款为
,在这里,我们提出了一种存储批处理方法,即
在另一篇文章中,我们将这些优化应用于mixers和optimistic rollups。 之前的工作 Merkle Mountain Ranges专注于创建深度随时间增长的 Merkle 树。在这个使用案例中,我们需要一个恒定深度的树,并且不能有可变数量的哈希值。在optimistic rollup中,这也不理想,因为随着树的深度的增长,需要更改放在链上的数据。 将此用于存储是有问题的,因为随着数据集变大,峰值袋变得越来越稀少,因此存款速度变得越来越慢。这可能导致用户无限期地等待他们的资金存入。 另一种方法是多重证明但在这里不能使用,因为它需要在存款人之间安排协调员。鉴于不断变化的存款队列,状态很可能在协调更新得到处理之前已经改变。 方法 创建存款队列 如果您曾经玩过 2048,您可能会从合并两个相同值的区块中获得乐趣。我们在这里对于 Merkle 树也这么做。 我们从一个空的存款树开始。当存款进来时,我们将其存储在队列中并等待。当下一笔存款进入此哈希时,将此哈希保存到我们当前深度为1、同时有2个待处理存款的存款树。然后我们可以停止存储与第一笔存款相关的任何数据。 当另一笔存款进来时,我们会再次存储它。然后对于下一个存款,我们用指定值对其进行哈希,然后用存款树对结果进行哈希。创建我们的深度为2、有 4 个待处理存款的存款树。 我们已经有效地合并了存款。 将存款树插入余额树中 此时,我们有一个深度为2的存款树(deposit tree),其中有4个待处理的存款。我们还有一个余额树(balance tree),它包含一些先前存入的账户,其他地方都是零。我们不想覆盖树中的帐户。因为这会毁掉这些用户的账户。我们只需要将它们替换0。 为了将新叶子插入余额树,我们需要证明: 一个节点的子节点全为零。我们需要这样做以防止覆盖已经有过存款的账户。 举个例子,假设我们有一个节点有 2 个子节点。我们知道,如果 2 个子节点都是 0,那么节点 == hash(0,0)。 但是如果树真的很深,在 EVM/SNARK 中计算这个哈希可能效率不高。因此,不如预先计算这个列表,并将其作为一个映射存储在智能合约中进行部署。
我们之前已经证明了一片叶子的子节点全为零,现在我们想要改变那片叶子,同时保持树的其余部分不变。 使用相同的 Merkle 路径,我们计算了用 deposit_tree 替换的没有叶子的根。 然后我们将这个新的 Merkle 根存储为包含所有存放叶子的新余额树,使用我们用来证明叶子在树中的相同 Merkle 路径确保了所有其他叶子不会改变,并且只允许我们更新零节点的子节点。
同步的注意事项 像 zksnarks/optimistic rollup 这样的一些系统需要证明时间才能执行存款。如果在这种情况下存款树发生变化,则证明可能无效。因此,最好有一种方法可以在某个存款树被存入时暂停更新。 概括 这里我们提出了一种合并存款的方法。我们在 EVM 中查询存款,当它们被存入更大的Merkle树时,它们会将它们合并。 在后续文章中,我们将把它应用到mixer存款和optimistic rollup存款/大规模迁移。 讨论: weijiekoh 假设队列长度是 8 而不是 4。 令 storage 为存储一个值所需的 gas 量。 令 hash 为哈希两个值所需的 gas 量。
barryWhiteHat 与现状相比,对每个人来说都更便宜? weijiekoh 它确实对每个人来说都更便宜,在我看来,当考虑到每次哈希的成本时,这种权衡是一个偏好问题。如果哈希函数是便宜的(例如kecack),那么成本差异可以忽略不计,但如果哈希函数是昂贵的(例如Poseidon)那么
vbuterin 因此Kate Commitment值得探索。使用 Kate Commitment,只需一个组元素(48-96 字节)就可以轻松证明来自单个状态的任意数量的位置。这可以与队列方法结合使用,以确保有大量存款可以批量处理。Kate 方法的另一个好处是很容易将其插入基于椭圆曲线的 SNARK/PLONK 证明中。 weijiekoh 请问你对使用Kate Commitment有什么想法?是把所有的存款根积累到Kate Commitment而不是余额树的吗? vbuterin 将Kate Commitment使用于存款和余额。 weijiekoh 尽管用我们拥有的最好的开发工具(带circom的BN254)来验证在snark中的Kate Commitment仍然是不可行的。但我的意见是,我们必须等到更先进的snarks变得可行。 vbuterin 我没想过让 snark 从字面上验证椭圆曲线配对计算。我正在考虑使用类似 PLONK 的多项式证明,其中 Kate Commitment和opening作为两个参数传入,您只需直接对它们进行多项式检查。所以没有“一个系统验证另一个系统”的开销。 weijiekoh 请问这是你心目中的 snark 吗?
在这种情况下,像 (在 snark 中的)commit() 函数需要一个 SRS 并且还需要对EC 取幂来计算 Kate 承诺。我可能是错的,但由于在现有的alt_bn128的SRSes 上执行 EC 操作的成本很高,我们是否需要在 BabyJub 曲线上进行新的'Powers of Tau Ceremony',以便我们可以拥有对 snark 友好的 Kate Commitment? MichaelConnor 可以批量处理成 Kate Commitment的项目数量是否有实际上限?限制是 SRS 的大小?如果是这样,Merkle树不是提供更大的匿名集吗? vbuterin 我的意思是直接对Kate Commitment进行多重证明。所以你会有一个承诺P,你只需做一个标准的muti-opening来证明 对于一组 (x,y) 有P(xi)=yi 成立。 可以更进一步:为了避免每对都进行一次EC 乘法, (x,y) 对本身可以用多项式承诺进行编码,muti-opening将变成一个等价证明:(你可以使用标准的 PLONK 技巧来证明它在一定范围内是真的 ),然后这些多项式承诺将同时成为 PLONK 证明的一部分。 weijiekoh [讨论减少模式] 也许我应该从不同的角度去看问题。我主要关心用户的 gas 成本,其次才是协调器。这毕竟是批量存款技术要解决的问题。 在 MACI 中,我们需要证明 ZK 中余额树中每个叶子的事情。即在余额树(也就是 MACI 命名法中的消息树)中,每个叶子可能会或可能不会根据其解密内容修改状态树(例如,消息叶子是一个加密命令,可能会更改用户的公钥)。由于我们要确保协调器以正确的顺序处理每条消息,我们的 Groth16 snark 必须证明每个叶子的成员资格和消息树中的位置。 这已经花费了几十万gas。如果我们执行 Kate 多重证明,将至少添加另外 193k gas(其中大部分用于配对检查预编译)。 如果/当我们转向 PLONK(取决于开发工具),我们是否可以避免这种额外成本? [讨论展开模式] 在短期内,如果没有 PLONK,在 BabyJub 中使用 Kate 承诺可能会有好处,因此我们可以在 Groth16 snark 中验证 Kate 承诺或 Kate verkle 树。 每个存入队列的用户只需支付存储 32 个字节的费用。 一旦存款队列已满,协调员就会累积成一个凯特承诺,这应该很便宜。例如,Kate 提交 16 个值需要 223454 个 gas,这比波塞冬二叉 Merkle 树有很大的改进,后者需要 797835 个 gas 来提交 16 个值。这样,用户和协调者都可以节省 gas。 为了构建最终的余额树,协调器还将使用 Kate 承诺,从而生成 Verkle 树。由于我们可以以更低的 gas 成本承诺更多的价值,我们可以拥有更大的树容量。 当我们处理余额树(又名消息树)时,我们会检查 snark 中每条消息的成员资格和位置,然后照常进行。 也许我们可以使用Verkle树(Merkle树使用Kate承诺作为哈希函数而不是Poseidon/MiMC)。 Pratyush KZG10 Commitments需要配对;BabyJubJub不是一个友好的配对曲线 weijiekoh 使用这种技术可以节省更多的gas。子树的哈希函数可以是SHA256,这在EVM中比较便宜。树的其余部分(从子树深入到根)可以用Poseidon进行哈希。 这样做的代价是,任何 snark 都会增加每个子树级别大约 90k 约束。从这个角度来看,Tornado?Cash的抽屉式电路(withdraw circuit)有28271个约束条件。因此,这种方法只对MACI这样的用例有意义,在这种情况下,验证者可能不介意(粗略地)将他们的验证时间增加一倍甚至三倍。 查看更多 —- 编译者/作者:DAOrayaki_ 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
?DAOrayaki|[op/zk]rollup/mixers/MACI的批量处理存款
2021-12-21 DAOrayaki_ 来源:区块链网络
相关阅读:
- 算稳资产Gyro能否用「收益+用例」打开DeFi2_0的创新下半场2021-12-21
- 加密市场价值开始复苏! 在急剧下跌至 2 万亿美元之后。2021-12-21
- 以太坊宣布“Kintsugi 测试网”准备与 Eth 2.0 的网络集成2021-12-21
- 基于以太坊的流动质押解决方案 Lido 宣布整合 Chainlink Price Feeds2021-12-21
- 首届世界元宇宙大会在元宇宙“WMA元宇宙博览会”上成功召开2021-12-21






 然后每当我们想要检查一个节点的子节点是否全为零时,我们只需查找此映射。所以有用Merkle证明该节点在树中,然后通过检查存储的映射证明它的子节点全为零。新的 Merkle 根只更改了零节点,其他一切都相同。
然后每当我们想要检查一个节点的子节点是否全为零时,我们只需查找此映射。所以有用Merkle证明该节点在树中,然后通过检查存储的映射证明它的子节点全为零。新的 Merkle 根只更改了零节点,其他一切都相同。
 这是否意味着存储在2^n位置用户由于其在队列中的位置而处于劣势。
这是否意味着存储在2^n位置用户由于其在队列中的位置而处于劣势。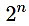 的使用者的gas花费加起来也比较昂贵。
的使用者的gas花费加起来也比较昂贵。

