门限 ECDSA——更安全、更私密的多重签名

Antonio Salazar Cardozo 文?文

本文由币信研究院原创编译，原文链接:

https://blog.keep.network/threshold-ecdsa-safer-more-private-multi-signatures-51153f3e9ed2

本文版权归原作者所有，仅代表作者本人观点，不代表币信或币信研究院的观点或立场。

本文约 6800 字，阅读全文需约 20 分钟。

Keep 开发者 Piotr?Dyraga?在 2018 年旧金山区块链周上关于门限 ECDSA 的演讲

2018年10月9日，在旧金山区块链周的 Epicenter 会议上，Keep 的 Piotr Dyraga 就门限椭圆曲线数字签名算法（t- ECDSA）进行了演讲。

去年夏天，Piotr 和他的代码合作伙伴 Jakub Nowakowski?为Keep实现了一个原型门限 ECDSA 协议（并在比特币测试网上创建了一笔门限 ECDSA 签名的交易！），Piotr 上台展示了该技术解锁的一些可能性，以及有关其如何在底层运作的一些技术细节。

……

首先，我们将讨论多重签名（multi-signatures）——它们是什么，它们在比特币中的运作方式，以及它们在以太坊中的运作方式。然后，我们将讨论门限签名（threshold signatures）及其与多重签名相比的优缺点。最后——事情会变得有些疯狂——我们将探讨一些密码学的东西，并讨论门限 ECDSA 协议——类似于 Keep 中的实现方式。

在继续进行之前，请允许我告诉你一些有关 Keep 的信息，因为这将有助于更好地理解为什么我们开始有关门限签名的工作。如果仅用一句话来描述 Keep，我会说Keep是公链的隐私层。

在过去的几年中，公链为我们带来了令人难以置信的透明性和可审计性（auditability），以及抗审查和不可篡改的记录。但是，竞争利益可以轻松访问发布到区块链的任何智能合约。结果，当公司考虑在区块链上构建应用时，隐私是出现的主要问题之一。Keep 是公链和隐私之间的桥梁，允许合约利用区块链技术的全部功能而不会损害安全性。我们也可以说，Keep 是一种私人计算机，能够存储和处理甚至隐藏在自身之外的数据。

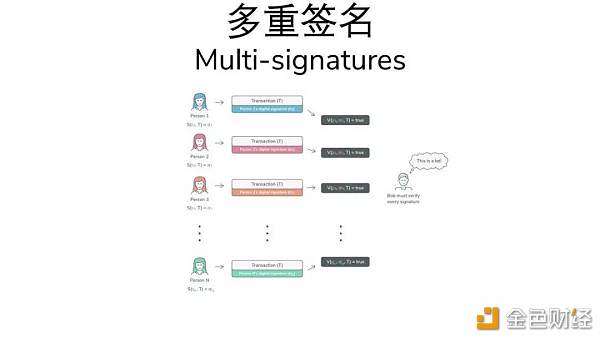
让我们从多重签名开始。“多重签名”通常是指需要多把密钥来签署交易，并且通常被用于划分责任。

1-2 多重签名的一个很好的例子，是夫妻的小额现金联名账户，其中任何一方的签名都足以执行交易。

2-2 多重签名的一个例子，是夫妻双方的储蓄帐户，需要双方同意才能执行交易。

2-3 多重签名的一个例子，是父母对孩子的储蓄帐户。孩子可以在至少一位父母的同意下花钱，如果父母双方都同意，钱可以完全从孩子那里拿走。

在比特币中，多重签名通过创建一个多重签名地址来运作，并且在创建多重签名地址时，我们指定与该地址关联的密钥以及签署交易需要多少把密钥。然后，经过一段时间，我们创建了一个交易，有人用密钥对其进行签名，就是这样！在此案例中，我们创建了具有三把关联密钥的多重签名地址，并且至少需要两把密钥才能提供签名。

这确实很酷，但也有一些限制。

首先，使用哪把密钥来履行交易的信息是公开的。对于某些企业来说，这可能是一种优点，但是对于其他一些需要更大匿名性的企业来说，则可能是一种缺点。另外，在可以使用多少把密钥上也有一些限制。一旦创建了多重签名地址，安全策略就固定下来了。因此，你不能在一段时间之后改变主意，说：“好吧，现在我要使用 2-3 的策略，而不是 5-6 的策略”，它需要创建一个有着新安全政策的新多重签名地址，并把所有资金转移过去。

它在以太坊中的运作方式有些不同，因为这里没有像多重签名这样的东西。总有一个地址来签署一笔交易并花费 gas。但是，有一些多重签名钱包，它们基本上是智能合约，能够存储代币并且要求发起的交易需要接受某些要求，包括特定的签名配置。

最著名的几个钱包是 BitGo 钱包、Gnosis 钱包和 Parity 钱包。而且，尽管它们是智能合约（所以它们显然要比比特币交易具有更大的灵活性），它们也更难以实现。而且，一旦发生错误，错误的成本也确实很高。我想这里的每个人都听说过 Parity 被黑的故事。

那么，有没有更好的方法？我认为答案是“是”。那就是门限签名。

多重签名机制依赖于拥有单独而唯一的密钥的各方，他们用这些密钥来对一笔交易签名，并且，签名者一个接一个地提供其签名。在（上方）这张图片中，我们在左侧有一组签名者。每个签名者都有自己的密钥，他们用它来签署一笔交易。当验证者 Bob（在右侧）想要验证交易时，他需要分别检查每个签名。

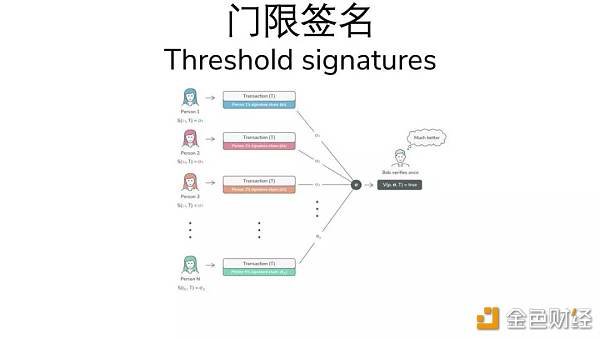
对于门限签名，情况有所不同，因为我们只有一把公钥，一把密钥和一个签名。在上图中，左侧有一组签名者。每个签名者都有相同的公钥和私钥的一个唯一部分。签名者使用一种特殊的通信协议进行协作，该协议不会为了生成签名而暴露密钥，并且只会生成一个签名。现在，验证者只需检查一个签名即可确定交易是否正确。

那么，什么门限签名可以给我们带来什么呢？首先，我们避免了基于合约的多重签名。使用门限签名，我们可以让多方签署以太坊交易，而无需将我们的代币锁定在智能合约钱包中。我认为这对以太坊来说是一个巨大的胜利。其次，门限签名在链上是无法区分的。

这是我们在比特币测试网络上执行的具有 20 个签名者的门限交易示例。你会注意到，这笔交易与只有一个签名者的标准比特币交易之间没有区别。这提供了更大的匿名性，因为有关哪些部分被用于签署交易（即谁签署了交易）的信息不会被公开泄漏。

同样，就验证而言，门限签名比多重签名交易便宜。多重签名需要为每个签名者创建一个新的签名，并且成本随着签名者数量的增加而增加。对于门限签名，只有一个签名，因此在验证方面成本是固定的。

门限签名还提供了更好的灵活性。首先，签名者的数量不限。其次，可以在一段时间后修改安全策略。它是一种单点故障算法，但是你仍然可以改变主意，说：“好吧，我要 3-6 而不是 7-10。”

但是总会有陷阱存在。第一个陷阱是，尽管门限签名并不是什么新鲜事物，但大多数人仍不熟悉它们。这意味着要花一些时间来接受这项技术。而且，工具还不存在。对于多重签名，我们有一堆工具，比如有良好 UI 支持的硬件钱包。在门限签名这里没有这些东西，至少现在还没有。另一个问题是签名者需要保持在线。对于多重签名，你可以提供你的签名，然后下线去度假，同时，其他人过来提供另一个签名，交易就会被接受。对于门限签名，签名者需要合作（至少达到最低数量）才能产生签名。

我希望这一切对你来说都令人兴奋！现在是时候讨论它实际上如何运作了。但首先，我们需要回顾一些模型和定义。它们是“加法同态加密（additively homomorphic encryption）”，“门限加密（threshold encryption）”和“承诺方案（commitment scheme）”。

首先，是加法同态加密。同态加法加密有一个很好的功能，可以对密文进行运算。加法同态加密方案的一个示例是 Pailier，对于该方案，存在一个可有效计算的运算“加”，因此加法运算（在幻灯片上带有 e 分指数）可将两个密文加在一起。

因此，如果我们有两个值 a?和 b。我们可以首先加密这两个值，然后用这一特殊运算将这两个密文加在一起。或者，我们可以首先有这两个值，然后将它们加在一起，然后对结果进行加密。当我们解密时，在两种情况下我们将获得完全相同的值。

接下来是（t，n）门限加密。解释它的最简单方法，是说我们有 n 个参与者；每个人都有相同的公钥，但每个人也都有私钥的独特部分。因此，在这张幻灯片上，我们有 secret_share 1，secret_share 2，secret_share 3 … secret_share n 和签名者——如果你有一条用公钥加密的消息，则签名者必须使用一种特殊通信协议进行合作，这种协议不会为了解密而暴露密钥。

例如，假设 Alice 和 Caroline 正在玩掷硬币游戏。Alice 选择硬币的一面，评估对其选择的承诺，并将承诺发送给 Caroline 。现在， Caroline 将硬币扔向空中，说出结果会是什么。接下来，Alice 发送一个特殊的值，称为解除承诺密钥（decommitment key），它使得 Caroline 可以评估承诺并查看 Alice 最初选的值是否真的如她现在所说。

解除承诺密钥可以验证承诺，但它还有一个很棒的功能，即允许定义无条件的隐藏方案。因此，无论 Caroline 做什么，无论她具有多么高的算力，如果没有解除承诺密钥，她都无法猜测 Alice 承诺的值。她不能仅凭承诺就做到这一点。

现在该讨论协议了。我们的实现基于纽约城市学院和普林斯顿大学的 Rosario Gennaro、Steven Goldfeder 和 Arvind Narayanan 的工作，他们描述了门限最佳 DSA/ECDSA 签名及其在比特币钱包安全中的应用（https://link.springer.com/chapter/10.1007/978-3-319-39555-5_9）。我们对该协议做了一些小的修改，但是现在没有时间讨论它。并且，协议由两个部分组成：密钥生成协议和签名协议。我们将首先讨论密钥生成。

我们现在就要讨论密码学了。假设我们有 n 位签名者，每位签名者都用加法同态门限加密方案进行了初始化，并且这种情况发生在设置阶段：

现在，我们将跳过它是怎样完成的，并在最后回过头来进行简要的讨论。

这可能会造成混淆，因为我们有两种类型的密钥。一种是门限加法同态加密方案密钥（threshold additively homomorphic encryption scheme key），这些密钥在设置阶段已初始化，另一种是我们用于签名的 门限-ECDSA 密钥（t-ECDSA key）。这第二种密钥就是我们现在要生成的。对于加法同态门限加密方案，我们仅假设它是在设置阶段完成的。

在第一步里，每位参与者选择一个随机整数 x，它将被用于该参与者的私钥部分：

x?不能大于 q?。q?是椭圆曲线的基数，因此它是椭圆曲线有的点数。在所有的幻灯片里，q?都代表椭圆曲线的基数。每个参与者将 y?计算为 g?的 x?次幂。这是一种椭圆曲线运算，基本上，我们将曲线的生成点乘以 x?。这是你经常在组里用到的一种表示法，但是由于椭圆曲线是一个组，因此我们也可以在这里使用它。

然后，每个参与者计算对此值的承诺，并在第 2 轮中，将该承诺发布给组里的所有参与者：

接下来，在第三步中，每个参与者都揭示加密形式的?x，在幻灯片上为 α?：

加密是通过我们在设置阶段初始化的加法同态加密方案完成的。此外，每个参与者都揭示公钥部分、解除授权密钥，以及表明所有这些值合在一起正确的零知识证明。这不仅可以验证承诺，还可以让所有参与者查看他们刚刚一起展示的所有部分是否正确。

这样，零知识证明说的是，存在一个数字 x?，于是曲线的生成点的 x 次方等于y?，并且 y?是公开的，因为它刚刚被揭示，并且如果我们解密刚刚发布的值 α?——这是加密的密钥——我们将获得该数字 x?。

当然，这是一个零知识证明，所以我们不可能猜出 x?是多少，但我们在这里说的是，它位于（-q?, q?）的区间内，由于 q?是椭圆曲线的基数，这个范围确实很大。

在第四步中，所有签名者都使用加法同态门限方案的加法运算来生成最终的 t-ECDSA 密钥，因此可以将 x 的所有加密部分相加：

作为结果，我们得到了加密形式的密钥，y 的所有显露出来的公共部分可以被相加，并且，作为结果，我们得到了公钥。这里的加法运算只是椭圆曲线点的加法，因此很简单。

第二部分是签名——让我们看一下签名算法。

我们有了?α，它是所有签名者之间共享的加密形式的 t-ECDSA 私钥，而且我们有了 y，它是 t-ECDSA 公钥；它只是椭圆曲线上的一个点。

在第一轮中，各方都挑一个随机整数 ρ：

使用加法同态门限加密方案对该值进行加密：

并将 ECDSA 密钥（幻灯片上的α）乘以该随机值：

我们能这样做，因为有了加法同态加密方案的加法运算，我们也可以进行乘法。每个签名者都发布对这些值的承诺，并在第二轮中揭示所有这些值以及零知识证明，指出它们是正确的：

在本演示中，我们跳过了零知识证明的构造。

因此，在第二回合之后，参与者使用同态加密方案定义的加法运算，将揭示出的各个部分合并在一起。

第 3 轮和第 4 轮使用相同的承诺-揭示模式：

在右侧，我们具有到目前为止评估的所有参数，并且所有参与者都具有相同的值。

在第三轮中，每一方挑选一个随机整数 k?：

和随机整数 c?：

q?始终代表椭圆曲线的基数，也就是椭圆曲线上的点数。

各方把 r??计算为 g 的 k?次方——我们基本上用它来乘以曲线生成点：

各方计算参数 w?，它是 k?乘以 ρ?加上 c?乘以 q

q?一直是椭圆曲线的基数，由于我们使用加法同态门限加密，因此我们可以对其进行计算。

最后，各方承诺所有这些参数，并在第 4 轮中揭示生成的参数，以及说明它们在一起正确的零知识证明：

现在，我们跳过零知识证明。

有了所有小组成员的所有参数之后，我们可以将它们加在一起，就像在第 2 轮之后一样。我们把所有 k?部分，所有 c?部分，所有 w?部分相加。更重要的是，我们把参数 r?评估为所有 r??部分的总和，我们使用了一种特殊的哈希函数：

实际上，这是我们从标准 ECDSA 协议中知道的函数：它是x?点坐标模除（modulo，译注：一个数除以另一个数的余数）椭圆曲线的阶数；这是来自标准 ECDSA 协议的内容。

在第 4 轮之后，右侧的所有参数将由组里的所有签名者共享。现在我们需要玩一些离散数学的把戏来产生一个签名。使用到目前为止我们评估过的所有这些参数，由于我们运算的是加密的数据，因此签名也会是加密的。但这是我们将在最后的第 6 轮中处理的事情。

我们要做的第一件事是执行门限解密机制，以便使所有参与者都解密参数 w?并把该值赋给 η：

接下来，我们计算一个叫 Ψ?的参数，它是 η?的模 q 乘法逆元，并且 q?一直是椭圆曲线的基数：

然后，有了 m，即我们正在签名的消息的哈希值（或这笔交易的哈希值），我们开始使用以下公式评估签名：?

c?是我们刚刚评估过的值，而 u?，r?和 v?是所有签名者在前几轮中共同评估的参数。

因此，由于 u?是一个加密的 ρ?，并且 v?是一个加密的 ρ?乘以 ECDSA 密钥，因此我们可以执行以下转换：

如果我们把 Ψ?替换为它所代表的值，我们会得到下面的公式：

最后，如果消掉 ρ?，我们得到：

我想你们大多数人都知道该方程的含义——这是标准 ECDSA 签名的方程，其中 k?是加密安全的随机整数，m?（译注：原文此处写成了 n，应该是笔误）是消息哈希，x?是我们的 ECDSA 密钥，而 r?是曲线生成点的 k 次方（译注：原文此处多写了一个模?q，应该是笔误）。因此，这是一个标准 ECDSA 协议的方程。

所有这些方程都是在密文上完成的，因此最后我们的签名也被加密了：

我们需要处理它，这是在第 6 轮中完成的，在这一轮里所有参与者都执行门限解密机制以了解 s?的值。解密值 s?和在第4轮中评估的参数 r 共同构成签名：

我知道第一次见到它显然不容易理解。我的意图不是要让你对协议有一个全面的了解，而是要通过所有步骤了解你如何在后台进行工作。

因此，有两个注意事项。

实际上，这是关于被问到的问题的——签名协议的单点故障是不可接受的。在密钥生成这里是容易的，因为我们可以检测到一方是否有行为不当。我们有零知识证明和承诺。如果一方在密钥生成协议期间行为不当，我们可以删除结果，然后将行为不当的一方替换为其他人，然后重启协议。在签名这里就不那么容易了，因为即使一方行为不当，我们也应该能够产生签名。只要我们有 t?加 1，其中 t?是诚实的门限参与者——这是我们在生成加法同态门限加密方案时设置的参数——我们仍然可以生成一个签名。因此，我们需要一些最低限度的诚实参与者，然后就一切都好了。

另一个重要的注意事项是这些密钥是如何生成的。我们这里通常有两种可能的方法——有一个受信任的经办人设置，其中一方会生成那些密钥并将其交付给组中的所有其他参与者，而受信任的经办人应该忘记所有这些密钥，擦除内存。第二种可能性是我们执行某种无经办人协议，以便由所有组员一起执行密钥。还有明天史蒂夫可能还会提出第三种方法（http://stevengoldfeder.com/papers/GG18.pdf）。这两篇论文（编者注：https://link.springer.com/chapter/10.1007/978-3-642-17955-6_4和https://link.springer.com/article/10.1007/s10207-010-0119-9）显示了该设置的可能算法。

那么，它真的有效吗？是的，我们已经签名了许多以太坊和比特币交易。但重要的是要了解该解决方案确实是通用的，因此我们可以在此处使用任何椭圆曲线。

因此，不管你是一个钱包公司或提供机构托管解决方案，还是你只是想保护自己的个人钱包，你都可以受益于 t-ECDSA，尤其是在不支持多重签名的链上。因此，例如，作为一个加密货币交易所，你可以把以太坊密钥存储在多个服务器上，甚至可以将某些部分存储在线下，因此这应该降低了遭受攻击的可能性。

我们希望你享受这趟加密学之旅。

- The End?-

—-

编译者/作者：BixinInstitute

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。