原文标题:《零知识证明 - 椭圆曲线基础》 对椭圆曲线的学习,个人推荐如下的链接,没有太多的术语,解释的比较清楚。 https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/ https://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/ 本文也是在上述链接的基础上的总结。 1. 实数域上的椭圆曲线 1.1 定义 椭圆曲线的数学定义可以查看 Wolfram MathWorld:http://mathworld.wolfram.com/EllipticCurve.html。不是密码学或者数学专业的小伙伴,看的是一头雾水。便于工程理解,椭圆曲线是一系列满足如下方程的点:
并且 如下是 b=1, a 从 2 到-3 的椭圆曲线:
从方程可以看出,椭圆曲线是关于 x 坐标对称的曲线。除了坐标系上曲线的点,椭圆曲线额外定义一个点(无穷远处),记为 0。 也就是说,椭圆曲线是由如下的点组成:
1.2 基于椭圆曲线的群定义 在椭圆曲线的基础上,可以定义一个加法群: *所有椭圆曲线上的点,就是这个群里的元素 *单位元就是 0 *点 P 的逆元是点 P 相对 x 坐标的对称点 *加法定义如下:在椭圆曲线上,和一条直线相交的 3 个点 P,Q 以及 R,三点相加满足 结合群的定义,可以证明定义的这个加法群,就是阿贝尔群。 封闭性:因为椭圆曲线上的点相加,还是椭圆曲线上的点。 结合律: 单位元 : 单位元是 0 逆元 : 一个椭圆曲线上的点 P 的逆元,是相对 x 坐标的对称点 交换律: 1.3 椭圆曲线加法计算 因为
考虑几种特殊情况,对加法计算进行「修正」: * * *
*
1.4 加法计算推导 加法的定义是完备的。针对最普通的情况,就是在椭圆曲线上一条直线能穿过三个点,分别是 P,Q。
可以推导出:
或者
当然,如果 P/Q 是同一个点的话,斜率的计算公式不同。 1.5 标量乘法(Scalar Multiplication) 在加法的基础上,定义了标量乘法,同一个点相加多次:
计算标量乘法,最简单的方法是一个个 P 点相加。如果 n 是 k 位的话,算法复杂度是: 有个快速的计算方法:double 后相加。假设 n=151,二进制表示为: 还是用 n=151 举个例子:
"Double" 主要是依次获得某个位对应的变量的结果。如果该位是 1,就加到最后的结果中。这种算法的复杂度是: 1.6 对数问题 已知 n 和 P, 2. 有限域上的椭圆曲线 上面介绍的是基于实数的椭圆曲线的点,可以构造一个群。考虑特征数为的有限域,为素数。该有限域是由模 的结果组成,记 2.1 扩展欧几里得定理 给予二整数 a 与 b, 必存在有整数 x 与 y 使得 ax + by = gcd(a,b)。gcd(a,b) 是最大公约数。 2.2 模 p 运算下的乘法逆 假设元素 a,在模运算下,有逆元 x。满足,
通过扩展欧几里得定理,可以求得 x 和 y。x 就是 a 的乘法逆。 2.3 在 F_p 定义椭圆曲线 在
定义和实数上的定义类似。如下是
椭圆曲线是关于
在模 p 的情况下,这两个等式相等。 2.4 点加 和实数上椭圆曲线的点加类似,定义在一条「线」上的三点相加等于 0:
上图是 点加性质: * * * 2.5 点加计算 假设三个点在一条线上,
从而,推导出:
其他条件下的推导,涉及的公式比较多。有兴趣的小伙伴可以自行推导。 2.6 在有限群上的椭圆曲线有多少点? 椭圆曲线上的点的个数,称为「阶」。如果枚举 0~p-1,查看点的个数,不太现实,因为 p 是一个非常大的质数。Schoof 算法能在多项式时间确定椭圆曲线阶:https://en.wikipedia.org/wiki/Schoof%27 s_algorithm。 2.7 标量乘法 和实数域上一样,可以使用 double 后相加的方法计算。在有限域上,有额外的特性,举个例子:
已知
…
很容易看出,在有限域上的椭圆曲线中一个点标量乘法的结果,组成一个在加法操作下的循环子群。在子群中的点,所有的加法的结果都还在子群中。而且,存在一个点,幂次(加法操作)能生成子群中的所有点。这样的点,称为「生成元」。 绕了一大圈,在有限域上的椭圆曲线上,存在很多个循环子群。子群是基于加法操作。 2.8 循环子群的阶 Schoof 算法能确定整个基于有限域上的椭圆曲线上的点的个数,但是不能确定循环子群的个数。
https://en.wikipedia.org/wiki/Lagrange%27 s_theorem_(group_theory) 该定理给寻找循环子群的阶 n,提供了一个思路: 1/ 利用 Schoof 算法,计算出整个椭圆曲线的阶 2/ 找出其所有的约数 3/ 找出最小的约数 n,满足 2.9 寻找生成元 通常使用椭圆曲线算法,先选择曲线,计算椭圆曲线的阶,然后在这条曲线上找到最大的子群。找子群,就是寻找子群对应的生成元。 假设椭圆曲线的阶为 N,子群的阶为 n,由拉格朗日定理, 又因为椭圆曲线的阶为 N,P 为椭圆曲线上的随机的点,存在 则 2.10 离散对数问题 已知两个在子群上的点 P 和 Q,求解 2.11 同态 如果子群的阶为 r,则 *同态加法 : 总结: 有限域上的椭圆曲线是零知识证明的基础。零知识的实现是基于离散对数问题。从计算的角度来看,F_p 是个有限域,在之基础上建立的椭圆曲线点的运算都是在这个域范围内。有限域上的椭圆曲线上有很多循环子群 F_r,具有加法同态的特性。离散对数问题指的是,在循环子群上已知两点,却很难知道两点的标量。 来源链接:weixin.qq.com 区块律动 BlockBeats 提醒,根据银保监会等五部门于 2018 年 8 月发布《关于防范以「虚拟货币」「区块链」名义进行非法集资的风险提示》的文件,请广大公众理性看待区块链,不要盲目相信天花乱坠的承诺,树立正确的货币观念和投资理念,切实提高风险意识;对发现的违法犯罪线索,可积极向有关部门举报反映。 —- 编译者/作者:区块律动BlockBeat 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
零知识证明:椭圆曲线基础
2020-01-19 区块律动BlockBeat 来源:区块链网络
- 上一篇:数字货币的核心和本质
- 下一篇:我们如何看待区块链的匿名性,它真的匿名吗?
相关阅读:
- 微软推出首个无需做可信设置的 zkSNARK 技术方案 Spartan2020-08-03
- 为何我理解不了零知识证明:ZKP常见误区分析2020-07-17
- 研究员表示:比特币的椭圆曲线可能有一个秘密的后门2020-07-02
- 加拿大银行研究人员:零知识证明还不够成熟,无法用于CBDC2020-07-01
- Gate.io研究院:零知识证明于区块链中的落地应用2020-06-28






 。该方程称为椭圆曲线的 Weierstrass 方程。
。该方程称为椭圆曲线的 Weierstrass 方程。

 。也就说,椭圆曲线上的两点相加的结果,还在椭圆曲线上。
。也就说,椭圆曲线上的两点相加的结果,还在椭圆曲线上。

 。计算
。计算 的方法就比较直观了:连接 P 和 Q 划一条线,该线和椭圆曲线交的另外一个点为 R。
的方法就比较直观了:连接 P 和 Q 划一条线,该线和椭圆曲线交的另外一个点为 R。
 或者
或者 :因为定义 0 为无穷远处,不能基于无穷远处划线。但是因为定义了 0 为单位元,所以
:因为定义 0 为无穷远处,不能基于无穷远处划线。但是因为定义了 0 为单位元,所以 以及
以及 。
。 :因为两个点是对称的,所以基于这两个点划的线垂直于 x 轴,不再相交于其他点。
:因为两个点是对称的,所以基于这两个点划的线垂直于 x 轴,不再相交于其他点。 。
。 :如果 P 和 Q 是同一个点的话,那存在多条线穿过这「两个」点。如果把 Q 看作是无限接近 P 的过程,可以看出,穿过 P 和 Q 的是椭圆曲线在 P 点的切线。如果切线和椭圆曲线相交的点为 R,则
:如果 P 和 Q 是同一个点的话,那存在多条线穿过这「两个」点。如果把 Q 看作是无限接近 P 的过程,可以看出,穿过 P 和 Q 的是椭圆曲线在 P 点的切线。如果切线和椭圆曲线相交的点为 R,则 ,
, 。
。
 ,并且不存在第三个点相交:这种情况和上一种情况有点类似,也就是说,P/Q 的连线是椭圆曲线的切线。如果 P 点是切点,
,并且不存在第三个点相交:这种情况和上一种情况有点类似,也就是说,P/Q 的连线是椭圆曲线的切线。如果 P 点是切点, 。也就是说,
。也就是说, 。
。
 。这条直线有个斜率:
。这条直线有个斜率:



 。
。 。
。
 。
。 的计算比较容易。但是,在 Q 和 P 已知的情况下,求解 n 非常困难,没有多项式时间求解算法。
的计算比较容易。但是,在 Q 和 P 已知的情况下,求解 n 非常困难,没有多项式时间求解算法。 。因为有限域中的元素都有逆元,也就是
。因为有限域中的元素都有逆元,也就是 ,则
,则 。
。 。也就是说,
。也就是说, 。
。
 ,p 分别是 19,97,127,487 对应的椭圆曲线的点。
,p 分别是 19,97,127,487 对应的椭圆曲线的点。
 对称,因为
对称,因为

 。
。
 的椭圆曲线,其中
的椭圆曲线,其中 。图中的黄色的一系列的斜线是
。图中的黄色的一系列的斜线是 的直线。R 就在其中一条斜线上,-R 就是图中标出的 R 的对称点,也就是 P+Q 的结果。
的直线。R 就在其中一条斜线上,-R 就是图中标出的 R 的对称点,也就是 P+Q 的结果。
 ,也就是,-Q 是横坐标相同但纵坐标相反的点,也就是,相对 p/2 对称的点。
,也就是,-Q 是横坐标相同但纵坐标相反的点,也就是,相对 p/2 对称的点。
 ,
, ,
, 。如果 P 和 Q 不是同一个点:
。如果 P 和 Q 不是同一个点:


 以及点
以及点 。点 P 的标量乘法的结果是循环的,只有五个点。
。点 P 的标量乘法的结果是循环的,只有五个点。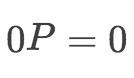











 。
。 。也就是说
。也就是说 。
。 为子群的生成元。
为子群的生成元。 是非常难的问题。目前该问题没有多项式时间求解算法。
是非常难的问题。目前该问题没有多项式时间求解算法。 。
。

