零基础理解隐私保护技术「防弹证明」与「Supersonic」

理解两类零知识证明技术「防弹证明」与「Supersonic」，你需要先了解机密交易与密码学承诺等概念。

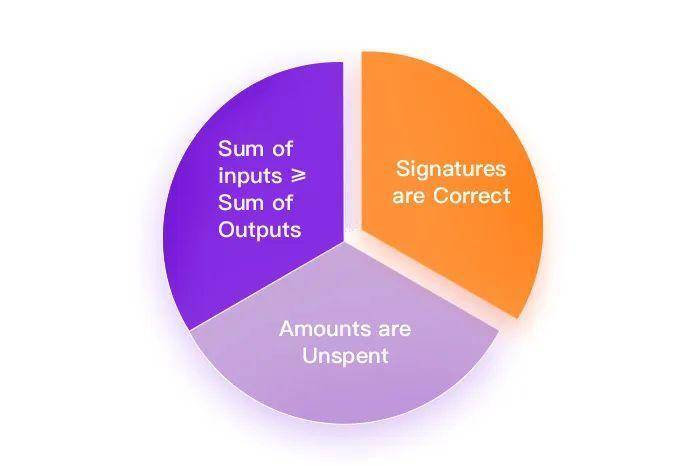
原文标题：《了解 zk-SNARK 技术——零基础详解防弹证明与 supersonic》
撰文：Cent

当前区块链所涉及的问题当中，隐私被普遍是认为是重中之重，比特币、以太坊以及 Libra 的隐私性都很糟糕，而对此相关的技术解决方案也在不断涌现而出，想要同时兼顾隐私和可审计性，可使用零知识证明方案来解决，从最初门罗币使用的环签名到 Zcash 使用的 zk-SNARKs，再到 Bulletproofs （防弹证明）以及 Supersonic （超音速证明）的出现。隐私解决方案的发展，日新月异。

在开始本篇的介绍之前，先让我们回顾一下上一篇文章中关于 zk-SNARK 的相关知识。

我们了解了 zk-SNARK 实际上是一种带有零知识特性的非交互简洁论证，而这个技术的最大问题是证明者和验证者之间需要一个「初始化可信设置」，由此可能带来信任问题。对于 zk-SNARK，「初始化可信设置」是新技术努力尝试克服的最核心问题。

在这篇文章中，我们将主要讲述两种已知的可以比较好的解决这个问题的零知识证明技术。

防弹证明与 Supersonic 是加密技术新的突破，但也可以说成是当时先进的一些加密技术思想的非常巧妙的结合。具体地说，它们起源于一些隐私协议的思想，例如机密交易和零知识证明和密码学承诺。我们已经了解过什么是零知识证明，因此，在了解防弹证明和 Supersonic 之前我们先要了解一些机密交易、密码学承诺相关的概念。

机密交易「一个黑盒子」

笼统地讲，您可以将机密交易视为一笔类似于比特币交易的技术，但是不同的是其中金额是机密的。这意味着只有发送者和接收者才能知道实际金额。但是很酷的一点是，即使完全不知道交易的金额，也可以通过第三方验证交易是否正确。这些验证者可以看到谁发送给谁，他们可以看到交易中有多少输入和输出，但是他们看不到涉及的金额。

在 2016 年，格雷格·麦克斯韦（Greg Maxwell）引入了机密交易的概念，该概念用可以由接收方验证的加密承诺有效地取代了交易金额。加密方式通常基于 Pedersen 承诺，这是一种可以表达有关值的语句的方法，该语句可以在隐藏值本身的同时进行验证。机密交易当然可以使用可验证的签名和未花费的金额来实现安全交易，但无法使接收者验证输入的金额大于输出的金额。这就是零知识证明发挥作用的地方。

零知识证明通过允许接收者向发送者挑战以证明特定的内容来扩展机密交易。从隐私的角度来看，该技术非常有效，但它们却大大增加了交易的规模，并且经常需要可信任的设置。而这也是我们需要解决的问题。

机密交易的实现过程

如果我们考虑验证加密货币交易所需的步骤，可以将它们概括为三个步骤：签名正确：交易来自有效节点，未用金额：没有重复支出问题（双花），输入的总和大于输出的总和：具体来说输出 = 输入-交易费用。

那么这个过程是如何实现的呢？我们考虑一个加密货币情境下的交易问题：

小明希望在小红那里购买一部手机，小红从小明那里获得了 1BTC，而小明想以 0.1BTC 的价格购买手机。在这种情况下，小明将创建一个输入为 1BTC 的交易，支付输出为 0.1BTC，并且找回的零钱输出为 0.9BTC。

当比特币网络的某个节点验证交易时，它会确保交易成功 1 = 0.1 + 0.9。请注意，现实世界存在交易费用，这个式子没有包含交易费用。缺少了一部分，在这个例子中我们可以忽略掉它，以简易化这个知识点的概念。

机密交易的想法基于这样的认识，为了良好的隐私性，验证节点不必知道具体金额，只需要知道：

sum of inputs = sum of outputs

（总输入 = 总输出）

而事实上确实有一种类似魔法的加密技术可以隐藏类似金额信息而验证这样的等式：

在密码学中这被称作密码学承诺。

但是这又引进了一个新的问题，对于：

C(1) = C(100) + C(-99)

上面的验证也可以通过，但这实际上凭空创造了 100BTC。因此，我们还需要限制每个承诺的界限，或者说范围。

防弹证明

「范围证明使任何人都可以验证承诺代表指定范围内的金额，而无需透露其价值的任何其他信息。」

防弹证明是范围证明（range proofs）的一种更有效的形式，是非交互式零知识证明协议的新实现，不需要信任的设置。防弹证明基于现有的范围证明方法，可将多个范围证明合为一个，且其数据比以往方法还要小。有趣的是，防弹允许聚合验证，这意味着您可以通过将多个验证聚合起来，一起进行，这相比较一个一个验证的话，效率有很大的提高。

防弹证明的证明数据量比较短，而且有很好的隐私保护，但是对比于其他新的零知识证明技术较慢，因此它可能不适用于特别复杂的证明，比如说交易的时候要隐藏金额，我们就可以用防弹证明。但是对于类似偿付能力证明这样内容较为复杂的证明，防弹证明就不再适合。而在应用上，Monero 中对防弹证明进行的早期测试中，交易规模和费用减少了 80％，这是一个巨大的进步。

Supersonic

2019 年 10 月 22 日，Findora 联合创始人，斯坦福密码学家 Ben Fisch 和 Benedikt Bünz，以及 Alan Szepeniec 发布了他们在零知识证明方面的最新突破，即「Supersonic」（超音速）。（Benedikt Bünz 也是防弹证明的发明者之一）

Supersonic 证明是第一个实用，不可信，简洁且可有效验证的零知识证明，Supersonic 的验证证明数据小于 10 KB，并且仅需要 7 毫秒便可验证一个 10 万个逻辑门的语句。Supersonic 和防弹证明适用于不同的语句。一个机密交易的语句大概需要 4000 个逻辑门，相比较来讲，一个完全匿名的交易语句则需要 10 万个逻辑门。一般情况下，适用防弹证明的机密交易所提供的交易隐私已足够满足日常生活所需要的隐私，并且可以与别的区块链隐私工具合并使用增加隐私性，例如把多个交易合并在一起的 CoinJoin 工具。但是在用户必须要完全保密所有信息的情况下，交易可以使用 Supersonic 来构造应对与更复杂的语句的零知识证明，并且不会在速度和时间上造成损失。

Supersonic 技术原理浅析

在上篇我们讲述 SNARK 的相关知识时，我们提到了 SNARK 在验证知识时，会将一段陈述转换为多项式证明的形式。而在实际应用中 PCP （概率可检验的证明）和更一般的多项式 IOP 具有很好的特性，即仅对某些多项式进行几次评估就足以确定要证明的陈述的真实性。

但是，我们之前提到，这里有一个小问题：证明者必须将整个多项式发送给验证者（将导致冗长的证明，这对于 SNARK 来说是不利的属性），或者证明者必须以某种方式执行验证者评估。利用密码学承诺技术，SNARK 使用加密方法仅发送多项式的简短承诺，而不发送整个多项式，这大大减少了证明方和验证方之间的通信。

Sonic，PLONK，Fractal 和 Libra 均使用应用于多项式 IOP 的多项式承诺方案。有趣的是，多项式的选择和使用的承诺方案在很大程度上彼此独立。因此，通常可以将一个 SNARK 的多项式 IOP 与其他 SNARK 的多项式承诺方案一起使用。这意味着多项式 IOP 的开发和多项式承诺方案的开发可以分别进行，这就是 Supersonic 的情况。

Supersonic SNARK 为现有的多项式 IOP （例如 Sonic，PLONK 或 Marlin）引入了一种新的，有效的多项式承诺方案，可以移除 SNARK 中的初始化可信设置。Supersonic 中使用的多项式承诺方案（以前未用于 SNARK）称为 DARK （Diophantine Arguments of Knowledge）。而由于多项式承诺比多项式小得多，我们明显缩小了多项式 IOP 的「证明」大小，同时引入了一个新的假设，即证明方在证明上滥用承诺方案在计算上是不可行，这将产生错误陈述的「证明」。

这使得对于复杂的陈述，Supersonic 的综合证明大小和验证时间在最新技术上得到了超过一个数量级的改进。在这类应用中，它们至少比 STARK小 50 倍，并且比 Bulletproofs 的验证速度快 1000 倍。」

Findora 的联合创始人兼研究主管 Benedikt Bünz 表示：「这一突破的意义在于其将零知识证明的实用性和能力提升到一个新水平的能力。许多零知识解决方案的关键问题是证明量大，消耗存储和带宽，并且验证交易证明可能是一个非常漫长的过程。先前的解决方案要么不切实际，庞大，缓慢，要么并非真正不可信。通过消除对可信设置的需求，Supersonic 将使 Findora 能够解决区块链的一些最大风险和问题，例如隐私，合规性和选择性披露问题。

在这篇文章中，我们介绍了两种最近零知识证明相关技术的发展，这些技术在 Findora 的区块链技术平台中都发挥了巨大作用，而之后我们也会持续地更新介绍关于密码学和零知识证明的科普知识。

本文来源：Findora
原文标题：零基础理解隐私保护技术「防弹证明」与「Supersonic」

—-

编译者/作者：Findora

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。