梦想中的一个完美的swap交易所

一.基于AMM的swap交易所具有哪些痛点

1.一类无常损失

2.二类无常损失

3.有限深度

4.滑点大

5.流动性资金浪费

6.如何快速积累VC

如果有一个swap能一次性解决以上五个问题，

1.消除一类无常损失

2.消除二类无常损失

3.无限深度

4.消灭滑点

5.高vault收益

6.抢夺VC

我愿称你为完美的swap交易所。比如下面的unisave的设计

1.1 什么是一类无常损失

当我们为一个交易对，提供交易对（pair）的流动性时（liquidity）。引用DODO白皮书中的说法。我们实际提供的是一份quote token以及一份base token(常见为稳定币或者ETH)

在没有任何人进行交易的前提下。我们依旧可能因为quote token自身的外部币价单边行情下跌。蒙受无常损失。

我称之为一类无常损失。

1.2 如何消灭一类无常损失——Balancer的98：2范式

不同于Uniswap写死的quote token和base token的 50：50比例。在balancer的可调比例之下，产生了98：2的新范式。

在这个新的范式中，如果我们把base token比例设置为98，quote token比例设置为2.

quote token的涨跌将几乎不再影响我们的LP资产价值

特别的有 当quote token 价格下降80%，LP价值一类无常损失仅为3.2%。当当quote token 价格下降99%，LP价值一类无常损失仅为8.8%

1.2.1例子：

对于98：2的Balancer， MKR-ETH池的流动性凭证BPT来说

如果MKR对法币的代币价格翻番，ETH价格对法币不变，BPT价值将增加97%（=2^0.98=1.97）

而对于50：50比例的MKR-ETH Uniswap池中LP token来说

如果MKR对法币的代币价格翻番，ETH价格对法币不变,Uniswap LP的价值将增加41.4%（=2^0.5=1.414）。

不难发现，如果我们关闭swap类交易所的交易功能，LP token的价值近似一个关于base token的指数基金。只要base token(常见稳定币、eth)不发生暴涨暴跌，该98：2范式可以消除1类无常损失

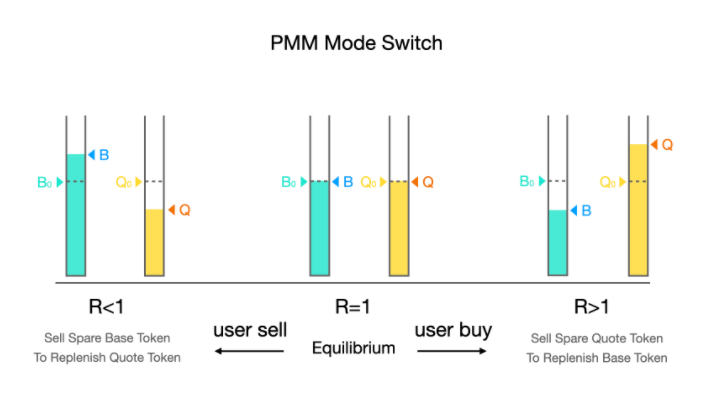
1.2.2具体实现方法，参考balancer的白皮书

https://balancer.finance/whitepaper/

2.1什么是二类无常损失

即便quote token 与base token的法币价值并不发生半边行情，而只是上下波动时。我们知道，因为AMM类swap交易所并无法感知外部价格的变动,始终会使用swap内部价格与trader进行交易。这样在套利者不断搬砖套利抹平价差的同时，我们必须思考，这些套利者也在源源不断地套走AMM做市商的LP资产价值。这种在震荡行情中产生的无常损失，我称之为二类无常损失

2.1.1二类无常损失计算器

https://baller.netlify.app/

2.1.2二类无常损失计算公式

deltaP = (1 + priceChange1) / (1 + priceChange2)

iL = 1 - (deltaP ^ weight1) / (weight1 * deltaP + weight2)

2.2如何消灭二类无常损失——dodoswap 的PMM算法

2.2.1 PMM做市算法的三种状态

在Dodoswap的假设中。他认为在传统的AMM做市算法中，存在着三种状态。

1.uniswap价格和外部价格保持一致，该种状态下，不存在套利空间，传统uniswap算法完美

2.uniswap价格较于外部价格被高估，此时套利者可以通过外部买入，uniswap卖出的形式。抹平价差同时，套走AMM的LP价值

在该种情况下dodoswap的方案是，通过预言机，读取外部资产价格。不再使用传统的uniswap AMM 算法执行交易。而是使用 PMM算法，使实际成交价格更接近外部价格。以此极大抹除第二类无常损失。并且降低滑点。

3.uniswap价格较于外部价格被低估，此时套利者可以通过uniswap买入，外部卖出的形式。抹平价差同时，套走AMM的LP价值

在该种情况下dodoswap的方案是，通过预言机，读取外部资产价格。不再使用传统的uniswap AMM 算法执行交易。而是使用 PMM算法，使实际成交价格更接近外部价格。以此极大抹除第二类无常损失。并且降低滑点。

2.2.2 PMM算法的数学表达

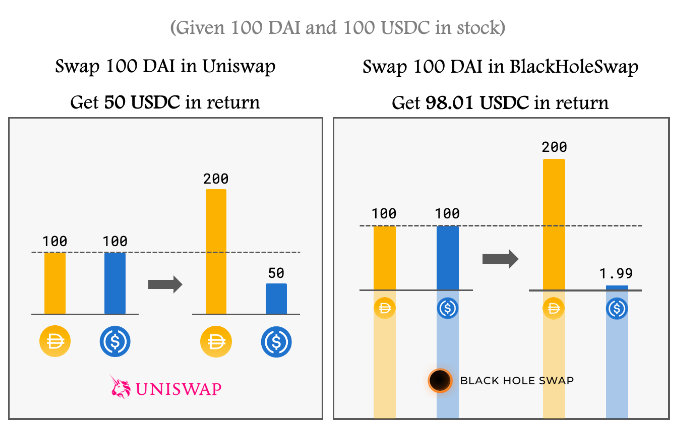
2.2.3 更多关于PMM的数学原理与代码呈现

https://dodoex.github.io/docs/docs/

3.1滑点大小与交易深度的悖论

在传统的uniswap AMM交易算法中，保障无限交易深度的基础是滑点。滑点越大，交易深度越好。滑点越小，交易深度的消耗越快。这一点不难理解。那么是不是意味着，任何改善滑点问题的算法无论是curve,bancor v2,dodo的PMM，hakka的blackswap，都意味着对交易深度的牺牲呢？

并不是的，我们在hakka的白皮书中找到了解决方案。

3.2.1hakka中使用的blackhole 算法

如下图

由于在hakka的blackhole swap当中，几乎没有滑点。如右图，经常会发生。交易深度枯竭的现象。此时我们知道当蓝色代币深度不足时，黄色代币一定是荣誉的。因此hakka结合了lend、compound等借贷平台。在蓝色货币不足时，抵押黄色货币来借贷蓝色货币。来补足蓝色火币的流动性，进而使该算法下滑点几乎没有的同时，交易深度接近无限。类似的设计我们也可以在curve的设计中找到。

3.2.2blackhole swap 算法白皮书：

https%3A%2F%2Fblackholeswap.com%2Fdocuments%2Fen.pdf

4.如何消除滑点

其实我们在2.2节中已经找到一种利用预言机来极大削弱滑点的算法PMM算法，我们又在3.2.1中了解到了近乎消灭滑点的blackhole算法。那么该算法是如何实现的呢？

数学原理上，实际是对AMM进行了线性变换

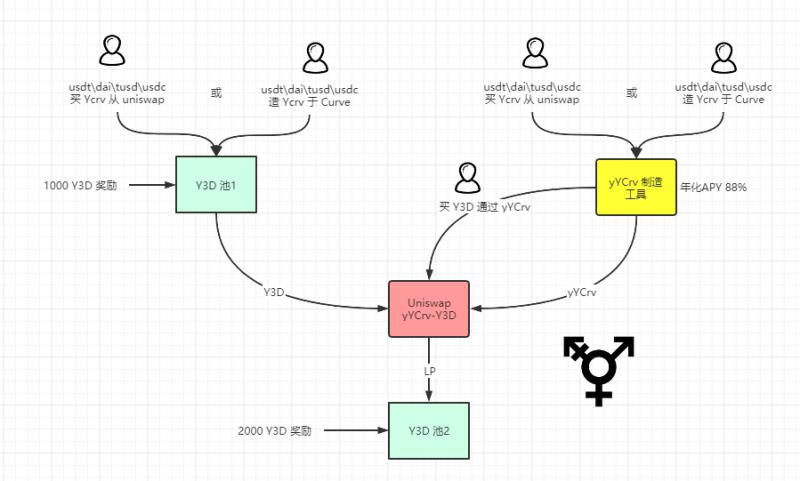
5.如何盘活流动性池子中的质押资金

第一我们了解到在blackhole swap算法中。会利用一部分冗余资金进行抵押借贷，闲置时赚取抵押收益的同时，为swap提供了近乎无限的交易深度

我们又知道在dodoswap中，有一种流动性倾向的概念，算法会尽量把流动性移动到即将发生交易的价格区间处，让滑点更小

但是Y3D团队提出的Liquidivault概念先然更好。在该算法下。所有闲置在流动性池子的货币。全部以Vault的形式被利用。根据策略合约进行借贷、挖矿等投资行为。再以流动性挖矿的形式把利润返还到用户手中可谓最为合理

6.sushiswap的强盗逻辑

Sushiswap为我们提供了一个非常有创业的掠夺VC形式。相信已经很多文章介绍过了，这里不做赘言

7.Y3D项目第一阶段完成了哪些壮举

1.(usdt\usdc\tusd\dai)->ycrv+crv=yycrv

stake ycrv

unstake yycrv

2.usdt<->yycrv

deposite

mint

claim

restore

3.ycrv->y3d & y3d-yycrv pair

stake

unstake

claim

exit

&

stake y3d0yycrv LP

unstake y3d-yycrv LP

—-

编译者/作者：animaeos

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。