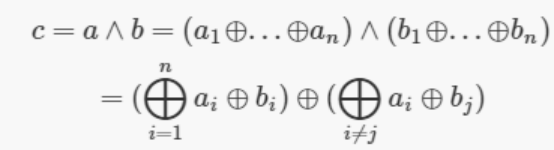| 混淆电路(Garbled Circuit),又称姚氏电路(Yao’s GC)是由姚期智教授于1986年针对百万富翁问题提出的解决方案。 导读:混淆电路(Garbled Circuit),又称姚氏电路(Yao’s GC)是由姚期智教授于1986年针对百万富翁问题提出的解决方案。 它的核心技术是将两方参与的安全计算函数编译成布尔电路的形式,并将真值表加密打乱,从而实现电路的正常输出而又不泄露参与计算的双方私有信息。由于任何安全计算函数都可转换成对应布尔电路的形式,相较其他的安全计算方法,具有较高的通用性,因此引起了业界较高的关注度。 混淆电路发展 姚氏电路是基于半诚实模型(semi-honest)的安全两方计算(Two-Party-Security-Computation)。 简单来说,可将整个计算过程分为两个阶段: 第一阶段将安全计算函数转换为电路,称之为电路产生阶段; 第二阶段,利用OT、加密等密码学原语等执行电路,称之为执行阶段。 每一阶段由参与运算的一方来负责,直至电路执行完毕输出运算后的结果。针对参与运算的双方,从参与者的视角,又可以将参与安全运算的双方分为电路的产生者(circuit generator)与电路的执行者(circuit evaluator)。 示意图如下所示:
▲步骤一:电路产生阶段 参与运算的双方先就需要安全计算的目的依靠专有编程语言(DSL)或相关编程语言扩展等进行编程,然后针对实现计算的程序进行编译,生成布尔电路文件; 然后针对双方输入值以及中间输出结果随机产生映射label,再利用这些label做为key对每个对应的电路输出真值表采用分组密码方式进行加密,并对真值表值进行打乱操作,这一步就是混淆电路的概念。 ▲步骤二:电路执行阶段 电路执行者针对布尔电路文件进行执行,执行时电路生成者需要将自己的输入所对应的label发给电路执行者;电路执行者依据自己所有信息通过OT方式选择自己对应的label,这样电路生成者与执行者均不到对方的输入数据;电路执行者此时获取双方输入对应的label,作为key的相关信息对真值表进行解密,即可获取真值表的内容,循环往复,直至所有电路执行完毕,输出执行结果。 姚氏电路是第一个安全两方计算协议,后续大多数安全地计算布尔电路/算术电路的安全多方计算协议都是基于姚氏混淆电路进行扩展的。 比较常见有GMW/CCD/BGW/BMR等,这些协议将姚氏协议支持的两方安全计算扩展到多方安全计算;将布尔电路扩展到算术电路;将安全模型由半诚实模型扩展到恶意模型,以抵抗一定数量恶意敌手攻击。 上期文章已经就两方安全计算混淆电路进行介绍,我们在此基础上介绍下支持多方安全计算协议GMW。 GMW协议介绍 GMW协议是由Goldreich等人提出,支持多方(2+)安全计算,它不但支持布尔电路还支持算术电路。但与姚氏电路协议略有不同,电路评估时不再使用混淆的真值表,而是在本地直接进行计算,这样大大节省混淆真值表带来的解密操作,节省比较多的计算量。 GMW协议采用秘密分享及OT等常见的加密原语,可将整个计算过程分为三个阶段: ▲秘密分享阶段 参与运算的多方将自己的私有数据采用线性秘密分享方式对参与运算的多方进行秘密分享,保证每一个参与方都可以获得自己秘密的分量。 ▲电路执行阶段 将接收到的每个秘密分量输入到电路中,本地逐门执行电路(AND门需要再执行OT协议),重复此过程,直到所有门都执行完成,获得结果的分量。 ▲结果广播再计算 每一方将最后的执行结果广播出来,各参与方获得各个参与方结果分量后求取最终结果。 举例分析 参与运算的双方有Alice和Bob: Alice拥有私密信息u,将秘密进行加法秘密分享(additive secret sharing)后,使得[u1]⊕[u2]=u,[u1][u2]可以看作u的秘密分量,Alice将[u2]发给Bob; Bob拥有私密信息v,将秘密进行分拆后,使得[v1]⊕[v2]=v,[v1][v2]可以看作v的秘密分量,Bob将秘密分量[v1]发给Alice。 这样Alice与Bob都拥有彼此的秘密分量,如下表所示:
Alice与Bob安全计算和(异或门),表示成电路形式如下所示
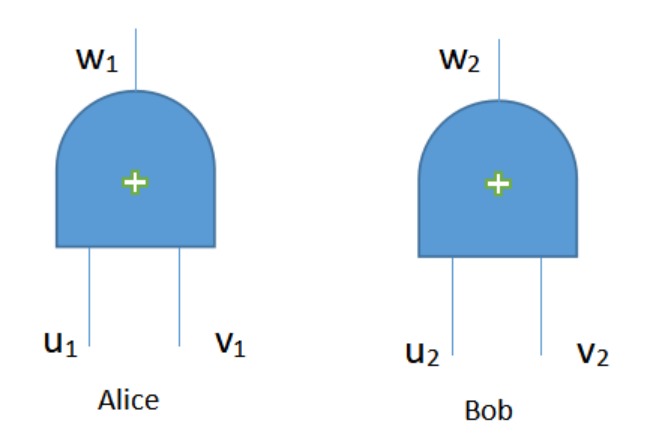
Alice和Bob进行秘密分享后,Alice与Bob获取的秘密分量及计算电路如下所示:
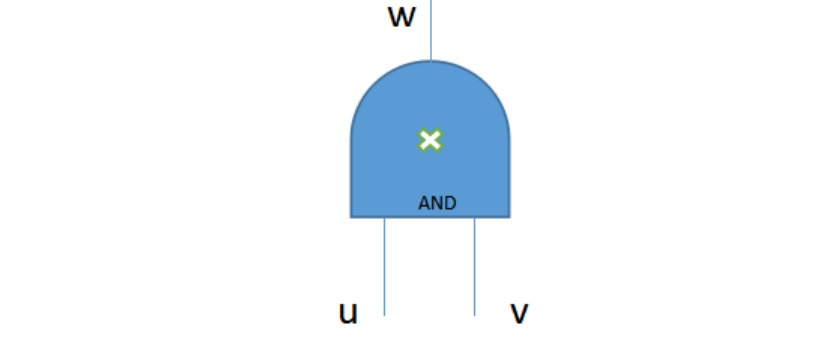
Alice与Bob分别在本地执行此电路: Alice:u1⊕v1= w1Bob:u2⊕v2= w2 Alice与Bob分别将执行电路后的结果分量广播出去,本地计算后获取最终结果: w1⊕w2= (u1⊕v1)⊕(u2⊕v2) = (u1⊕u2)⊕(v1⊕v2)(异或满足交换律) =u⊕v (2)布尔电路之AND(相当于乘法) Alice与Bob安全计算乘积(and门),其表示成电路的形式如下所示:
Alice和Bob进行秘密分享后,Alice与Bob获取的秘密分量及计算电路如下所示:
Alice本地计算AND门时,求得u1v1 Bob本地计算AND门时,求得u2v2 可以发现还缺少其他分量u1v2⊕v1u2,此时GMW协议构造1-4 OT进行计算,Alice作为sender,拥有变量u1,v1,Bob拥有选择bit变量u2和v2,作为receiver。 记T=(u1v2)⊕(v1u2),Alice在构造1-4 OT时,对真值表加了干扰σ⊕T,这样做的目的主要是防止Bob根据T的结果推测出Alice的秘密分量u1。
经过1-4 OT后,双方值情况如下: Alice计算得到的值为:u1v1⊕σ Bob计算得到的值为:u2v2⊕σ⊕T Alice与Bob分别将本方的结果分量广播出去,本地计算后获取最终结果: w = u1v1⊕σ⊕u2v2⊕σ⊕T = u1v1⊕u2v2⊕T = u1v1⊕u2v2⊕(u1v2⊕v1u2) = (u1+u2)⊕(v1+v2) 三方或者更多方扩展 (1)异或门(XOR) 各参与方获得各个分量后本地执行电路,与两方计算类似,然后广播自己本地计算结果,当收集全各个参与方自己计算结果时再计算最终结果。 (2)与门(AND) c=a∧b,a1...an,b1..bn代表a,b分量
每个参与方本地计算ai⊕bi,然后每两个参与方相互组合计算ai⊕bj 最后各参与方广播自己最终本地计算结果(a∧b分量),求得最终安全计算结果a∧b 总结 混淆电路的优化可以分为两个方面: 一方面:电路优化(circuit optimization),主要是减少编译后电路的size,常用技术有free-xor/Garbled row reduction/Circuit simplification等; 另一方面:执行阶段优化,常用的技术有fast table lookup(减少解密混淆真值表次数)和pipelined circuit execution(将原来电路的产生与执行两阶段转换成一个阶段,一边产生一边执行电路,这样可以提高安全计算的效率)。 基于姚氏混淆电路进行扩展的协议与方法,大多已不再使用混淆真值表的做法,只保留电路的形式,且为了扩展至多方(2+)安全计算,普遍采用秘密分享/不经意传输等技术。 相较其他安全计算方案,混淆电路是一种比较通用的解决方案,安全性相对高,但其性能一般,尤其是当参与运算多方数目超过3+且数据量较大时,安全计算的过程中通信量会比较大(两方各1000个数据情况下求PSI通信量可达到GB数量级),特别不适合带宽受限或WAN网络环境下使用。 所以业内给混淆电路的评价是“efficient but expensive”,有效但计算代价比较高。 作者简介滕海明 来自趣链科技数据网格实验室BitXMesh算法研究团队 研究方向:数据安全 本文来源:趣链科技桔子 —- 编译者/作者:趣链科技桔子 玩币族申明:玩币族作为开放的资讯翻译/分享平台,所提供的所有资讯仅代表作者个人观点,与玩币族平台立场无关,且不构成任何投资理财建议。文章版权归原作者所有。 |
安全多方计算之混淆电路
2020-10-10 趣链科技桔子 来源:火星财经
相关阅读:
- 币小秘:明明看对了行情,为何就是做不对?2020-10-10
- 【善水论币】——大饼最新策略2020-10-10
- 买不起房,就多买两套,背后是怎样的投资智慧2020-10-10
- 以太坊2.0将开启质押模式 你有足够多的筹码吗2020-10-10
- 疫情网络微投电投靠谱的平台可以随时看现场情况2020-10-10





 (1)布尔电路之XOR(相当于加法)
(1)布尔电路之XOR(相当于加法)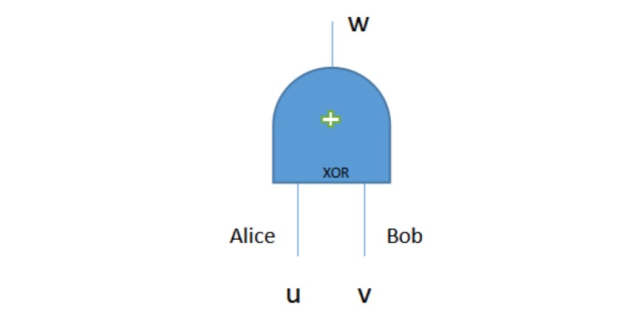

 σ⊕α3
σ⊕α3