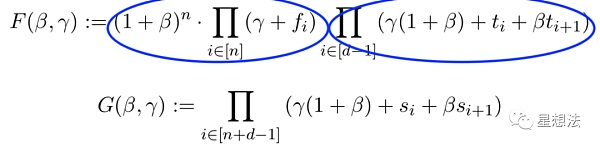零知识证明：Plookup算法介绍

最近有空看了看Plookup的论文。针对对电路描述不友好的操作（比如bit操作），Plookup给出了新的思路和证明方式。给定某个操作的真值表示（lookup table），证明某个操作的输入/输出是在真值表中。这种方式，相对之前的bit计算约束方式，降低约束的个数，提高了电路效率。

Plookup的论文下载地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup尝试解决的问题是，给定两个集合，证明某个集合的元素在另外一个集合中。给定两个集合t和f，s是f排序后的结果。如果t中的元素最少在f中出现过一次。判别f中的元素是否包括在t中，只需要比较元素差的集合：

举个例子，t是{1，4，8}的集合，元素的差异集合为{3, 4}，分别是4-1，8-4。如果s只有t中的元素组成，并且每个元素最少出现一次，例如{1，1，4，8，8，8}，元素的差异集合也为{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差异集合一样的情况下，也不能说明s中元素在t的集合中。例如s为{1，5，5，5，8，8}，元素的差异集合也为{3，4}，分别是8-5，5-1。

论文提出，可以引入一个随机因子，将前后两个元素相加的方法，确定两个集合的依赖关系。

定义多项式

在基本思想的基础上，论文在第三章定义了两个多项式F和G：

如果F和G相互对等，有且如下的条件成立：

f集合属于t

s是(f，t)的并集，并且按照t中的元素排序

如果条件成立，可以推导出两个多项式相等。F多项式可以看成是两部分组成，分别是两个连乘。后面的连乘可以看成是t中的元素连乘。前面的连乘，可以看成是f中元素的连乘。因为f中的元素属于t，则f中的元素的连乘，可以想象成多个相同元素的连乘。反之，因为beta和gamma的随机因子，也能从F和G对等条件推出满足的两个条件。具体的证明过程，可以查看论文的第三章。

在定义多项式的基础上，问题可以转化成两个多项式相等。

Plookup协议

已知f和t，可以排序得到s。因为s由f和t合并而成，s可以由两个函数h1和h2表示。关键在于第4步，定义了Z函数：

Z(g) = 1 - 初始为1

Z(x) 是两种多项式表示的商

Z(g^(n+1)) = 1 - n+1元素的连乘，两种多项式表达式相等

验证者，除了查看Z函数外，额外还要查看h1/h2连续性。

论文进一步将协议推广到更通用的情况，并给出了t中元素是连续情况下的优化协议。感兴趣的小伙伴可以自行查看。

总结

Plookup提出了一种明确输入/输出的情况下，如何证明某个函数的运算正确的协议。输入输出定义成lookup表，计算的输入/结果只要在该lookup表中即表示运算正确。和Plonk采用同样的思路，Plookup定义了问题的多项式表示，证明了Z函数的递归表示和边界。

—-

编译者/作者：星想法

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。