玩币族移动版

原文作者：0xTodd，Ebunker 联创

编者语：今年 5 月，Vitalik Buterin 重新发布了他在 2020 年发布的全同态加密（FHE）文章。该文章深入地介绍了 FHE 的相关数学工作原理。昨日，Ebunker 联创 0xTodd 在 X 上用通俗易懂的语言解释了 FHE 全同态加密的内涵与应用场景，BlockBeats 转载全文如下：

最近行情不佳，终于时间充裕了一些，可以继续分享一些新的技术路线。尽管 2024 年的加密市场不如过去那样波澜壮阔，但依然有一些新的技术试着走向成熟，比如说我们今天要聊的主题：「FHE / 全同态加密（Fully Homomorphic Encryption）」。

V 神在今年 5 月也专门发表了一篇关于 FHE 的文章，推荐感兴趣的朋友们阅读。

那么 FHE 到底是一门什么技术？

想要理解FHE 全同态加密这个拗口的名词，必须先理解什么是「加密」，什么是「同态」，以及为什么要「全」。

1. 什么是加密？

普通的加密大家最熟悉。举个例子，Alice 要发个口信给 Bob，比如要发个「1314 520」。

如果现在，既要第三方 C 来送信，又要做到信息保密，那么很简单——只需要将每个数字 x2 来加密，比如变成「2628 1040」即可。

当 Bob 收到后，将每个数字依次除 2，就解密出了原来 Alice 在说「1314 520」。

看到了么，两人通过对称加密，在既要雇 C 出力却又要 C 不知道信息的情况下，完成了信息传递。一般，谍战片里，两个联络员相互通信大抵不会超过这个范畴。

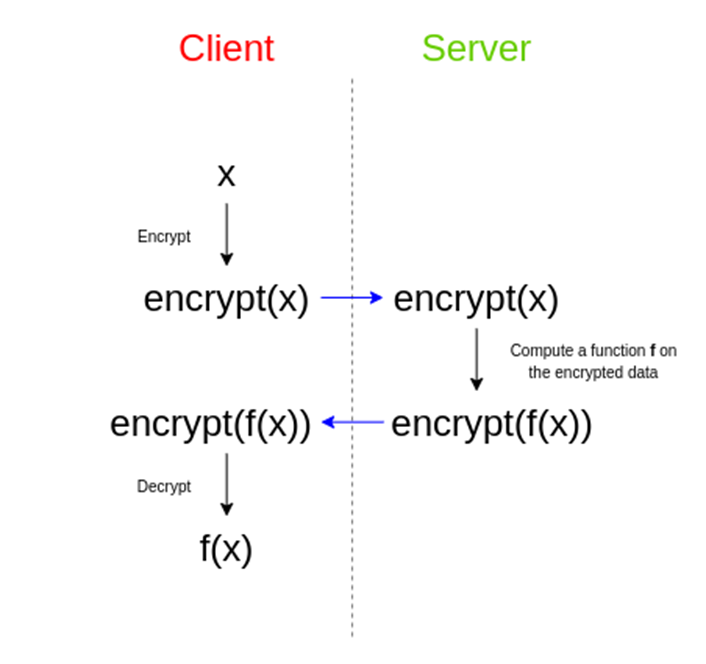
2. 那什么是同态加密呢？

现在 Alice 的需求难度升级了：

-比如 Alice 只有 7 岁；
-Alice 只会算 x2 和 ÷2 这样最简单的算术，其他运算则一概不懂。

好，那现在假设 Alice 要交电费了，Alice 家每月电费是 400 元，一共拖欠了 12 个月。

然而，400*12= 几，这道题目超过了年仅 7 岁的 Alice 的计算范围，她不会这么复杂的计算。

但是，她不想让别人知道她家电费多少钱 / 几个月，因为这是敏感信息。

因此，Alice 在不信任 C 的情况下，拜托 C 来帮忙计算。

因为她只会 x2 ÷2，因此她使用 x2 乘法给她的数字做了简单的加密，于是，她告诉 C，让 C 计算 800x24= 多少，即：（400x2）乘（12x2）。

C 是成年人，拥有强大的计算脑力，很快就口算出了 800*24=19200，并且把数字告诉了 Alice。然后，Alice 将结果，也就是 19200÷2÷2，很快就知道原来自己要缴纳 4800 元水费。

看到了么？这就是最简单的一个乘法同态加密，800*24 只是 400*12 的映射，变幻前后实际上形态是相同的，因此称之为「同态」。

这样的加密方式实现了：某人要委托一个不信任的实体计算结果，却能保证自己的敏感数字不泄露。

3. 那为什么「同态加密」还要「全」呢？

但是，刚刚只是理想世界里的问题，现实世界上的问题并没有这么简单，不是所有人都是 7 岁，或者都像 C 那么老实。

我们假设一种很坏的情况，比如 C 可能会尝试反推，C 通过穷举法也能破译出 Alice 要计算的是 400 和 12。

这时候，就需要「全同态加密」来解决。

Alice 给每个数字都×2，这个 2 可以视作一个噪声。噪声太少，就容易被 C 破解。

所以，Alice 可以在乘法基础上，再引入一道加法。

当然，最好这个噪声犹如早九点的主干道十字路口，那么 C 的破解难度就比登天还难。

所以，Alice 可以再乘 4 次，加 8 次，这样 C 破解概率就大幅降低了。

然而，这样 Alice 仍然只是「部分」同态加密，即：

（1）她加密内容只能针对特定部分问题；
（2）她只能使用特定部分运算法则，因为加法乘法次数不可太多（一般不能超过 15 次）。

而「全」的意思是说，要允许 Alice 针对一个多项式，能够做加法加密任意次，做乘法加密任意次，这样委托第三方完全计算，解密后还能得到正确结果。

一个超级长的多项式，几乎可以表达世界上绝大部分的数学问题，而不仅仅计算电费这种 7 岁小朋友的问题。

再加套上了任意次的加密，从根本上就几乎杜绝了 C 想要窥探隐私数据的可能性，真正实现了「既要又要」。

因此，「全同态加密」这门技术，一直是加密学圣杯上的一颗明珠。

事实上，同态加密这门技术一直到 2009 年之前，都只支持「部分同态加密」。

而 2009 年 Gentry 等学者提出的新思路，才打开了全同态加密可能性的大门。感兴趣的读者也可以移步这篇论文。

很多朋友对这门技术的应用场景，仍然抱有疑惑，什么场景会需要使用全同态加密 (FHE) 技术呢？

比如说——AI。

大家都知道，一个强悍的 AI 需要足够多的数据喂养，但偏偏很多数据的隐私价值又太高。那么能不能通过 FHE 实现这个问题的「既要又要」呢？

答案是可以的。

你可以：
（1）把你的敏感数据按照 FHE 方式进行加密；
（2）用加密后的数据交给 AI 计算；
（3）然后 AI 给你吐出一坨谁也看不懂的乱码。

非监督 AI 可以实现这一点，因为这些数据在它那里本质就是向量，AI 尤其是 GPT 这类生成型 AI，压根就不理解我们给它输入的话，只不过它通过向量「预测」出了最应该回答的话。

然而，由于这坨乱码遵循着某种数学规则，而你正是加密它的主人，那么：

（4）你大可以断开网络，在本地从容解密这些乱码，就像 Alice 一样；
（5）进而，你实现了：让 AI 对你的敏感数据完全不经手的条件下，运用庞大算力帮你完成了计算。

而现在的 AI 则做不到这点，必须放弃隐私才行，想想你明文输入给 GPT 的一切吧！要实现这个，非 FHE 不可。

这就是 AI 和 FHE 天生契合的根源，千言万语化成一个词：既要又要。

由于 FHE 和 AI 挂上了钩，横跨加密和 AI 两大领域，自然得到了额外的青睐，关于 FHE 的项目不少，比如 Zama, Privasea, Mind Network, Fhenix, Sunscreen 等等，FHE 应用的方向也各有创意。

今天拿其中一个项目 @Privasea_ai 出来做个解析。这是个 Binance 领投的 FHE 项目，它的白皮书描述了一个很贴切的场景，比如说人脸识别。

既要：机器算力能够判断此人是否为真人；

又要：机器不经手任何人脸敏感信息。

引入 FHE，能够有效解决这个难题。

然而，如果真要做现实世界的 FHE 计算，需要非常庞大的算力，毕竟 Alice 要做「任意次」的加法和乘法加密，无论是计算，加密、解密都是一个颇耗算力的过程。

因此，在 Privasea 要组建一个强大的算力网络，以及配套设施。因此，Privasea 又提出了一个类 PoW+类 PoS 网络的架构来解决这个算力网络的问题。

最近，Privasea 刚刚宣布了自己的 PoW 硬件，叫做 WorkHeart USB，这个可以理解为是 Privasea 的算力网络的配套设施之一，当然你可以简单理解它为一个矿机。

初始定价是 0.2 ETH，能够挖出网络的 6.66% 总代币。

以及还有一个类 PoS 资产，叫做 StarFuel NFT，这个可以理解为「工作证」，总量 5000 个。

初始定价也是 0.2 ETH，能够领到网络的 0.75% 总代币（通过空投）。

这个 NFT 也有点意思，它是类 PoS，但不是真 PoS，它在试图回避「PoS 在美国到底是不是证券」的问题。

这个 NFT 支持用户往里面抵押 Privasea 的代币，但是它不直接产生 PoS 收益，而是让你绑定的 USB 设备挖矿效率加倍，所以是个变相 PoS。

书归正传，如果 AI 真的能够大规模普及 FHE 技术，那么对于 AI 自己来说真的是个福音，要知道现在很多国家监管 AI 的重点都在数据安全和数据隐私。

甚至，举个不恰当的例子，比如俄乌战争里，一些俄国军方都在试图使用 AI，但是考虑到大量 AI 公司的美国背景，大概情报部门要被穿透得千疮百孔了。

但是如果不使用 AI，又自然会落后一大截。哪怕现在可能差距还不大，再给 10 年时间，也许我们都无法想象没有 AI 的世界了。

因此，数据隐私，大到两国战争冲突，小到手机人脸解锁，无处无存在于我们的生活。

而 AI 的时代，如果 FHE 技术能够真正成熟，那无疑是人类的最后一道防线。

原文链接