玩币族移动版

原文标题：《Exploring circle STARKs》撰文：Vitalik Buterin，以太坊联合创始人编译：Chris，Techub News

想要理解这篇文章的前提是你们已经了解了 SNARKs 和 STARKs 的基本原理。如果你对此不太熟悉，建议你先阅读本文的前几部分来了解相关基础知识。

近年来，STARKs 协议设计的趋势是转向使用较小的字段。最早期的 STARKs 生产实现使用的是 256 位字段，即对大数字（如 21888...95617）进行模运算，这使得这些协议与基于 elliptic curve 的签名兼容。但是这种设计的效率比较低，一般情况下，处理计算这些大数字并没有实际的用途，还会浪费很多的算力，比如处理 X（代表某个数字）和处理四倍的 X ，处理 X 只需要九分之一的计算时间。为了解决这个问题，STARKs 开始转向使用更小的字段：首先是?Goldilocks?，然后是?Mersenne31 和 BabyBear。

这种转变提升了证明速度，比如 Starkware 能够在一台 M3 笔记本电脑上每秒证明?620,000 个 Poseidon2 哈希值。这意味着，只要我们愿意信任 Poseidon2 作为哈希函数，那么就可以解决开发高效的?ZK-EVM?中的难题。那么这些技术是如何工作的？这些证明如何在较小的字段上建立？这些协议与 Binius 等解决方案相比如何？本文将探讨这些细节，特别关注一种名为?Circle STARKs（在?Starkware 的 stwo、Polygon 的?plonky3?以及我自己在 Python 中实现的版本）的方案，这种方案具有与 Mersenne31 字段兼容的独特属性。

使用较小的数学字段时常见的问题

在创建基于哈希的证明（或任何类型的证明）时，一个非常重要的技巧是通过对多项式在随机点的评估结果进行证明，能够间接验证多项式的性质。这种方法可以大大简化证明过程，因为在随机点的评估通常比处理整个多项式要容易得多。

例如，假设一个证明系统要求你生成一个对多项式的 commitment，A，必须满足 A^3 (x) + x - A (\omega*x) = x^N（ZK-SNARK 协议中一种非常常见的证明类型）。协议可以要求你选择一个随机坐标 ? 并证明 A (r) + r - A (\omega*r) = r^N。然后反推 A (r) = c，你证明了 Q = \frac {A - c}{X - r} 是一个多项式。

如果你事先了解了协议的细节或内部机制，你可能会找到方法绕过或破解这些协议。接下来可能会提到具体的操作或方法来实现这一点。比如，为了满足 A (\omega * r) 方程，你可以设置 A (r) 为 0，然后让 A 成为经过这两个点的直线。

为了防止这些攻击，我们需要在攻击者提供了 A 之后再选择 r（Fiat-Shamir?是一种用于增强协议安全性的技术，通过将某些参数设为某种哈希值来避免攻击。选择的参数需要来自一个足够大的集合，以确保攻击者无法预测或猜测这些参数，从而提高系统的安全性。

在基于 elliptic curve 的协议和 2019 年时期的 STARKs 中，这个问题很简单：我们所有的数学运算都在 256 位的数字上进行，因此我们可以将 r 选择为一个随机的 256 位数字，这样就可以了。然而，在较小字段上的 STARKs 中，我们遇到了一个问题：只有大约 20 亿种可能的 r 值可以选择，因此一个想要伪造证明的攻击者只需要尝试 20 亿次，虽然工作量很大，但对于一个下定决心的攻击者来说，还是完全可以做到的！

这个问题有两个解决方案：

进行多次随机检查

扩展字段

执行多次随机检查的方法是最简单有效的：与其在一个坐标上进行检查，不如在四个随机坐标上重复检查。这在理论上是可行的，但存在效率问题。如果你处理的是一个度数小于某个值的多项式，并且在某个大小的域上进行操作，攻击者实际上可以构造看起来在这些位置上都很正常的恶意多项式。因此，他们能否成功破坏协议是一个概率性问题，因此需要增加检查的轮数，以增强整体的安全性，确保能够有效防御攻击者的攻击。

这引出了另一个解决方案：扩展域，扩展域类似于复数，但它是基于有限域的。我们引入一个新的值，记作 α\alphaα，并声明其满足某种关系，比如 α2=some value\alpha^2 = \text {some value}α2=some value。通过这种方式，我们创建了一个新的数学结构，能够在有限域上进行更复杂的运算。在这种扩展域中，乘法的计算变为使用新值 α\alphaα 的乘法。我们现在可以在扩展的域中操作值对，而不仅仅是单个数字。比如，如果我们在 Mersenne 或 BabyBear 这样的字段上工作，这样的扩展允许我们有更多的值选择，从而提高安全性。为了进一步提高字段的大小，我们可以重复应用相同的技术。由于我们已经使用了 α\alphaα，所以我们需要定义一个新的值，这在 Mersenne31 中表现为选择 α\alphaα 使得 α2=some value\alpha^2 = \text {some value}α2=some value。

代码（你可以用?Karatsuba?改进它）

通过扩展域，我们现在有了足够多的值来选择，满足我们的安全需求。如果处理的是度数小于 ddd 的多项式，每轮可以提供 104 位的安全性。这意味着我们有足够的安全保障。如果需要达到更高的安全级别，比如 128 位，我们可以在协议中加入一些额外的计算工作，以增强安全性。

扩展域仅在 FRI（Fast Reed-Solomon Interactive）协议和其他需要随机线性组合的场景中实际使用。大部分的数学运算仍然在基础字段上进行，这些基础字段通常是模 ppp 或 qqq 的字段。同时，几乎所有哈希的数据都是在基础字段上进行的，因此每个值只需哈希四字节。这样做可以利用小字段的高效性，同时在需要进行安全性增强时，可以使用更大的字段。

Regular FRI

在构建 SNARK 或 STARK 时，第一步通常是 arithmetization 。这是将任意计算问题转化为一个方程，其中某些变量和系数是多项式。具体来说，这个方程通常会看起来像 P (X,Y,Z)=0P (X, Y, Z) = 0P (X,Y,Z)=0，其中 P 是一个多项式，X、Y 和 Z 是给定的参数，而求解器需要提供 X 和 Y 的值。一旦有了这样的方程，该方程的解就对应于底层计算问题的解。

要证明你有一个解，你需要证明你所提出的值确实是合理的多项式（而不是分数，或者在某些地方看起来像一个多项式，而在其他地方却是不同的多项式，等等），并且这些多项式具有一定的最大度数。为此，我们使用了一个逐步应用的随机线性组合技巧：

假设你有一个多项式 A 的评估值，你想证明它的度数小于 ?2^{20}

考虑多项式 B (x^2) = A (x) + A (-x)，C (x^2) = \frac {A (x) - A (-x)}{x}

D 是 B 和 C 的随机线性组合，即 D=B+rCD = B + rCD=B+rC，其中 r 是一个随机系数。

本质上，发生的事情是 B 隔离偶数系数 A，和?隔离奇数系数。给定 B 和 C，你可以恢复原始多项式 A：A (x) = B (x^2) + xC (x^2)。如果 A 的度数确实小于 2^{20}，那么 B 和 C 的度数将分别为 A 的度数和 A 的度数减去 1。因为偶次项和奇次项的组合不会增加度数。由于 D 是 B 和 C 的随机线性组合，D 的度数也应为 A 的度数，这使得你可以通过 D 的度数来验证 A 的度数是否符合要求。

首先，FRI 通过将证明多项式度数为 d 的问题简化为证明多项式度数为 ?d/2 的问题，从而简化了验证过程。这个过程可以重复多次，每次都将问题简化一半。

FRI?的工作原理是重复这个简化过程。例如，如果你从证明多项式的度数为 d 开始，通过一系列步骤，你将最终证明多项式的度数为 d/2。每次简化后，生成的多项式的度数逐步减小。如果某个阶段的输出不是预期的多项式度数，那么这一轮的检查将失败。如果有人试图通过这种技术推送一个不是度数为 d 的多项式，那么在第二轮输出中，其度数将有一定的概率不符合预期，第三轮中会更有可能出现不符合的情况，最终的检查将失败。这种设计可以有效地检测并拒绝不符合要求的输入。如果数据集在大多数位置上等于一个度数为 d 的多项式，这个数据集有可能通过 FRI 验证。然而，为了构造这样一个数据集，攻击者需要知道实际的多项式，因此即使有轻微缺陷的证明也表明证明者能够生成一个「真实」的证明。

让我们更详细地了解一下这里发生的情况，以及使这一切正常运作所需的属性。在每一步中，我们将多项式的次数减少一半，同时也将点集（我们关注的点的集合）减少一半。前者是使 FRI（Fast Reed-Solomon Interactive）协议能够正常工作的关键。后者则使得算法运行速度极快：由于每一轮的规模比上一轮减少一半，总的计算成本是 O (N)，而不是 O (N*log (N))。

为了实现域的逐步减少，使用了一个二对一映射，即每个点都映射到两个点中的一个。这种映射允许我们将数据集的大小减少一半。这个二对一映射的一个重要优点是它是可重复的。也就是说，当我们应用这个映射时，得到的结果集仍然保留了相同的属性。假设我们从一个乘法子群（multiplicative subgroup）开始。这个子群是一个集合 S，其中每个元素 x 都有其倍数 2x 也在集合中。如果对集合 S 进行平方操作（即将集合中的每个元素 x 映射到 x^2），新的集合 S^2 也会保留同样的属性。这种操作允许我们继续减少数据集的大小，直到最终只剩下一个值。虽然理论上我们可以将数据集缩小到只剩一个值，但在实际操作中，通常会在到达一个较小的集合之前就停止。

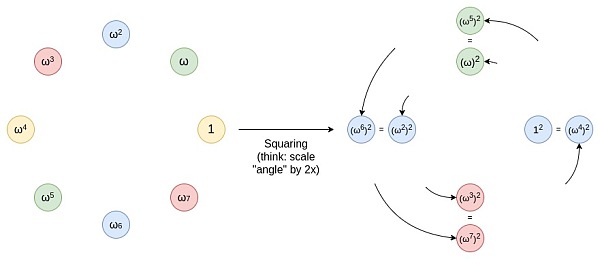
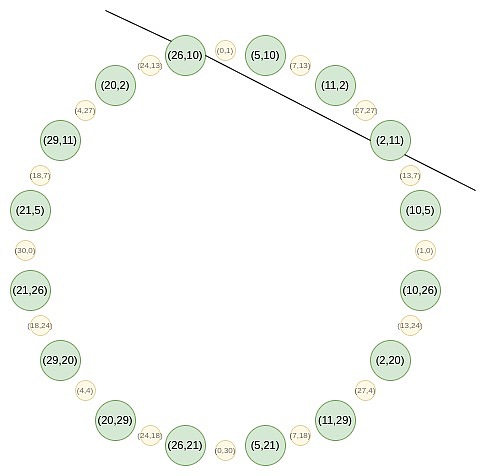
你可以将这个操作想象成一个将圆周上的一条线（例如，线段或弧）沿圆周伸展的过程，使它绕圆周旋转两圈。例如，如果一个点在圆周上位于 x 度的位置，那么在经过这个操作后，它会移动到 2x 度的位置。圆周上的每个点从 0 到 179 度的位置，都有一个对应的点在 180 到 359 度的位置，这两个点会重合。这意味着，当你将一个点从 x 度映射到 2x 度时，它会与一个位于 x+180 度的位置重合。这个过程是可以重复的。也就是说，你可以多次应用这个映射操作，每次都将圆周上的点移动到它们的新位置。

为了使映射技术有效，原始乘法子群的大小需要具有大的 2 的幂作为因子。BabyBear 是一个具有特定模数的系统，其模数为某个值，使得其最大乘法子群包含所有非零值，因此子群的大小为 2k?1（其中 k 是模数的位数）。这种大小的子群非常适合上述技术，因为它允许通过重复应用映射操作来有效地减少多项式的度数。在 BabyBear 中，你可以选择大小为 2^k 的子群（或者直接使用整个集合），然后应用 FRI 方法将多项式的度数逐步减少到 15，并在最后检查多项式的度数。这种方法利用了模数的性质和乘法子群的大小，使得计算过程非常高效。Mersenne31 是另一个系统，其模数为某个值，使得乘法子群的大小为 2^31 - 1。在这种情况下，乘法子群的大小只有一个 2 的幂作为因子，这使得它只能被除以 2 一次。之后的处理不再适用上述技术，也就是说，无法像 BabyBear 那样使用 FFT 进行有效的多项式度数减少。

Mersenne31 域非常适合在现有的 32 位 CPU/GPU 操作中进行算术运算。因为其模数的特性（例如 2^{31} - 1）使得很多运算可以利用高效的位操作来完成：如果两个数字相加的结果超过了模数，可以通过将结果与模数进行位移操作来减小到合适的范围。位移操作是一种非常高效的运算。乘法运算中，可以使用特定的 CPU 指令（通常称为高位位移指令）来处理结果。这些指令可以高效地计算乘法的高位部分，从而提高了运算的效率。在 Mersenne31 域中，由于上述特性，算术运算比在 BabyBear 域中快约 1.3 倍。Mersenne31 提供了更高的计算效率。如果可以在 Mersenne31 域中实现 FRI，这将显著提升计算效率，使得 FRI 的应用变得更加高效。

Circle FRI

这就是?Circle STARKs?的巧妙之处，给定一个质数 p，可以找到一个大小为 p 的群体，该群体具有类似的二对一特性。这个群体是由所有满足某些特定条件的点组成的，例如，x^2 mod p 等于某个特定值的点集。

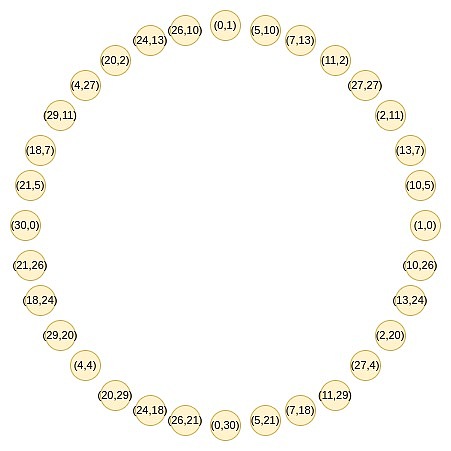
这些点遵循一种加法规律，如果你最近做过三角学或复数乘法的相关内容，你可能会觉得这种规律很熟悉。

(x_1, y_1) + (x_2, y_2) = (x_1x_2 - y_1y_2, x_1y_2 + x_2y_1)

双倍形式是：

2 * (x, y) = (2x^2 - 1, 2xy)

现在，让我们专注于这个圆上奇数位置上的点：

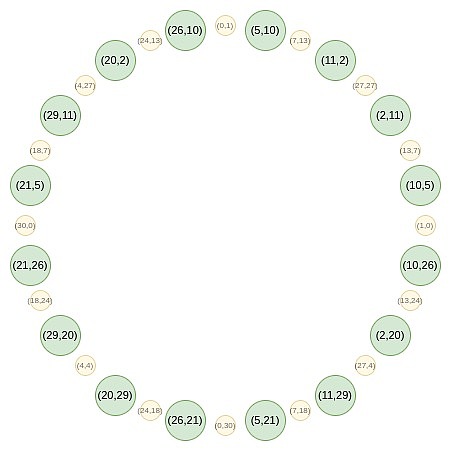
首先，我们将所有点收敛到一条直线上。我们在常规 FRI 中使用的 B (x?) 和 C (x?) 公式的等效形式是：

f_0 (x) = \frac {F (x,y) + F (x,-y)}{2}

然后，我们可以进行随机线性组合，得到一个一维的 P (x)，这个多项式在 x 线的一个子集上定义：

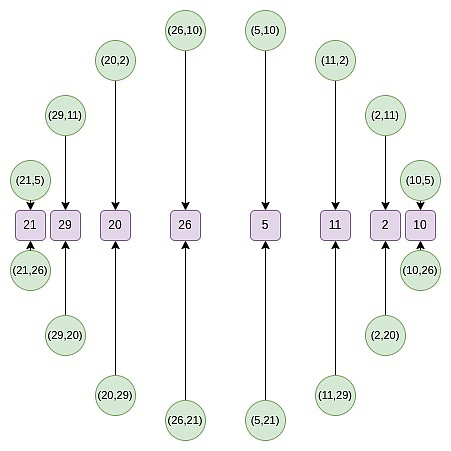
从第二轮开始，映射发生了变化：

f_0 (2x^2-1) = \frac {F (x) + F (-x)}{2}

这个映射实际上每次都将上述集合的大小减少一半，这里发生的事情是，每个 x 在某种意义上代表了两个点：(x, y) 和 (x, -y)。而 (x → 2x^2 - 1) 就是上面的点倍增法则。因此，我们将圆上两个相对点的 x 坐标，转换为倍增后的点的 x 坐标。

例如，如果我们取圆上第二个从右边数的值 2，并应用映射 2 → 2 (2^2) - 1 = 7，我们得到的结果是 7。如果我们回到原始圆上，(2, 11) 是从右边数第三个点，所以将其倍增后，我们得到的是从右边数第六个点，即 (7, 13)。

这本可以在二维空间中完成，但在一维空间中操作会使过程更高效。

Circle FFTs

一种与 FRI 密切相关的算法是?FFT，它将一个度小于 n ?的多项式的 n ?个评估值转换为该多项式的 ?n 个系数。FFT 的过程与 FRI 相似，不同之处在于，FFT 在每一步中不是生成随机线性组合 ?f_0 ?和 ?f_1 ，而是递归地对它们进行半大小的 FFT，并将 FFT (f_0) 的输出作为偶数系数，将 FFT (f_1) 的输出作为奇数系数。

Circle group 也支持 FFT，这种 FFT 的构造方式与 FRI 类似。然而，一个关键区别在于，Circle FFT（和 Circle FRI）所处理的对象并不严格是多项式。相反，它们是数学上称为?Riemann-Roch space?的东西：在这种情况下，多项式是模圆的 ( x^2 + y^2 - 1 = 0 ）。也就是说，我们将 x^2 + y^2 - 1 的任何倍数视为零。另一种理解方式是：我们只允许 ?y 的一次幂：一旦出现 ?y^2 项，我们就将其替换为 ?1 - x^2 。

这还意味着，Circle FFT 输出的系数并不像常规 FRI 那样是单项式（例如，如果常规 FRI 输出为 [6, 2, 8, 3]，那么我们知道这意味着 ?P (x) = 3x^3 + 8x^2 + 2x + 6 ）。相反，Circle FFT 的系数是特定于 Circle FFT 的基础：{1, y, x, xy, 2x^2 - 1, 2x^2y - y, 2x^3 - x, 2x^3y - xy, 8x^4 - 8x^2 + 1...}

好消息是，作为开发者，您几乎可以完全忽略这一点。STARKs 从不要求您了解系数。相反，您只需将多项式作为在特定域上的一组评估值进行存储。唯一需要使用 FFT 的地方是进行（Riemann-Roch 空间的类似）低度扩展：给定 N 个值，生成 k*N 个值，这些值都在同一多项式上。在这种情况下，您可以使用 FFT 生成系数，将（k-1) n 个零附加到这些系数上，然后使用逆 FFT 获取更大的评估值集。

Circle FFT 不是唯一的特殊 FFT 类型。?Elliptic curve?FFT 更为强大，因为它们可以在任何有限域（素数域、二进制域等）上工作。然而，ECFFT 更复杂且效率较低，因此由于我们可以在 ?p = 2^{31}-1 上使用 Circle FFT，所以我们选择使用它。

从这里开始，我们将深入一些更为晦涩的细节，实现 Circle STARKs 实现的细节与常规 STARKs 有所不同。

Quotienting

在 STARK 协议中，常见的一种操作是对特定点进行商运算，这些点可以是故意选择的，也可以是随机选择的。例如，如果你想证明 P (x)=y，可以通过以下步骤进行：

计算商：给定多项式 P (x) 和常数 y，计算商 Q ={P - y}/{X - x}，其中 X 是选择的点。

证明多项式：证明 Q 是一个多项式，而不是一个分数值。通过这种方式，证明了 P (x)=y 是成立的。

此外，在?DEEP-FRI 协议中，随机选择评估点是为了减少 Merkle 分支的数量，从而提高 FRI 协议的安全性和效率。

在处理 circle group 的 STARK 协议时，由于没有可以通过单一点的线性函数，需要采用不同的技巧来替代传统的商运算方法。这通常需要使用 circle group 特有的几何性质来设计新的算法。

在 circle group 中，你可以构造一个切线函数，使其在某个点 (P_x, P_y) 切于该点，但这个函数会通过该点具有重数 2，也就是说，要使一个多项式成为该线性函数的倍数，它必须满足比仅在该点为零更严格的条件。因此，你不能仅仅在一个点上证明评估结果。那么我们该如何处理呢？

我们不得不接受这个挑战，通过在两个点上进行评估来证明，从而添加一个我们不需要关注的虚拟点。

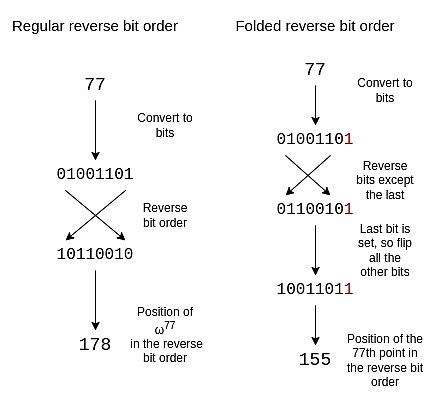
线函数：ax + by + c 。如果你把它变成一个方程，强制它等于 0，那么你可能会把它认出是高中数学中所谓的标准形式中的一条线。

如果我们有一个多项式 P 在 x_1 处等于 y_1，在 x_2 处等于 y_2，我们可以选择一个插值函数 L，它在 x_1 处等于 y_1，在 x_2 处等于 y_2。这可以简单地表示为 L = \frac {y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) + y_1。

然后我们证明 P 在 x_1 处等于 y_1，在 x_2 处等于 y_2，通过减去 L（使得 P - L 在这两个点上都为零），再通过 L（即 x_2 - x_1 之间的线性函数）除以 L 来证明商 Q 是一个多项式。

Vanishing polynomials

在 STARK 中，你试图证明的多项式方程通常看起来像是 C (P (x), P ({next}(x))) = Z (x) ? H (x) ，其中 Z (x) 是一个在整个原始评估域上都等于零的多项式。在常规 STARK 中，这个函数就是 ?x^n - 1 。在圆形 STARK 中，相应的函数是：

Z_1 (x,y) = y

Z_2 (x,y) = x

Z_{n+1}(x,y) = (2 * Z_n (x,y)^2) - 1

注意，你可以从折叠函数中推导出消失多项式：在常规 STARK 中，你重复使用 x → x^2 ，而在圆形 STARK 中，你重复使用 ?x → 2x^2 - 1 。不过，对于第一轮，你会进行不同的处理，因为第一轮是特殊的。

Reverse bit order

在 STARKs 中，多项式的评估通常不是按照 “自然” 顺序排列的（例如 P (1),P (ω),P (ω2),…,P (ωn?1)，而是按照我称之为逆位序（reverse bit order）的顺序排列的：

P (\omega^{\frac {3n}{8}})

如果我们设置 n=16，并且只关注我们在哪些 ω 的幂次上进行评估，那么列表看起来如下：

{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}

这种排序具有一个关键属性，即在 FRI 评估过程中早期分组在一起的值在排序中会相邻。例如，FRI 的第一步将 ?x 和 ?-x 分组。在 ?n = 16 ?的情况下，ω^8 = -1，这意味着 P (ω^i) ) 和 ( P (-ω^i) = P (ω^{i+8}) \)。正如我们所见，这些正是紧挨在一起的对。FRI 的第二步将 P (ω^i) 、 P (ω^{i+4}) 、P (ω^{i+8}) 和 P (ω^{i+12}) 分组。这些正是我们看到的四个一组的情况，以此类推。这样做使得 FRI 更加节省空间，因为它允许你为折叠在一起的值（或者，如果你一次折叠 ?k ?轮，则为所有 2^k 个值）提供一个 Merkle 证明。

在 circle STARKs 中，折叠结构略有不同：在第一步中，我们将 (x, y) 与 ?(x, -y) 配对；在第二步中，将 ?x 与 ?-x 配对；在随后的步骤中，将 ?p 与 q ?配对，选择 ?p ?和 ?q 使得 Q^i (p) = -Q^i (q)，其中 ?Q^i ?是重复 ?x → 2x^2-1 ?i 次的映射。如果我们从圆上的位置来考虑这些点，那么在每一步中，这看起来就像是第一个点与最后一个点配对，第二个点与倒数第二个点配对，依此类推。

为了调整反向位序以反映这种折叠结构，我们需要反转除了最后一位的每一位。我们保留最后一位，并用它来决定是否翻转其他位。

一个大小为 16 的折叠反向位序如下：

{0, 15, 8, 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}

如果你观察上一节中的圆，你会发现 0、15、8 和 7 这几个点（从右侧开始逆时针方向）是 (x, y)、(x, -y)、(-x, -y) 和 (-x, y) 的形式，这正是我们所需要的。

效率

在 Circle STARKs（以及一般的 31 位素数 STARKs）中，这些协议非常高效。一个在 Circle STARK 中被证明的计算通常涉及几种类型的计算：

1. 原生算术：用于业务逻辑，例如计数。

2. 原生算术：用于加密学，例如像?Poseidon?这样的哈希函数。

3.?查找参数：一种通用的高效计算方法，通过从表中读取值来实现各种计算。

效率的关键衡量标准是：在计算跟踪中，你是充分利用了整个空间来进行有用的工作，还是留下了大量的空闲空间。在大型字段的 SNARKs 中，往往存在大量的空闲空间：业务逻辑和查找表通常涉及对小数字的计算（这些数字往往小于 N，N 是一个计算步骤的总数，因此在实践中小于 2^{25}），但你仍然需要支付使用大小为 2^{256} 位字段的成本。在这里，字段的大小为 2^{31}，所以浪费的空间并不大。为 SNARKs 设计的低算术复杂度哈希（例如 Poseidon）在任何字段中都充分利用了跟踪中每个数字的每一位。

Binius 是比 Circle STARKs 更好的解决方案，因为它允许你混合不同大小的字段，从而实现更高效的位打包。Binius 还提供了在不增加查找表开销的情况下进行 32 位加法的选项。然而，这些优势的（在我看来）代价是会使概念变得更加复杂，而 Circle STARKs（以及基于 BabyBear 的常规 STARKs）在概念上则相对简单得多。

结论：我对 Circle STARKs 的看法

Circle STARKs ?对开发者来说并没有比 STARKs 复杂。在实现过程中，以上提到的三个问题基本上就是与常规 FRI 的区别。尽管 Circle FRI 操作的多项式背后的数学非常复杂，理解和欣赏这些数学需要一些时间，但这种复杂性实际上被隐藏得不那么显眼，开发者不会直接感受到。

理解 Circle FRI 和 Circle FFTs 也可以成为理解其他特殊 FFTs 的途径：最值得注意的是二进制域 FFTs，如?Binius?和之前的?LibSTARK?使用的 FFTs，还有一些更复杂的构造，如?elliptic curve FFTs, 这些 FFTs 使用少对多的映射，能够与 elliptic curve 点运算很好地结合。

结合 Mersenne31、BabyBear 和像 Binius 这样的二进制域技术，我们确实感觉我们正在接近 STARKs 基础层的效率极限。在这一点上，我预计 STARK 的优化方向将会有以下几个重点：

对哈希函数和签名等进行最大化效率的算术化：将哈希函数和数字签名等基本的密码学原语优化为最高效的形式，使其在 STARK 证明中使用时能够达到最佳性能。这意味着要针对这些原语进行专门的优化，以减少计算量和提高效率。

进行递归构造以启用更多并行化：递归构造指的是将 STARK 证明过程递归地应用于不同的层级，从而提高并行处理能力。通过这种方式，可以更高效地利用计算资源，加速证明过程。

算术化虚拟机以改善开发者体验：对虚拟机进行算术化处理，使得开发者在创建和运行计算任务时可以更加高效、简单。这包括对虚拟机进行优化，以便于在 STARK 证明中使用，改善开发者在构建和测试智能合约或其他计算任务时的体验。

查看更多